Bonjour,
Soit une surface chargée (densité surfacique de charge ) et un point M appartenant à cette surface. L'existence de charges électriques en M fait que le vecteur champ électrique en M n'est pas défini.
Soit la normale à la surface chargée passant par le point M.
Soit un point M1 sur cette normale, infiniment près de M mais situé dans le milieu n° 1.
Soit un point M2 sur cette normale, infiniment près de M mais situé dans le milieu n° 2.
On définit deux vecteurs unitaires, un normal à la surface, l'autre tangent à la surface de façon que le vecteur champ en M1 puisse s'écrire :

Le vecteur champ en M2 peut s'écrire :

En utilisant les propriétés de la divergence et du rotationnel du vecteur champ , on peut démontrer :
1° la continuité de la composante tangentielle du vecteur champ :

2° la discontinuité de la composante normale du vecteur champ :

Cela peut éventuellement se résumer par une seule formule vectorielle :

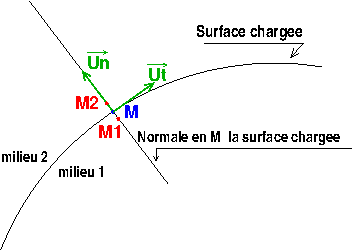
J'ai oublié le schéma correspondant à mon message précédent. Le voici avec, pour plus de clarté, un effet de "zoom" au voisinage du point M.

j'ai rien à dire vraiment merci de mon cœur