Niveau licence

Chainette et dérivée partielle

Posté par
Abcd78 17-12-17 à 14:31

Bonjour,
Je dois utiliser la notion de différentiellement pour résoudre la forme d'un câble suspendu entre 2 points. On considère un petit élément de longueur l du câble. La masse de cette élément est m = pl où p est la masse par unité de longueur du câble. Cette portion de cable est soumise à son poids et aux forces de tension T1 et T2 à ses extrémités.

Schéma :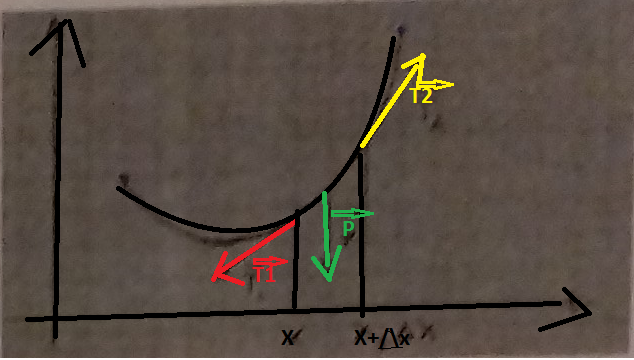
Chainette et dérivée partielle

Questions :
1) Appliquer le PFD à une portion de cable. En déduire que T1x + T2x = 0
T1y+T2y-mg=0

2) La tension est tangente au cable. On peut donc assimiler les pentes pour des portions suffisamment petites : Ty/TX = y/x que l'on notera f'(x). Établir qu'alors :
T1x = -T2x = T
Tf'(x+x)-Tf'(x)=pgl/x= $\sqrt{1+\frac{\Delta y}{\Delta x}^{2}$

3) Faire apparaître les formes dérivés par passage à la limite quand x tend vers 0
Tf"(x)=pg $\sqrt{1+f'²(x)}$

4) Poser h(x)=f'(x)=df/dx et résoudre la forme de la chaînette les conditions aux limites sont f'(0) = h(0) (la corde est horizontale au centre) et y(0) = 0 (centre du cable pris comme origine du repère).

Ce que j'ai fais :
** images supprimées => tu as tous les outils pour recopier ta proposition **

C?est surtout le f'(x+x) et le l qui me bloquent
et si vous aviez quelques indices pour les 2 dernières questions..

Merci d'avance

Posté par re : Chainette et dérivée partielle 17-12-17 à 14:55

Bonjour
Suggestion :
1° : commencer par étudier la démonstration que tu trouveras paragraphe 3 ici :

2° : poser ici des questions complémentaires si la démonstration ne te parait pas claire.

Posté par re : Chainette et dérivée partielle 17-12-17 à 21:56

Bonjour, merci pour ta réponse, j'ai réussi à rassembler plusieurs données à partir du lien donné pour résoudre la question 2 et 3 mais je n'ai vraiment aucune idée pour la question 4.

Voici ce que j'ai fais :

- PFD : T1+T2+P=0 à l'équilibre
On a T1 =T(x), T2=T(x+Δx) et P=pΔlg

On a donc T(x)+T(x+Δx)-pΔlg=0

- Projection : Selon l'axe vertical v : Tv(x+Δx)-Tv(x)=0
Selon l'axe horizontal h : Th(x+Δx)-Th(x)-P=0

On a alors Th=Th(x+Δx)-Th(x) et Tv=Tv(x+Δx)-Tv(x)

- Δl²=Δx²+Δy² d'après Pythagore et en considérant Δl la longueur infinétésimal de la chaine rectiligne.
Donc Δl= $\sqrt{\Delta x²+\Delta y²}$ et $\frac{\Delta l}{\Delta x}=\sqrt{1+(\frac{\Delta y}{\Delta x})²}$

- Ty/Tx = Δt/Δx=f'(x)

- T=Tv

Par contre je ne trouve pas à quoi correspond f'(x+Δx)

Posté par re : Chainette et dérivée partielle 17-12-17 à 22:09

Tout est démontré pas à pas sur le document fourni. Etudie en détail la partie 3 puis explique ce que tu ne comprends pas sur ce document.

Posté par re : Chainette et dérivée partielle 17-12-17 à 22:22

Alors pour la question 2 :
- Je ne comprend pas pourquoi Tf'(x+Δx)=Tv(x+Δx)/dx et pourquoi Tf'(x)=Tv(x)/dx
- Je ne comprend pas aussi pourquoi je dois trouver $\sqrt{1+(\frac{\Delta x}{\Delta y})²}$ alors que sur le document on trouve pg\sqrt{1+(\frac{\Delta x}{\Delta y})²}

Pour la question 3 :
- Je ne comprend pas pourquoi quand Δx tend vers 0 dx/dy tend vers dx/dy

Posté par re : Chainette et dérivée partielle 18-12-17 à 19:41

Bonsoir
Je reprends le début de la démonstration avec toi en notant T_v(x) et T_h(x) les valeurs absolues des projections du vecteur T sur l'axe vertical et l'axe horizontal. Je me demande si tu n'a pas permuté v et h dans certaines formules. Relation fondamentale de la statique projetée sur l'axe horizontal :

$T_{h}(x)=T_{h}(x+\Delta x )$
Projection sur l'axe vertical :

$T_{v}(x)+\rho.g.\Delta l=T_{v}(x+\Delta x)$

$T_{v}(x+\Delta x)-T_{v}(x)=\rho.g.\Delta x.\sqrt{1+\left(\frac{\Delta y}{\Delta x}\right)^{2}}$

$\frac{T_{v}(x+\Delta x)-T_{v}(x)}{\Delta x}=\rho.g.\sqrt{1+\left(\frac{\Delta y}{\Delta x}\right)^{2}}$

On pose : y=f(x) : équation (encore inconnue de la chaînette). Passage à la dérivée en supposant $\Delta x$ très petit :

$\frac{dT_{v}}{dx}=\rho.g.\sqrt{1+f'(x)^{2}}$
Tu as surement en tête la définition de la dérivée d'une fonction x T(x) par rapport à x :

$\frac{dT}{dx}=\lim_{\Delta x\rightarrow0}\left(\frac{T(x+\Delta x)-T(x)}{\Delta x}\right)$
Je te laisse continuer...