Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... AutreForum autre de supérieur PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau autre
Partager :

centre de poussée

Posté par
Ariel60 07-10-16 à 21:21

Bonjour,
On considere un flotteur spherique homogene de rayon R placé sur l'eau.Son centre O se trouve à R/2 de la surface libre.Pour des deplacements isocarenes,déterminer:
1)la surface enveloppee par le plan de flottaison
2)la position du centre de poussee C

Pour la 1),est-ce qu'il s'agit d'un disque de centre O et de rayon R??
Pour la 2),je ne comprends pas d'où vient l'expression:OC=\int \int \int \frac{z dV}{V}
Merci d'avance

Posté par
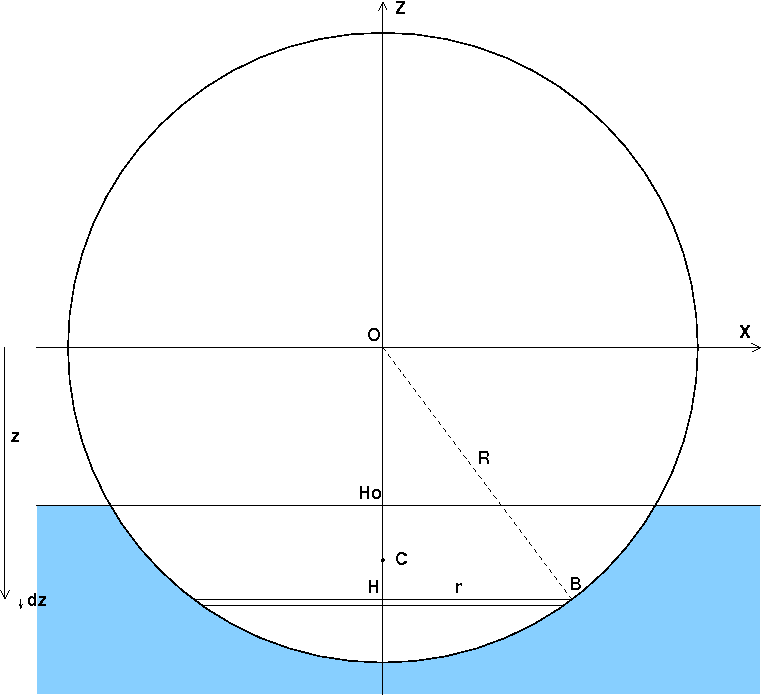
vanoisere : centre de poussée 07-10-16 à 21:56

Sans schéma, je ne suis pas sûr t'avoir bien imaginé la situation. D'après ce que  je comprends, la ligne de flottaison est un cercle dont le centre est sur la verticale passant par le centre du flotteur et dont le rayon est donné par le théorème de Pythagore :

R_{f}=\sqrt{R^{2}-\frac{R^{2}}{4}}=R.\frac{\sqrt{3}}{2}
  L'aire du disque délimité par la ligne de flottaison est ainsi :

S_{f}=\pi R_{f}^{2}=\frac{3}{4}\pi R^{2}
Le centre de poussée est le centre de gravité de la carène en supposant celle-ci entièrement composée d'eau. Tu as surement étudié en cours les expressions des coordonnée du centre d'inertie (ou centre de gravité) d'un corps homogène. Tu obtiens la formule fournie...

Posté par
vanoisere : centre de poussée 08-10-16 à 15:19

Bonjour
Quelques compléments à mon message précédent :
1° tu parles de centre O de la sphère à la distance R/2 du plan de flottaison ; faut-il comprendre que le flotteur est immergé des trois quarts de sa hauteur ou seulement du quart ? Ta phrase est valide dans les deux cas et sans schéma...
2° La cote du centre C de poussée (en prenant l'origine z = 0 en 0) est donnée par la relation :
z_{C}=\frac{\iiint z\cdot dV}{\iiint dV}
Ce n'est pas exactement ce que tu as écrit...
3° tu as demandé de l'aide en thermo le  01-10-16 à 19:17. Je t'ai répondu de façon assez détaillée. Pas le moindre retour pour dire si cette aide a été utile...

Posté par
Ariel60re : centre de poussée 08-10-16 à 18:47

Bonjour,
Le centre O de la sphère est à l'air libre,seul un quart du flotteur est immergé.Je ne comprends pas d'où vient exactement l'expression de Zc.Je m'excuse de ne pas avoir répondu pour la question en thermo,mais ça m'a vraiment été utile,merci encore

Posté par
vanoisere : centre de poussée 08-10-16 à 19:02

Es-tu capable d'exprimer les coordonnées du centre de masse (centre d'inertie ou centre de gravité) G d'un solide homogène ? L'expression en découle directement.

Posté par
vanoisere : centre de poussée 08-10-16 à 21:25

Quelques précisions sur les coordonnées du centre d'inertie, confondu avec le centre de gravité dans la mesure où le champ de pesanteur est uniforme. Commençons pas le cas le plus simple : celui d'un système constitué de N masses ponctuelles m1, m1,... situées aux points A1,A2... La masse totale du système est : M=m_{1}+m_{2}+...=\sum_{i=1}^{i=N}m_{i} .
Le centre d'inertie G du système est le barycentre des différents points, chaque point étant affecté d'un coefficient égal à sa masse :

\overrightarrow{OG}=\frac{\sum_{i=1}^{i=N}m_{i}\cdot\overrightarrow{OA_{i}}}{M}
Supposons maintenant le système constitué d'un solide, donc d'une distribution continue de matière. On découpe alors le solide en une succession de volumes élémentaires, chaque volume élémentaire dV ayant une masse élémentaire dm=\rho\cdot dV  ; on note A un point quelconque du solide entouré d'un volume élémentaire dV, les coordonnées de A sont (x,y,z); \rho  est la masse volumique du solide au point A. Pour obtenir la position du centre d'inertie, on reprend la formule précédente en remplaçant les sommes discrètes par deux intégrales :

\overrightarrow{OG}=\frac{\iiint\overrightarrow{OA}\cdot\rho\cdot dV}{\iiint\rho\cdot dV}
Chaque intégrale triple est étendue à tout le solide. Si le solide est homogène, la masse volumique est une constante qui se simplifie dans le calcul. En notant ZG la cote de G :

\overrightarrow{OG}=\frac{\iiint\overrightarrow{OA}\cdot dV}{\iiint dV}\quad;\quad Z_{G}=\frac{\iiint z\cdot dV}{\iiint dV}
Ici, le centre de poussée C est le centre d'inertie de la partie de la sphère en-dessous du plan de flottaison, la carène étant supposée être de l'eau, donc constituant un système homogène. Par raison de symétrie, C appartient à l'axe Oz.

Z_{C}=\frac{\iiint z\cdot dV}{\iiint dV}=\frac{\iiint z\cdot dV}{V_{c}}
Les intégrales sont a priori triples mais il est facile de se ramener à deux intégrales simples. Je commence par calculer le volume Vc de la carène. Pour cela, on découpe celle-ci en tranches élémentaires de cotes z et d'épaisseurs élémentaires dz. Chaque tranche est un petit cylindre d'axe de symétrie Oz, de hauteur dz et de rayon r donné par le théorème de Pythagore :
\\ r^{2}=R^{2}-z^{2}
Le volume élémentaire de ce cylindre est ainsi : dV=\pi.r^{2}.dz=\pi\cdot\left(R^{2}-z^{2}\right)\cdot dz

V_{c}=\intop_{-R}^{\frac{-R}{2}}\pi\cdot\left(R^{2}-z^{2}\right)\cdot dz=\pi\left[R^{2}\cdot z-\frac{z^{3}}{3}\right]_{-R}^{\frac{-R}{2}}=\frac{5}{24}\cdot\pi\cdot R^{3}

\iiint z\cdot dV=\intop_{-R}^{\frac{-R}{2}}\pi\cdot\left(R^{2}\cdot z-z^{3}\right)\cdot dz=\pi\left[R^{2}\cdot\frac{z^{2}}{2}-\frac{z^{4}}{4}\right]_{-R}^{\frac{-R}{2}}=-\frac{9}{64}\cdot\pi\cdot R^{4}

On en déduit la cote du centre de poussée :

Z_{C}=\frac{-\frac{9}{64}\cdot\pi\cdot R^{4}}{\frac{5}{24}\cdot\pi\cdot R^{3}}\quad;\quad\boxed{Z_{C}=-\frac{27}{40}R}
Le centre de poussée est donc en-dessous du centre O du flotteur (puisque Zc<0), à la distance OC=\frac{27}{40}R  de ce centre O.

Posté par
vanoisere : centre de poussée 08-10-16 à 21:48

J'ai oublié le schéma dans mon message précédent. Le voici.

centre de poussée

Posté par
J-Pre : centre de poussée 09-10-16 à 10:09

L'énoncé aurait été plus précis s'il avait mentionné que O était au dessus ou en dessous de la "surface libre".

Posté par
vanoisere : centre de poussée 09-10-16 à 10:24

Citation :
L'énoncé aurait été plus précis s'il avait mentionné que O était au dessus ou en dessous de la "surface libre".

Cela au moins : c'est un scoop  constructif !
Mon message du 08-10-16 à 15:19
Citation :
1° tu parles de centre O de la sphère à la distance R/2 du plan de flottaison ; faut-il comprendre que le flotteur est immergé des trois quarts de sa hauteur ou seulement du quart ? Ta phrase est valide dans les deux cas et sans schéma...

La réponse d'Ariel60 du  08-10-16 à 18:47
Citation :
Le centre O de la sphère est à l'air libre,seul un quart du flotteur est immergé.

Posté par
J-Pre : centre de poussée 09-10-16 à 15:04

Et bien voila.

Inclure l'info. dans l'énoncé initial aurait cependant été mieux.

Posté par
Ariel60re : centre de poussée 10-10-16 à 17:04

Merci infiniment vanoise pour ces explications!Par contre mon corrigé dit dans 1) que la surface de flottaison enveloppee par le plan est une sphère de centre O et de rayon R/2,mais je ne vois pas comment?je pensai que ça devrait etre un disque

Posté par
vanoisere : centre de poussée 10-10-16 à 19:15

Bonsoir
La surface dont j'ai calculé l'aire précédemment est la surface de flottaison , c'est à dire le disque délimité par la ligne de flottaison.
J'ai mal lu l'énoncé : ce n'est pas cela qui est demandé mais la surface enveloppée par le plan de flottaison.
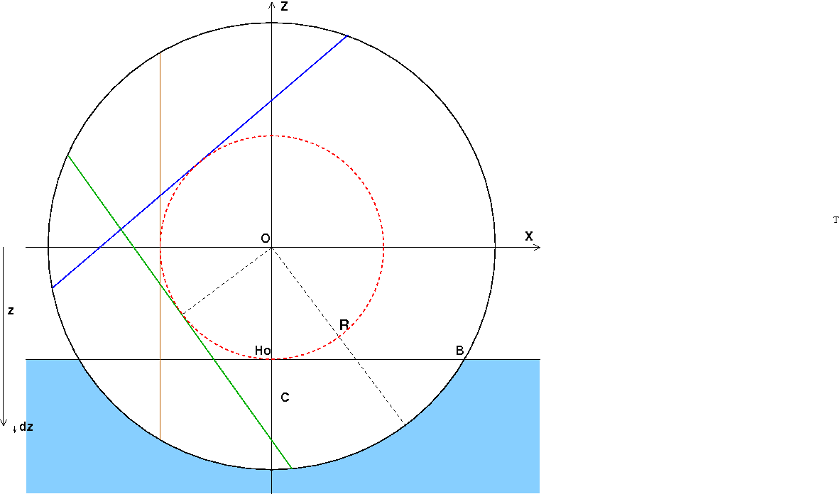
Lorsque le flotteur se déplace de façon isocarène, ce qui dans le cas d'un flotteur sphérique, revient à  imaginer le flotteur tournant sur lui-même autour de son centre O à distance fixe du plan de flottaison, la surface de flottaison ( le disque de centre Ho et de rayon Rf)  reste constamment tangente à la sphère de centre O et de rayon OH_0=\frac{R}{2} (sur mon schéma ci-dessus). Cette surface est aussi appelée surface enveloppe des flottaisons...
Toutes mes excuses pour cette faute d'inattention.
Pour plus de clarté regarde le schéma ci-dessous. Suppose le disque de flottaison de centre Ho fixe par rapport au flotteur. Si le flotteur tourne autour d'un axe perpendiculaire au plan de figure passant par O de 45° dans le sens horaire, ce disque a pour trace dans le plan de figure le segment tracé en vert ; après rotation d'un quart de tour, ce disque a pour trace le segment tracé en marron, après rotation de  135°, ce segment a pour trace le segment tracé en bleu... Je crois bien que cette surface enveloppe intervient dans l'étude de la stabilité des navires...

centre de poussée

Posté par
Ariel60re : centre de poussée 13-10-16 à 09:03

Et alors dans le cas où le flotteur n'est pas sphérique faut il toujours le faire tourner pour trouver la surface enveloppée?
Merci

Posté par
vanoisere : centre de poussée 13-10-16 à 10:23

Oui mais alors : cette surface n'est pas simple !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !