Niveau maths sup

Centre de gravité

Posté par
shana15 08-05-20 à 14:12

Bonjour,

voici l'énoncé :
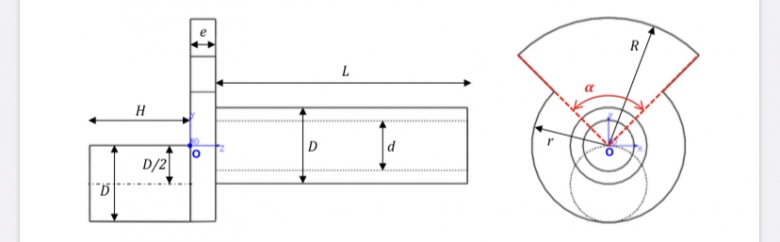
Soit un contrepoids composé d'un cylindre plein d'axe (O,z) d'épaisseur e, de rayon r auquel on ajoute un secteur cylindrique d'axe (O,z), d'angle d'ouverture , de même épaisseur e, de rayon intérieur r et de rayon extérieur R. Ce secteur est disposé symétriquement de part et d'autre de l'axe (O,y).

Je dois déterminer le centre de gravité de ce contrepoids.
J'ai déjà trouvé que le centre de gravité du cylindre plein est tq OGc = (e/2)z et que la composante sur z de la portion de secteur est également e/2.

Je n'arrive pas à déterminer la composante sur y du secteur (et donc du contrepoids). J'ai essayé la formule m(secteur)*yg=intégrale de OP.y*dm
mais les applications numériques ne sont pas concluantes.

Aire secteur = (R²-r²)/2
Pouvez-vous m'aider ?

Merci d'avance.

Posté par re : Centre de gravité 08-05-20 à 14:14

Bonjour
Il serait préférable de scanner et de poster ici un schéma propre du dispositif pour bien fixer les notations.

Posté par re : Centre de gravité 08-05-20 à 14:20

Bonjour à vous deux,

@shana15 : pourrais-tu mettre à jour ton niveau scolaire dans ton profil (il affiche toujours terminale) pour qu'on puisse adapter le discours à ton niveau réel ?

Posté par re : Centre de gravité 08-05-20 à 14:24

A ce que je peux comprendre sans schéma, tu pourrais sans doute commencer par t'intéresser à la masse dm de matière comprise entre les cylindres de rayon et +d avec compris entre r et R. Tu peux exprimer dm en fonction de , ,e,d et µ la masse volumique du métal. Applique alors la formule donnant la position du centre d'inertie de ce secteur cylindrique.
Sous toute réserve en attendant le schéma...

Posté par re : Centre de gravité 10-05-20 à 08:11

Voilà le schéma :

Centre de gravité

Posté par re : Centre de gravité 10-05-20 à 11:28

Pour des raison de symétrie, le centre d'inertie G1 du contrepoids est sur l'axe (Oy). La formule générale donnant l'ordonnée de G' est :

$m'.y_{G'}=\iiint y.dm$
Mon premier message donnait ma méthode pour obtenir m' mais il est possible ici de l'obtenir sans calcul puisque l'aire S' du secteur est fournie. En notant µ la masse volumique :

$m'=\mu.V=\mu.e.S'=\mu.e\cdot\dfrac{\alpha.\left(R^{2}-r^{2}\right)}{2}$
La masse dm peut s'écrire : dm=µ.e.dS
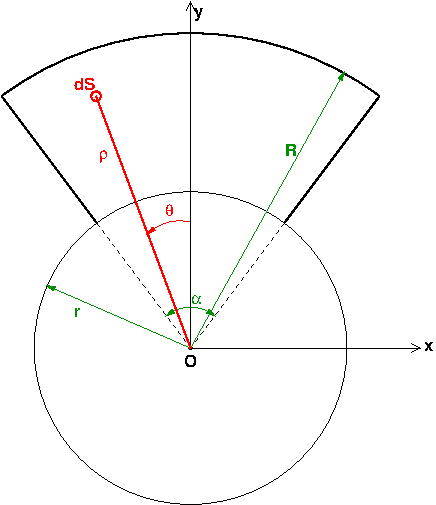
Le plus simple consiste à travailler en coordonnées polaires (voir schéma ci-dessous) :

$dS=\rho.d\theta.d\rho\quad;\quad y=\rho.\cos\left(\theta\right)\quad;\quad dm=\mu.e.\rho.d\theta.d\rho$

Donc, en séparant les variables de l'intégrale :

$\mu.e\cdot\frac{\alpha.\left(R^{2}-r^{2}\right)}{2}\cdot y_{G'}=\mu.e.\int_{-\frac{\alpha}{2}}^{\frac{\alpha}{2}}\cos\left(\theta\right).d\theta\cdot\int_{r}^{R}\rho^{2}.d\rho$

Je te laisse continuer...

Centre de gravité

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Centre de gravité

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique