Inscription / Connexion Nouveau Sujet
centre de gravité
bonjour tout le monde ,
je vous prie de bien vouloir me corriger cet exercice....merci d'avance.
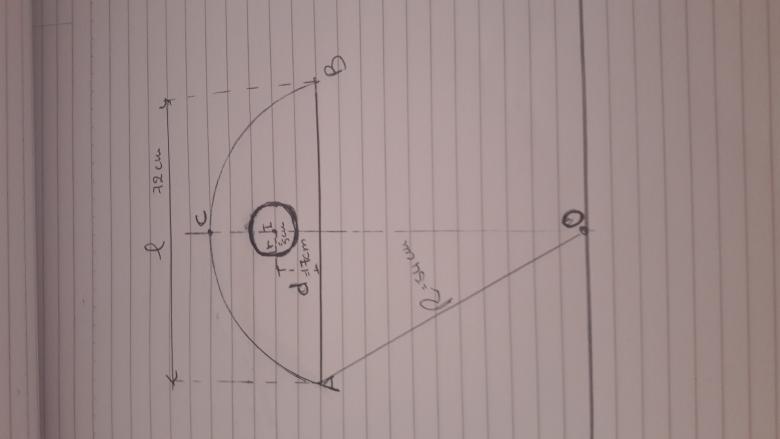
On considère un segment circulaire de centre O, de rayon R et dont la longueur de la corde AB et l. On perce un trou de rayon r dont le centre l se trouve sur l'axe de symétrie OC du segment AB à une distance d de la corde AB.
1. Déterminer la position OG1 du centre de gravité G1 du segment circulaire plein.
2. Déterminer la position OG du centre de gravité G du segment circulaire percé.
3. Application numérique : R= 54 cm, l= AB =72cm , r= 5 cm et d= 7cm.
Soit :
G1 le centre de gravité du segment pleine
G le centre de gravité du segment circulaire percé.
G est en I
R le rayon du cercle
θ l'angle AOB ;
Le centre de gravité d'un segment circulaire est situé sur le rayon qui passe par le milieu de l'arc à une distance du centre qu'est le quotient du cube de la corde par douze fois l'aire du segment.
Soit le segment ACB son centre de gravité G appartient au rayon OC qui passe par le milieu de l'arc, car cette ligne est un axe de symétrie pour le segment.
Pour obtenir la distance OG , nous considérons le secteur OACB comme la somme du segment et du triangle OAG, et nous appliquons le théorème des moments par rapport au plan perpendiculaire au point O de OC , pour déduire au final :
X G 1 = 0
OG1 = ( AB^3)/(12 A)
Avec A= l'aire du segment=
A= R²/2 (θ-sin〖θ)〗
X G = 0
OG = (- π OI r²) / ( R²/2 (θ-sinθ) - πr²)
Dans un cercle, la droite qui joint le milieu d'une corde au centre du cercle est la médiatrice de cette corde.
Cercle de centre O.
I milieu de la corde AB.
En effet, (OI), médiane du triangle isocèle OAB, est aussi la médiatrice de [AB].
OI = √(〖OA〗^2+〖OB/2 ²〗^ ) + d
cosθ=((OA^2+OB^2-AB^2 ))/(2(OA*OB))
Bonjour
En notant m la masse du secteur circulaire plein de centre de gravité G1, en notant md la masse du disque de centre I et de rayon r, le secteur circulaire troué à une masse (m-md) et un centre de gravité G.
Il suffit d'écrire que le centre de gravité G1 du secteur circulaire plein est le barycentre des points G et I :
On suppose qu'il s'agit une plaque homogène d'épaisseur constante ; la masse est alors proportionnelle à l'aire de la surface. En notant S l'aire du secteur circulaire plein, on obtient :
Les difficultés réelles résident dans les expressions de OG1 et de S mais apparemment tu as un formulaire. Sinon, tu as les démonstrations ici :
merci vanoise.....donc pour déterminer OG1 on applique le formulaire :
3R/3 x cos 3a/ 
-2a-sin2a
et
A = ½R2(â - sin â)??
Ton formulaire me semble correct mais effectivement, tu peux utiliser les formules que je t'ai fournies en remarquant :
2â=
As-tu bien compris le raisonnement qui m'as permis d'aboutir à OG ? C'est un "grand classique" !
oui j 'ai compris ton raisonnement qui t'as permis d'aboutir à OG
effectivement il peut être utile d'exprimer les calculs en fonction du demi-angle au centre du secteur circulaire
bonsoir vanoise ..désolée pour le retard..
finalement j'ai trouvé comme solution :
G1 le centre de gravite OG1 du segment circulaire plein se trouve sur l'axe de sa symétrie de ce segment, donc il suffit de déterminer la distance OG qu'est donnée par :
OG1=M/S
M=le moment statique = (2R3 sin3 â ) /3
S=l'air du segment circulaire plein=R²/2(sin2â -2â )
donc
OG1= ( (2R3 sin3 â ) /3) / R²/2(sin2â -2â )
Si tu peux vérifier stp.
Merci beaucoup vanoise
Bonsoir
En utilisant le formulaire que je t'ai fourni et en remarquant
-2
= :
Tu obtiens en remarquant :
Bonjour,
pouvez vous me vérifier ces calculs s'il vous plait, je vous remercie d'avance.
Application numérique : R= 54 cm, l= AB =72cm , r= 5 cm et d= 7cm.
α = arc sin(l/2R)= arc sin(72/2(54))
α = 42°
OG1= 4R/3 x ((sin a ^3) /( 2a-sin2 a ))
216/3 x ( 0.30/83) = 0.26
OG = 2/3 x ( (2R^3+ sin^3 a - 3π^2 (Rcosa+ d))) / (R²(2a-sin2a )-2πr²) ) )
OG = 2/3 x ((2*54)〗^3+ sin^3 42° -3π^2 (54cos42°+ 7))/ (54²(2*42°-sin2*42°)-2π5²) ) )= 0.87
*** message déplacé ***
Bonsoir
Il s'agit bien de l'application numérique de ton topic précédent sur le secteur circulaire? Si oui, il fallait poursuivre au lieu de créer un nouveau topic. J'ai fait le calcul mais il est sur mon bureau chez moi. Je suis en déplacement et je réponds ici avec un simple téléphone portable. Je peux te le poster mercredi soir mais si un autre aidant a le temps de prendre le relais avant : pas de probleme.
*** message déplacé ***
merci vanoise ...ok pas de problème ça peut attendre ....je te souhaite bon courage ..
sinon effectivement il s'agit de l'application numérique de mon topic précédent sur le secteur circulaire..mais je ne savais pas que j'ai le droit de revenir en arrière 
..mais là j'ai compris et cela ne se reproduira plus..
*** message déplacé ***
Bonsoir nano 21,
Je n'ai pas fait les calculs et ce qui suit n'est donc que des remarques à prendre avec précaution :
a)Tu écris :
OG1= 4R/3 x ((sin a ^3) /( 2a-sin2 a ))
et tu utilises pour ton calcul numérique un angle exprimé en degré, alors qu'il faut l'exprimer en radians.
et tu fais plusieurs fois la même erreur dans la suite.
b) Tu trouves finalement OG = 0,87 ( sans unité mais on présume que ce sont des cm )
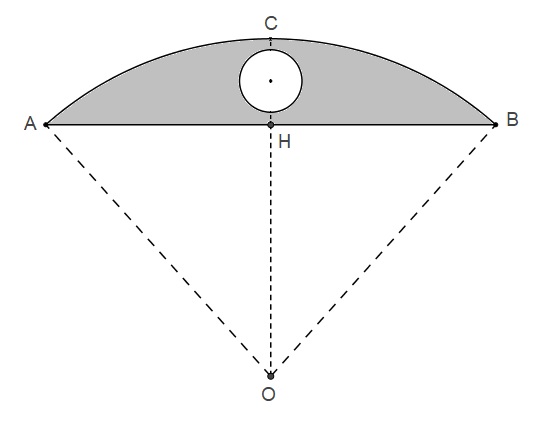
Si j'ai bien compris le problème, il me semble que le point G doit se trouver à l'intérieur du secteur circulaire et donc que G doit être situé entre H et C donc OG entre 40,2 cm et 54 cm
Bonsoir
Chose promise...
Remarque préliminaire : tu as choisi de régler ta calculatrice en mode "degrés" : très bien mais attention : lorsqu'une formule de longueur ou d'aire fait intervenir un angle, celui-ci doit être exprimé en radian. Exemple simple : la longueur de l'arc AB vaut : à condition que
soit exprimé en radian ; prends le cas particulier du cercle de rayon R : son périmètre vaut et non 360.R !
Sinon, je reprends le formulaire déjà justifié en arrondissant à trois chiffres significatifs ; attention : je conserve tout de même en mémoire de ma calculatrice tous les chiffres significatifs ; sinon, les arrondis successifs pourraient conduire à des erreurs... Ma calculatrice est réglée en mode "radians".
Remarque : une fois les calculs effectués, il faut rapidement tester leur "'réalisme"...
1° : Le centre de gravité G1 est évidemment à l'intérieur du secteur circulaire : OG est donc nécessairement une grandeur inférieure à R = 54cm et supérieure à .
2° : on remarque : OI>OG1 : la partie enlevée au secteur circulaire est décalée vers l'extérieur, ce qui décale vers l'intérieur le centre de gravité G de la partie restante. On obtient donc : OG<OG1
3° on remarque : : le petit disque qui est enlevé représente un peu moins du huitième de la surface du secteur circulaire donc un peu moins du huitième de sa masse ; de plus, les points G1 et I sont proches. Dans ces conditions, enlever ce petit disque ne déplace que de très peu le centre de gravité : OG n'est donc que de très peu inférieur à OG1 (écart relatif de 0,4%).
Annuler
connectez vous