Bonjour
C'est vrai qu'on ne trouve pas grand chose. Le point de Lagrange L1 étant instable on ne peut pas vraiment parler d'orbite et, si le satellite reste au voisinage de L1 c'est au prix de corrections régulières de trajectoires, sinon le satellite s'éloignerait définitivement de L1 pour aller graviter autour de la terre ou du soleil.
Voici ce que j'ai trouvé de plus précis :

Il y a quelques temps, j'ai créé une fiche d'aide sur le sujet, niveau (bac+1). Ton niveau est supérieur mais tu y trouveras peut-être quelques renseignements utiles... Il s'agit de la fiche n° 9 du site.

Merci beaucoup pour votre réponse
Je vais regarder ça tranquillement. En tout cas votre fiche n'9 a l'air très bien expliqué.
Que pensez vous si je prends une vitesse moyenne de 10metres par seconde ?

Le choix de cette vitesse est crucial si on veut que le satellite reste "assez longtemps" (trois mois dans ma simulation,  ce qui correspond sensiblement à la durée entre deux correction) au voisinage de L1. Personnellement, j'ai choisi 22,5m/s à l'apogée. Tu trouveras le résultat sur ma fiche. Une valeur un peu plus grande ou un peu plus petite fait s'éloigner le satellite très vite de L1. A noter que je me suis limité à un mouvement dans le plan de l'écliptique, ce qui n'est pas rigoureusement le cas dans la réalité.

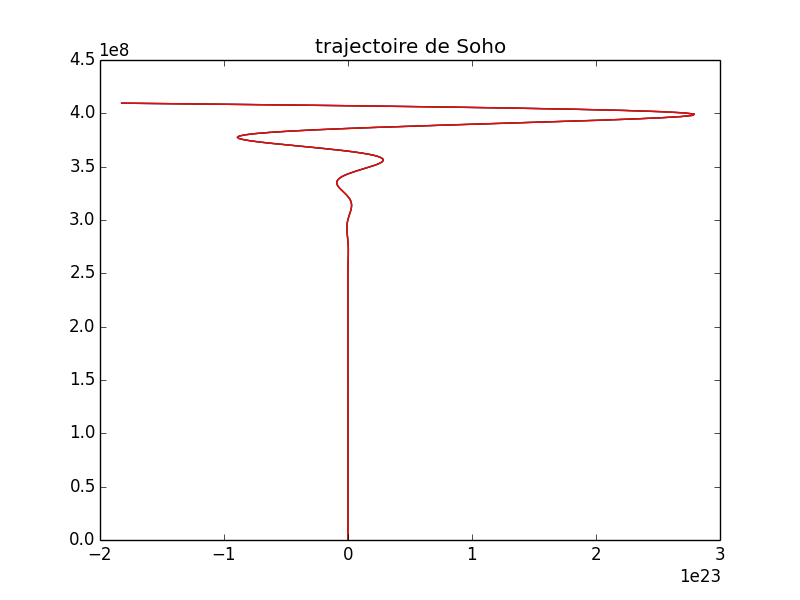
Bon, j'ai essayé de prendre des valeurs initiales en m'inspirant de vous deux liens mais le résultat semble très différent de ce que vous obtenez.
J'ai appliqué la méthode d'intégration d'Euler (sur Python) et j'ai pris comme valeurs initiales :
x0=1,4.10^14 mètres
y0=400000 kilométres
z0=600000 kilomètres
v0=20 m/s
Sachant que j'ai pris comme origine le barycentre des deux corps célestes, ici Terre et Soleil.
La trajectoire obtenue montre l'instabilité selon une certaine direction.
Qu'en pensez vous sinon ?

sachant que l'axe y et z (pour moi)sont inversés (pour moi) si je compare avec vos schémas

Bonsoir
Tu n'es pas assez précis pour que je puisse te répondre de façon précise...
Tu précises l'origine du repère mais pas les axes. Est-ce bien le repère tournant autour de l'axe Gz à raison d'un tour par année sidérale ? L'avantage de ce repère est que les points O,T et L1 sont fixes dans ce repère.
Tu ne précises pas non plus l'orientation de ton vecteur vitesse initiale. Je crois que tu aurais intérêt dans un premier temps à étudier le mouvement dans le plan de l'écliptique en choisissant Voz=0.
Le but de ce travail est de montrer que, si on choisit correctement les conditions initiales, le satellite reste quelque temps (quelques mois) au voisinage de L1 pour partir ensuite, si on ne corrige pas la trajectoire, graviter autour du soleil ou de la terre.
"Au voisinage" signifie : à des distance petites devant "a" avec a = OT = 1,5.10¹¹m (une unité astronomique).
Or, tu poses Xo>>a ! ton programme fait ensuite intervenir des distances allant jusqu'à 3.10²³m, largement en delà du système solaire !
Je crois que tu as tout intérêt à prendre l'origine de ton repère en L1.
Attention aussi à la méthode d'Euler (méthode basique ou méthode "améliorée" ?) ; il faut choisir un pas de calcul très faible : 50s par exemple, ce qui suppose un nombre de points de calcul très élevé.

Oui désolé je n'etais pas très précis.
Je me place bien dans le repère tournant ayant pour origine le barycentre des deux astres(voir schéma).
Vous aviez raison je me suis trompé dans la valeur de x0. Je cherchais à prendre une valeur proche de l'abscisse du point L1. Or en refaisant le calcul je trouve x0 environ égale à 1,48.10¹¹ m.
J'ai ensuite utilisé la méthode basique ... :/ avec un pas de 60 sec pour une durée d'étude de 3 mois.
Je vais essayer d'améliorer tout ca

Malheureusement je ne peux poster mon schéma en raison des dimensions trop importantes. C'est la même chose que dans votre fiche sauf que votre axe (Gy') correspont à mon axe z et inversement.

Je ne suis pas spécialiste du langage python. Je travaille plutôt sous MATLAB... Est-il possible de faire figurer en plus de la trajectoire du satellite, la position L1?
Je te rappelle que tu dois obtenir, sur une durée longue, un mouvement autour de la terre ou autour du soleil, selon les conditions initiales... Si, le satellite ne se dirige pas vers un de ces astres, il y a nécessairement erreur...

oui il est surement possible d'afficher le point L1.
Mais à vrai dire, ne pas trouver le résultat que vous décrivez me semble bizarre ... mes equations ont l'air bonnes pourtant ... Je vais essayer d'appliquer la méthode ameliorée d'Euler et de placer L1 comme origine de mon repère.  

Bonjour
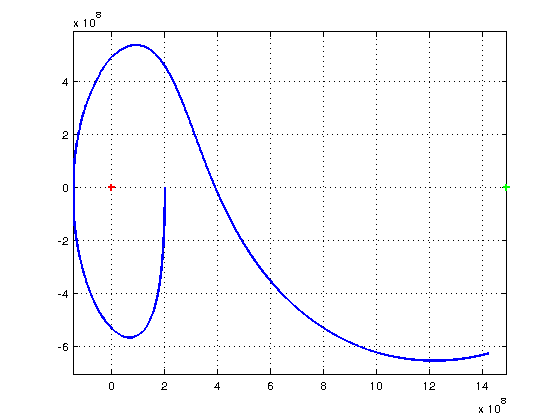
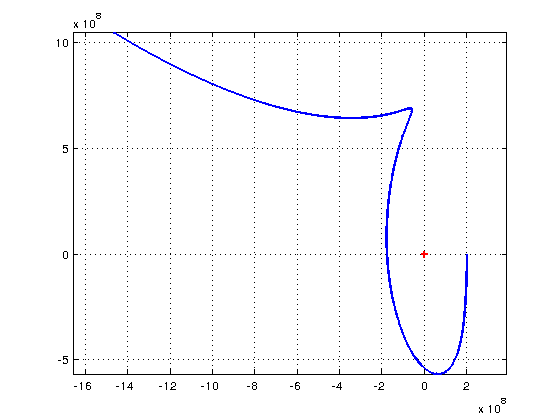
Pour illustrer le caractère "crucial" du choix de la vitesse initiale, voici deux exemples de simulation sur une durée de 6 mois. La position initiale est la même : Xo=2.10⁸m ; Yo=Zo=0 ;
Premier cas : Voy=-244m/s ; Vox=Voz=0. Le satellite décrit un peu plus de 3/4 de tour autour de L1 (croix rouge) pour finalement partir orbiter autour de la terre (centre de la terre matérialisé par la croix verte).
Deuxième cas : Voy=-245m/s ; Vox=Voz=0. Le satellite décrit un peu moins de 3/4 de tour autour de L1 (croix rouge) pour finalement partir orbiter autour du soleil...
Et l'écart de vitesse initiale n'est que de 0,4% !

Wow.. la différence est impréssionnante  ...
J'essaye (encore ...) de continuer mon programme de mon côté. Mais quoiqu'il en soit l'ordre de grandeur reste beaucoup trop important... et je ne vois pas d'où cela peut venir.
Je vais tout recommencer

Mon nouveau résultat se rapproche.
j'ai mis x0=0
y0=600000km
un pas de 60 sec pour une durée d'etude de 90 jours.
Le repère est centré en L1.
vx0=20
vy0=0
qu'en pensez vous ?

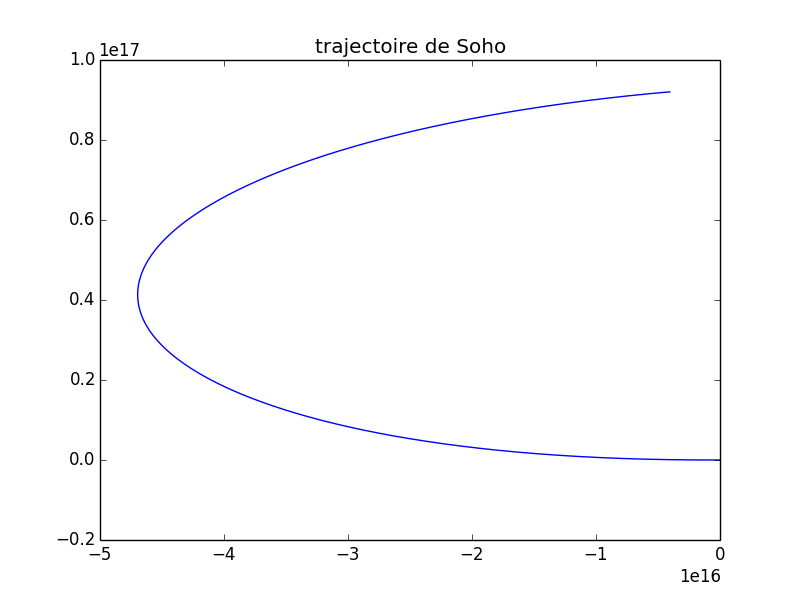
Les choses s'améliorent mais je crois que tu as toujours un problème d'ordre de grandeurs : les distances à L1 doivent, pendant "quelque temps", rester très inférieures à la distance terre- soleil qui vaut  a = 1,5.10^11m et même rester inférieure à la distance de L1 au centre de la terre égale à environ 1,5.10⁹m alors que tu obtiens très rapidement des distances de l'ordre de 500 000 fois la distance terre - soleil.
As-tu comparé tes équations différentielles à celles que j'utilise ?

Voici mes équations différentielles:
r0= distance soleil -barycentre
Rs=distance soleil-L1
Rt=distance L1-Terre

a_x= -G.M_sol.(x+Rs)/[(x+Rs)²+y²]^3/2 -G.M_T.(x-Rt)/[(x-Rt)²+y²]+(x-r0+Rs).²+2..vy

a_y= -G.M_sol.y/[(x+Rs)²+y²]^3/2 -G.M_T.y/[(x-Rt)²+y²]+y.²-2..vx

La seule différence vient dans l'expression de la force d'inertie d'entrainement selon x.

r0=450 km
Rs=1,48.10¹¹ m
Rt=1,5.10⁹ m

Bonjour
Tu as peut-être aussi un problème d'arrondi de calculs. La résultante des forces est extrêmement faible au voisinage de L1. Personnellement : lors d'un premier essai de tracé des équipotentielles au voisinage de L1, j'avais arrondi la distance  L1 T à trois chiffres significatifs : je me suis retrouvé avec un maximum d'énergie potentielle à plusieurs milliers de km de L1 ! Un conseil : entre dans ton logiciel les valeurs de GMs et GMt et a les plus précises actuellement connues que tu peux trouver ici :

Conserve tout au long de ton étude les valeurs calculées de ro, Rs et Rt et non pas les valeurs arrondies.
Pour ta simulation, tu utilises la méthode d'Euler simple ou la méthode améliorée ? La méthode "simple" diverge très vite...

D'accord je vais suivre vos conseils
J'utilise la méthode simple pour l'instant ... j'ai quelques problèmes avec la méthode améliorée
Je vais essayer de m'en occuper cette aprem

J'ai affiné chaque valeurs et j'ai réussi à faire le programme version améliorée ... Mais le résultat obtenu est analogue au dernier obtenu ... Je perds pas espoir, y a forcement un problème quelque part

Bonjour vanoise,
j'ai une autre question concernant votre fiche. Pour montrer l'instabilité du point L1, j'ai calculé les dérivées seconde d'energie potentielle, puis j'ai évalué leur signe ... bref une manière pas très belle. Votre approche est quand même un peu plus "classe". Cependant je ne comprends pas pourquoi vous arrivez à conclure que " Le point L1 correspond à un maximum d'énergie potentielle "

Je sais que F =−m·grad(e_p) donc F orthogonal aux équipotentielles et orientés dans le sens des énergies potentielles décroissantes. Mais après j'ai du mal à visualiser avec votre tracé.
Pouvez vous m'éclairer ?

Bonjour
Regarde bien le tracé des équipotentielles. Le niveau ep=0 a été choisi arbitrairement en L1. L1 est ce qu'on appelle un "col" d'énergie potentielle par analogie avec un col en montagne : le sommet du col est un maximum d'énergie potentielle de pesanteur pour le cycliste qui roule suivant une direction approximativement perpendiculaire à la ligne de crêtes. En revanche, le sommet du col est un minimum d'énergie potentiel pour un alpiniste qui se déplace le long de la ligne de crêtes. L1 est un maximum d'ep par rapport à x et un minimum d'ep par rapport à y et par rapport à z. Cela peut effectivement se démontrer en calculant les dérivées partielles de ep par rapport à x et y.
Pour qu'une position d'équilibre puisse être qualifiée de stable, il faut que les forces conservatives ramènent S vers cette position quelle que soit la direction dans laquelle  S a été écarté de cette position et abandonné sans vitesse initiale. Cela n'est pas le cas pour les points de Lagrange.

Ok merci beaucoup je comprends mieux maintenant