Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

Caractère conservatif

Posté par
pfff 22-03-21 à 18:18

Bonsoir j'aimerais un peu d'aide pour cet exercice. Merci

Mr X assimilé à un point M, soumis à la force \vec{F}, doit parcourir deux chemins (a) et (b) et déterminer si \vec{F} est conservative. M est repéré par ses coordonnées polaires r et \theta. Le chemin (a) est un arc de cercle de rayon R tandis que le chemin (b) est constitué de deux segments de droites AC ET CB de longueur R. Les deux chemins sont issues de A et mènent à B. La force \vec{F} s'écrit \vec{F} = r²d²\vec{u_\theta} en coordonnées polaires, où d est une constante.

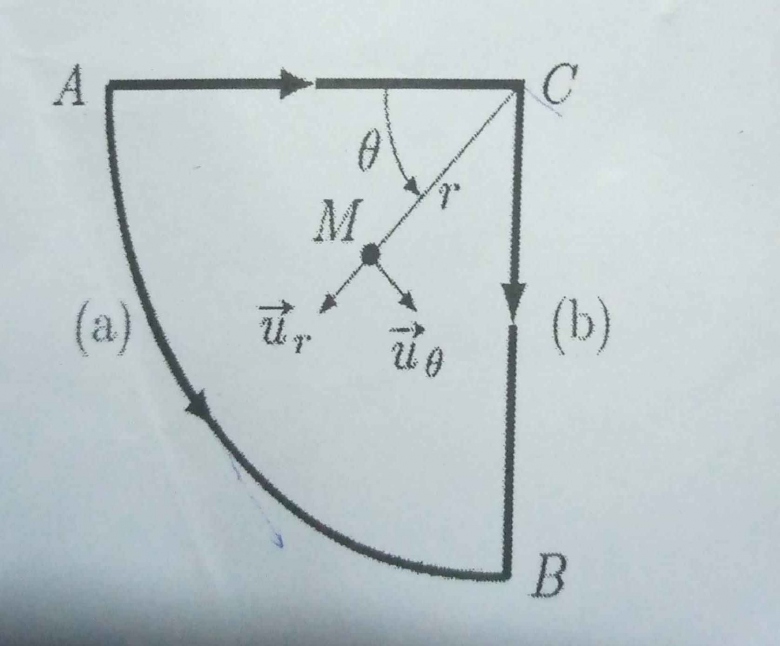
Caractère conservatif

1. Déterminer le travail W de la force \vec{F} pour les deux chemins envisagés. Conclure quant au caractère conservatif de \vec{F}.

2. Réitérer avec la force \vec{F'} = r²d²\vec{u_r}


3. Déterminer l'énergie potentielle dont dérive la force envisagée qui est conservative. On pourra par exemple utiliser un déplacement élémentaire sur le chemin CB.

J'ai longuement réfléchi mais je n'arrive pas à faire la question 1

Posté par
vanoisere : Caractère conservatif 22-03-21 à 19:16

Bonjour
Commence par établir les expressions de F suivant les trois chemins : l'arc de cercle et les deux chemins rectilignes.

Posté par
pfffre : Caractère conservatif 22-03-21 à 19:28

Pour F on a :

Caractère conservatif

Posté par
pfffre : Caractère conservatif 22-03-21 à 19:31

sur l'arc de cercle on a :
\vec{F} = r²d²\vec{u_\theta }


Sur les autres trajets je ne vois pas trop

Posté par
vanoisere : Caractère conservatif 22-03-21 à 20:05

OK pour l'arc de cercle avec une simplification : r=R=constante ; cela va te simplifier le calcul du travail !
Quand M appartient au segment (AC) : comment est orienté le vecteur \vec u_\theta ; la réponse à cette question permet d'obtenir le travail de A à C sans le moindre calcul. Même chose quand M appartient au segment (CB)...
De façon générale, l'expression générale du travail élémentaire de la force s'écrit :

\delta W=\overrightarrow{F}.\overrightarrow{dl}

Quelle est l'expression du travail lors du déplacement sur l'arc de cercle ?

Posté par
pfffre : Caractère conservatif 23-03-21 à 00:26

la distance élémentaire sur l'arc de cercle je ne vois pas trop comment la déterminer

Posté par
vanoisere : Caractère conservatif 23-03-21 à 10:36

Tu as sans doute étudié en cours l'expression générale du déplacement élémentaire \vec{dl} en coordonnées polaires...
Et pour les directions du vecteur \vec F sur les parcours rectilignes (AC) et (BC) ? Relis si nécessaire mon message de hier soir 20h05.

Posté par
pfffre : Caractère conservatif 23-03-21 à 11:18

Ah oui en coordonnées polaires on a :

\vec{dl} = dr\vec{u_r} + rd\theta \vec{u_\theta }

finalement sur l'arc de cercle on a :

W = \int \vec{F}.\vec{dl} = \int r²d²\vec{u_\theta }.rd\theta\vec{u_\theta }
W = W = r^3d²\theta

Posté par
pfffre : Caractère conservatif 23-03-21 à 11:21

je pense que sur les trajets AC ET BC \vec{u_\theta } est orienté perpendiculairement

Posté par
vanoisere : Caractère conservatif 23-03-21 à 11:36

Sur l'arc de cercle, puisque r=R = constante :

W_{AB}=\int_{0}^{\frac{\pi}{2}}R^{3}.d^{2}.d\theta=R^{3}.d^{2}.\int_{0}^{\frac{\pi}{2}}d\theta=R^{3}.d^{2}\cdot\frac{\pi}{2}
OK avec ton message de 11h21. Que peut-on en déduire des travaux de A à C et de C à B ?
Remarque : on peut aussi partir de l'expression générale du travail élémentaire et constater que, sur les trajets rectilignes AC et CB, l'angle  polaire reste fixe : d\theta=0

Posté par
pfffre : Caractère conservatif 23-03-21 à 11:58

On a donc un travail nul sur ces deux trajets

Posté par
pfffre : Caractère conservatif 23-03-21 à 12:08

donc F n'est pas conservatif

Posté par
pfffre : Caractère conservatif 23-03-21 à 12:14

2) pour F'

sur l'arc de cercle on a :

\vec{dl} = dr\vec{u_r} + rd\theta \vec{u_\theta }

W = \int_{0}^{\infty }{\vec{F'}.\vec{dl}} = \int_{0}^{\infty }{R²d²dr}

je vois pas comment calculer

Posté par
vanoisere : Caractère conservatif 23-03-21 à 12:30

"donc F n'est pas une force conservative. D'accord !
Pour F', ton expression du travail élémentaire, qu'il faudrait écrire pour une rédaction claire, semble correcte. Maintenant, il faut ajuster les bornes d'intégration selon les trois parcours étudiés. Que vaut dr lors du déplacement sur l'arc de cercle ? Là encore, tu pourrais réfléchir aux directions des vecteurs \vec F et \vec{dl}

Posté par
pfffre : Caractère conservatif 24-03-21 à 06:14

sur les chemins AB et BC on a dr = 0
mais sur l'arc de cercle je ne vois pas

Posté par
vanoisere : Caractère conservatif 24-03-21 à 07:52

C'est juste l'inverse... Réfléchis un peu à ce que sont les coordonnées polaires. Aide-toi de schémas si nécessaire pour chacune des trois situations.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !