Inscription / Connexion Nouveau Sujet
calculs d'isolation
Bonsoir qui pourrait corriger mes calculs d'isolation(je pense que au niveau du flux thermique et déperdition mes résultats sont trop élevé

Bonsoir
Tu calcules la résistance thermique équivalente en ajoutant les résistances : très bien.
Seulement ensuite, le flux thermique fait intervenir la conductance thermique équivalente qui est l'inverse de la résistance équivalente . Ce n'est pas ce que tu as fait en ajoutant les conductances thermiques .
Je n'ai pas tout à fait compris par rapport au flux thermique on est d' accord que pour calculer la calculer j ai fait l inverse de la résistance qui est (épaisseur/lambda) quelle est la différence entre la conductance thermique et la conductance thermique équivalente ?
J'ai parlé de conductance équivalente car ton mur est composé de deux matériaux différents. Parle simplement de conductance du mur si tu préfères. Tu as commis une grosse erreur d'ordre mathématique en écrivant que la somme des inverses est l'inverse de la somme. Je développe. Je préfère raisonner directement sur la résistance des murs en tenant compte de leur surface d'aire S. Raisonner sur les conductances par unité de surface est possible mais peut se révéler piégeant dans certains cas.
La résistance thermique Rth est donc la somme des résistances thermique des deux matériaux comme tu l'as écrit :
La conductance thermique est ainsi :
D'où le flux thermique :
Si je comprends bien ton calcul, tu as écris :
C'est une grosse erreur :
; comme déjà dit : l'inverse d'une somme n'est pas égale à la somme des inverses.
Donc si j ai bien compris l'inverse d'une somme n'est pas égale à la somme des inversés comme vous m'avez montré l exemple donc je dois opter pour qu'elle formule car la seule formule que on a vu en classe est (lambda/épaisseur) *deltaT pour trouver le flux thermique
La formule que tu évoques dans ton dernier message est valide dans le cas d'une conduction thermique à travers un seul conducteur. Cette formule est tout de même très "réductrice". Tu as tout de même entendu parler de résistance thermique et de conductance thermique. Quand un flux thermique traverse successivement plusieurs couches de matériaux, les résistances thermiques s'ajoutent, pas leurs inverses que sont les conductances thermiques.
Il y a une analogie à faire avec les résistances électriques mais pas sûr que cela soit à ton programme.
Ah d'accord je viens de comprendre tout cela s explique l exemple qu on a vu en cours n'a que une conduction thermique donc dans le cas où il y en a plusieurs la formule c est quoi? Non je ne crois pas que sa soit dans le programme jamais entendu parler de résistance électrique
Dans le cas de plusieurs couches de matériaux différents, tu utilises la méthode que je t'ai fournie dans mon message de 12h54.
Nos deux messages précédents se sont croisés...
Je te laisse la responsabilité des valeurs numériques. Selon ma calculatrice :
Attention : une application numérique sans unité (lorsque celle-ci existe) ou avec une unité fausse, est considérée comme fausse le jour d'un concours ou d'un examen.
Non ! Le flux thermique correspond à une puissance thermique qui se mesure en watts.
La densité de flux thermique , souvent noté j ou jth ou jQ, se mesure en W/m2
Je t'avais déjà mis en garde sur les dangers d'un raisonnement toujours rapporté à l'unité de surface.
Ah oui effectivement et aussi J'aurai une dernière question après avoir calculé le flux thermique je veux calculer la déperdition du mur et elle est égale à flux thermique *surface et l unité et en Watt C est bien sa?
Tu n'as vraiment pas compris le rôle de la surface dans ce genre de problème.
Φ désigne le flux thermique qui traverse le mur donc la puissance thermique perdue par conduction à travers le mur , ce que tu peux appeler déperdition thermique. Φ dépend déjà de S...
La déperdition thermique à travers les murs est ici de 191W

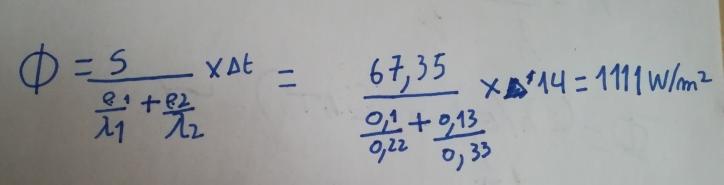
 1=0,022 et non 0,22 W.m-1.K-1
1=0,022 et non 0,22 W.m-1.K-1
