Inscription / Connexion Nouveau Sujet
Calculer la valeur maximal de l'angle d'incidence
bonjour,
je suis bloqué sur un exercice d'optique et j'aimerais bien avoir un peu d'aide. Je pense que je ne vois pas ce qu'il faut voir d'où
mes difficultés à m'en sortir ..
Je m'explique, voici l'énoncé pour commencer :
Un rayon lumineux se propageant dans l'air arrive à la surface d'un cube transparent dont l'indice de réfraction est 1.38.
Calculez la valeur maximale de l'angle d'incidence pour laquelle il y aura la réflexion totale sur le côté adjacent (point A).
J'ai essayé de faire la figure du mieux que je peux 
l'angle 0a s'appelle en réalité 
a
voila voila merci d'avance à ceux qui vont m'aider 
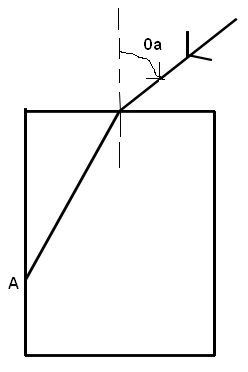
L'angle d'incidence limite pour lequel le rayon frappant la face verticale au point A subit une réflexion totale correspond à un rayon émergent du point A contenu dans le plan de la face verticale.
Salut Priam,
j'ai fais un petit dessin sur une feuille pour m'aider à mieux comprendre la situation.
est-ce que c'est bien comme ça que ça doit se passer?
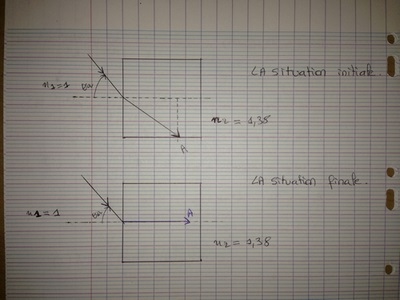
Je pense que le dessin que je t'ai montré correspond à la réfraction limite non?
donc le bon dessin serait (avec la réflexion totale) le suivant? (la situation finale n°2)
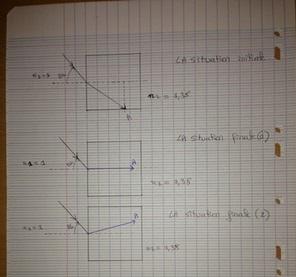
j'ai enfin réussi!
sin i2 = n1/n2 x sin i1
donc sin i2 = n1/n2
donc sin i2 = 1/1.38
donc i2 = sin-1(0.72)
donc i2 = 46.4°
connaissant l'angle 46.4°, j'utilise la propriété qui dit que dans un triangle rectangle,
la somme totale des angles fait 180°. (on sait qu'on est ici dans un triangle rectangle car
on sait que la normale est perpendiculaire du dioptre).
donc 180 - (90+46.4)= 43.6
on trouve directement l'autre angle qui donne 43.6°
maintenant pour trouver l'angle maximale a on utilise la formule de Descartes
n1sini1 = n2sini2
donc ici n1 sin a = n2 sin i2
sin a = 0.95
a = sin-1(0.95)
donc a = 71.8°
Hop, exercice terminé!
Annuler
connectez vous