Inscription / Connexion Nouveau Sujet
Calcul U
Bonjour,
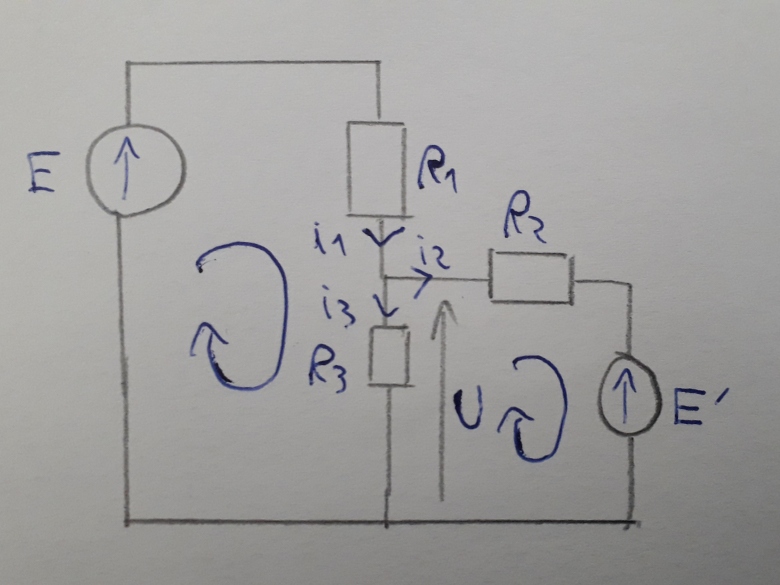
Déterminer la tension U en fonction des valeurs des résitsances et des générateurs.
Loi des mailles dans la maille de gauche: E-R1.i1-R3.i3=0
Loi des mailles dans la maile de droite: E'-R3.i3-R2.i2=0
Ici je suis pas sûr des signes car la flèche du générateur E' indique vers le haut et le sens du courant est vers le bas.
Loi des noeuds: i1=i2+i3
Je résous le système a 3 équations et 3 inconnus pour trouver i3.
U=R3.i3
J'ai la bonne démarche ? Existe t-il une manière plus simple ?
Merci d'avance
U = [(E/R1)+(E/R3)+(E'/R2)] / [(1/R1)+(1/R2)+(1/R3)] ?
Et si je veux appliquer la loi des mailles sur la maille de droite,je souhaite respecter les conventions générateurs et récepteurs alors je parcours la maille du sens trigonométrique: E'-(-i2.R2)-i3.R3=0 , c'est bien ça ?
La loi des mailles, ou plus simplement, la loi d'addition des tensions, conduit ici à :
Tu peux faire confiance à ma longue expérience de correcteur de concours de niveaux bac+2 et plus : la loi des mailles doit être connue mais il s'agit rarement de la meilleure méthode dès que le circuit se complique un peu. Outre les problèmes de signes souvent rencontrés, elle génère un nombre important d'inconnues que les étudiants peinent ensuite à éliminer. Souvent, les étudiants « tournent en rond » pour arriver, après un long calcul à (par exemple) : i1=i2+i3 . Beaucoup de temps perdu un jour d'examen ou de concours !
Si tu ne maîtrises pas bien le théorème de Millman, tu peux partir de la loi des nœuds pour remplacer aussitôt chaque intensité par son expression déduite de la loi d' Ohm, sans passer par la loi des mailles. Cela donne ici :
Il suffit alors d'isoler U et on obtient l'expression qu'il aurait été possible d'obtenir directement par le théorème de Millman :
Si cela t'intéresse : plus de renseignements sur le théorème de Millman ici :
![]()


