Bonjour, pourrait-on avoir un schéma stp

Désolé, mais je ne suis pas vraiment doué en info.

Je récapitule :
Effort : 15000 N
Barre verticale encastrée de longueur 1.6m
Barre à 45° encastrée de longueur 1.8m

D'où ma question, comment procéde-t-on pour résoudre ce système hyperstatique et connaitre la réaction en A, le moment d'encastrement en A, la réaction en B et le moment d'encatrement en B ?

Je ne connais pas la définition d'un moment d'encastrement mais je peux dire comment je vois la répartition des forces sur le système.

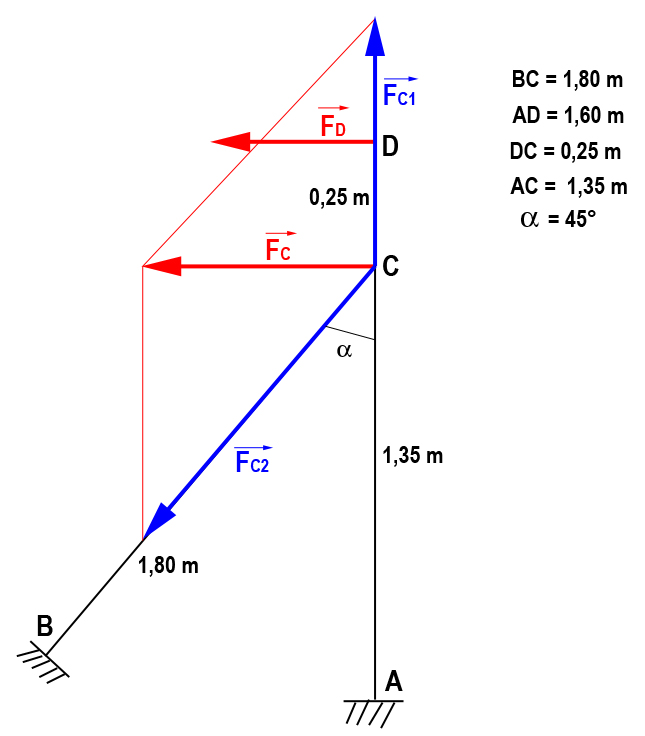
Ce n'est qu'un détail mais les points A et B ne peuvent pas être au même niveau (si l'angle fait 45°)...
La force (15000 N) est appliquée sur l'extrémité de la poutre AD. Elle crée une force    au point C.
On peut calculer les moments de ces forces




Plus est petit, plus F_C2 est grande...

Il est nécessaire de considérer plutôt la force F_C perpendiculaire à la poutre AD afin de la décomposer sur les deux directions AD et BC. On a alors :


On décompose en deux vecteurs selon AD et BC :   et  




  est dirigée vers le haut. Je l'aurais vu, a priori, dans l'autre sens mais c'est le résultat de l'addition des vecteurs... On ne peut rien contre ça...

Quant au moment d'encastrement...
Ces résultats sont sous toutes réserves car je ne suis nullement spécialiste de ce domaine...

Tout d'abord, j'ai fait une erreur dans l'énoncé : il ne faut pas tenir compte du 250mm. Tu l'avais bien vu et merci de ton aide.

Je travaille en BE mécanique et ceci est un cas concret. Mes cours de résistance des matériaux sont bien loin et je ne sais plus comment on fait pour résoudre ce système hyperstatique, mais je sais qu'il y a au moins une méthode.

Si je ne m'abuse, tu as utilisé une méthode plus mathématique avec des scalaires, mais les résultats semblent logiques : l'appui en A ( qui est une platine ancrée au sol avec des chevilles ) est soumis à la traction ( arrachement ).
L'appui en B ( qui est aussi une platine ancrée au sol dans le même plan que A ) est soumise à Fc2 qui se décompose en une force F'c2 horizontale ( qui provoque le cisaillement des chevilles ) et en une force F''c2 verticale vers le bas ( qui provoque la compression de la platine ).

En résistance des matériaux, on utilise un peu la même méthode en appliquant le principe fondamental de la statique ( PFS ) : si un système est à l'équilibre, alors :
* la somme des forces extérieures qui lui sont appliquées est nulle
* la somme des moments des forces extérieures est nulle.
Pour tenter d'expliquer le moment d'encastrement, il faut savoir qu'en RdM les poutres qu'on étudie ont à 3 grands types d'appuis possibles :
* appui simple qui provoque une réaction normale ( une seule inconnue )
* appui rotule qui provoque une réaction à 2 composantes ( 2 inconnues )
* encastrement qui provoque une réaction et un moment dit d'encastrement ( 3 ou 4 inconnues )
Donc, si on applique ici le PFS, on va se retrouver avec plus d'inconnues que d'équations ( système hyperstatique ).

Ouf, désolé pour la longueur de l'explication, y a t il un mécano dans le coin qui connaisse l'astuce pour trouver l'équation manquante par la méthode classique de RdM !

D'après ce que j'ai fait, il y a effectivement une compression sur la jambe de force donc en B et un arrachement en A...
Maintenant, je n'ai fait que de la physique, pas de résistance des matériaux. Ce que j'ai utilisé, c'est purement des forces et des moments de force, comme on apprend en physique...
Le moment d'encastrement, je ne connais pas donc je ne peux pas faire mieux...
Y a-t-il un "mécano" sur ce forum ?... Je ne sais pas...

Merci beaucoup de ton aide, ça me permet au moins de connaitre les efforts dans chacune des 2 barres.

Ce n'est pas si simple.

Dans un système hyperstatique, il n'y  a pas de solutions mathématiques simples.

Les barres étant rigides (pas des cordes), on n'a pas du tout le droit de supposer que l' effort dans une barre a la même direction que la barre car la barre peut être soumise à de la flexion (ou a de de torsion dans certains cas).

On peut décomposer chaque effort (en A, en B et en C) en sa composante verticale et sa composante verticale.
On a donc 6 inconnues qu'on peut noter FAx, FAy, FBx, FBy, FCx, FCy

On peut facilement écrire 5 équations reliant ces 6 inconnues en exprimant que :

1) La somme des composantes verticales de toutes les forces sur la barre = 0
2) La somme des composantes horizontales de toutes les forces sur la barre = 0
3) Le moment des forces autour du point A = 0
4) Le moment des forces autour du point B = 0
5) Le moment des forces autour du point C = 0

On a donc un système de 5 équations à 6 inconnues qu'on ne peut pas résoudre.

... Sauf si on rend le système non hyperstatique, par exemple en remplaçant un encastrement ou une jonction de barre par exemple une rotule ou ... pour imposer une direction de force.

Sauf distraction.  

Ah bon ( déception ... )
lol

Il me semblait bien que l'astuce consistait à remplacer le système par 2 systèmes isostatiques, ou un truc dans le genre ...
Mon chef va pas être content si le support ou les fixations cassent à la première utilisation !
je vais lui dire que c'est pas pôssible.
Ouf je suis sauvé !!

Merci

Le fait qu'on ne peut pas calculer n'implique pas que cela va casser.

oui, bien sûr. Je plaisantais.

Je viens de retrouver mes cours sur le sujet et il y a bien une méthode appelée méthode des forces.
Cela consiste à déterminer pour le système hyperstatique à résoudre, un système équivalent composé :
* d'un système iostatique dit système isostatique associé
* de conditions cinématiques ( c'est à dire portant sur les déplacement et les déformations ), pour le système isostatique associé.

Je vais essayer de me dépatouiller avec ça, si j'y arrive je posterai la réponse, si ça intéresse quelqu'un ( autre que mon chef )...

D'autre part, je m'interroge si j'ai bien fait de  modéliser mes appuis en encastrement ?? ( ce sont des profilés acier en H ( HEB ) soudés sur des toles épaisses ( 15mm) )
Qu'en pensez-vous ?

Bonjour

J'ai le même problème que vous a résoudre.
Sauf qu'au lieu de 15000 j'ai 2700 DAN en force axial vers A.

Pouvez vous m'aider en postant votre réponse?

D'avance merci.