Inscription / Connexion Nouveau Sujet
Calcul résistance conducteur ohmique cylindrique homogène
Bonjour,
Voilà j'ai un schéma pour bien voir ce dont on parle :
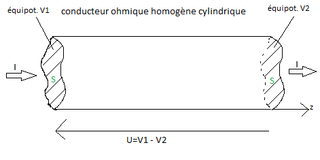
Le cylindre est de longueur L (de z=0 à z=L)
Voilà pour calculer R à l'aide de la loi d'Ohm U=RI j'ai besoin de calculer le potentiel V en fonction de z
Le problème c'est que j'ai un démo ou il est écrit :
en z=0, V=V1
en z=L/2, V=V2
ça je suis d'accord
Mais après je ne comprend pas pourquoi en z=L/2 V=V1 +(V2-V1)/2
Quelqu'un peut de débloquer ?
Merci
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]()
Bonjour,
En utilisant la loi d'Ohm locale et le fait que
(flux de J conservatif, ici S_1 = S_2 puisque la section est constante) vous devriez pouvoir remonter au champ électrique et donc au potentiel.
c'est quoi cette formule je comprend pas, je connais i(t)=



Mais en fait dans la démo que j'ai il est claqué direct que pour z=L/2, V = V1 +(V2-V1)/2
Y-a-t-il quelque chose d'évident pour pouvoir dire cela qui m'échapperait ?
up je ne comprend toujours pas
pourquoi peut-t-dire directement sans aucun calcul que V(z=L/2)=V1+(V2-V1)/2
Bonjour,
Ma formule est la même que la votre avec des notations différentes.
Ce qui est évident c'est donc
puisque
. Et donc
avec de plus ici
en raison de la géométrie. Et comme E = cte, oui, c'est évident.... non ?
remarque : je ne fais pas de rédaction détaillée, mais il faut justifier que les lignes de champ qui sont également les lignes de courant sont paralèlles à l'axe du cylindre. Ce qui est... évident là aussi. Considérations de géométrie + propriétés des lignes de courant.
Ce qui est évident c'est
Vous basez votre démo la dessus mais pour moi ce n'est pas évident justement. Comment peut on dire justifier que j est constant ?
Re,
Il faut lire le message qui suit celui qui contient cette équation....
On se place dans le cas où la longueur du fil est beaucoup plus grande que son rayon. On peut alors faire l'approximation d'un fil infini.
On a également une symétrie par rotation continue autour de l'axe de ce fil. On a donc .
On sait qu'en régime permanent , soit ici
. Donc
est constant. Par suite le vecteur correspondant l'est également.
Est-ce que cela est plus clair pour vous maintenant ?
Les arguments sont classiques et cela sert dans un tas de situations : les symétries permettent de dire que ne dépend que d'une seule coordonnée et le régime stationnaire entraîne sa constance.
Re,
Désolé, j'ai écris des connéries.....
On appelle l'axe du fil. Dans une section du fil, on prend les coordonnées polaires
.
Alors :
- symétrie continue par translation selon l'axe =>
- symétrie continue par rotation autour de l'axe =>
Ensuite, le régime stationnaire entraîne toujours mais on ne peut plus dire grand chose, sauf que
.
Par contre, on peut toujorus intégrer sur une ligne de courant à pour trouver la tension (avec le loi d'Ohm locale, cf posts précédents) et on retrouve la dépendance linéaire du potentiel avec
.
Relisez, en particulier le passage : "Désolé, j'ai écris des connéries.....".
Et puis soyez un peu plus bavard, j'ai vraiment l'impression que soit :
- vous ne lisez pas ce que j'écrit
- vous ne comprenez pas ce que j'écris
- une combinaison linéaire des deux précédents....
J est constant sur toute la longueur du conducteur à distance fixe du centre. Donc, sur une ligne de courant est donc constant.
Question : savez-vous ce qu'est une ligne de courant ?
Ensuite, on a , donc si E dépend de
on aura des mouvements de charge radiaux, ce qui n'est pas le cas dans un conducteur cylindrique tel qu'utliisé ici, donc E est uniforme. Par conséquent J aussi.
Comme , une ligne de courant est aussi une ligne de champ. On peut donc calculer la différence de potentiel entre deux points A et B appartenants à deux sections droites équipotentielles distants de L :
.
Puis .
On a donc .
Si vous ne comprenez toujours pas, continuez à poster votre question sur tous les forums francophones comme vous avez commencé à le faire.... ![]()
Votre problème est essentiellement que vous ne comprenez pas la physique de la situation, les symétries, ce que les lois de bases impliquent.... mais c'est surtout le sens physique et la compréhension de la physique qui vous bloque. Un conseil : oubliez les équations un moment et réfléchissez à ce qui peut bien se passer dans ce foutu conducteur quand on fait circuler un courant dedans.... Comment bougent les charges, est-ce qu'elles pourrait bouger autreement ? Si oui, qu'est-ce que cela implique sur le champ électrique et le vecteur densité de courant volumique ?, etc, etc...
(Et puis, je suis monté à plus de 313,15 K.... alors je suis un peu K.O.)
@+
Pour moi une ligne de courant est en tout point tangente à j donc à E avec la loi d'Ohm
Je comprend bien qu'il faut montrer que E est uniforme dans le conducteur pour avoir l'uniformité de j,je comprend très bien les calculs de U et I.
Mais même avec votre explication j'ai toujours du mal à comprendre pourquoi E est uniforme. D'accord j'imagine bien que les charges se déplacent dans le sens du fil mais une intuition ne peut pas me servir de justification. Là où j'aurais besoin de plus d'explications c'est sur votre raisonnement :
si E dépend de
Comment justifier ça rigoureusement ?
Pour ce qui est des propriétés de symétrie à part en se plaçant sur l'axe du conducteur, il n'y a pas de symétrie ou d'antisymétrie de la distribution de courant.
Désolé j'abandonne, c'est au dessus de mes forces.
Vous ne comprenez ni ne maîtrisez les bases les plus élémentaires. Et j'ai expliqué la même chose en long en large et en travers, et vous ne faites toujours pas le moindre effort ne serait-ce que pour montrer que vous essayez de comprendre. Si vous êtes vraiment en math spé, je me demande bien comment vous avez pu y entrer.... et même si vous êtes en sup (comme indiqué sur l'autre forum).
J'hésite entre vous conseiller d'apprendre votre cours ou de vous réorienter vers une autre filière, loin, très loin, très très loin des sciences.
Bon courage pour la suite.
Ok sympa depuis le début j'essaie de comprendre tout ce que vous écrivez. Si je suis venu ici c'est bien pour ça non ?
Pourquoi ferais-je exprès de ne pas comprendre ? C'est assez tordu comme idée.
Je connais mon cours mais je ne comprend pas l'explication que vous donnez ça s'arrête là.
Est-ce que quelqu'un d'autre peut donner son point de vue sur le problème du potentiel qui varie linéairement selon z ?
Peut-être ça me débloquerait. J'aimerais bien parce ce que c'est vraiment le seul passage de mon cours que je ne comprend pas et ça doit vraiment être un truc tout con.


