Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Calcul Norme Champ électrique

Posté par
Lelaitcbon 10-09-20 à 18:25

Bonjour je bloque sur un exercice
pouvez vous m'aider svp ?

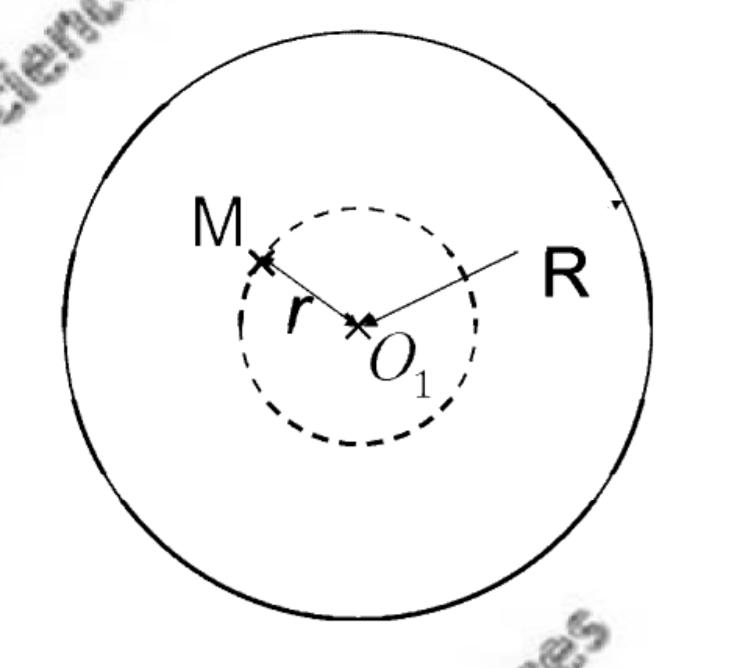
Une sphère de  centre O1 et de rayon R chargé uniformément en volume contient une charge totale Q>0 . On note p>0 sa densité volumique de charge

1)On me demande La norme du champ électrique E (en norme double barre) en un point M situé a l'intérieur de la sphère distant de r<R du centre

j'ai d'abord dit que E=\int \frac{KdQ}{(R-r)^{2}}ur=\int \frac{KpdV}{(R-r)^{2}}ur

mais apres je suis bloqué et j'hésite entre remplacer dV par 4pir^2 ou par la formule complete du volume sphere = 4/3pir^3

puis même si j'ai fait ca, je ne sais pas quoi faire avec  l'intégral puisqu'il ny a plus de dV etc

et je ne sais pas comment trouver une norme a partir d'une integrale

2- En choisissant le potentiel nul en O1, a propos du potentiel en un point M situé à l'intérieur  de la sphère distant de r<R du centre  et noté Vsphère(r) :
le potentiel Vsphère(r) est forcément négatif ou positif ?

donc ce que j'ai fais :

on me dit que le potentiel est nul en O1 donc il y a une cosntante non nulle
V(O)=\int \frac{KdQ}{(R)^{2}}+cste=0

donc cste = -\int \frac{KdQ}{(R)^{2}}


puis donc Vsphère(r)= \int \frac{KdQ}{(R-r)^{2}} -\int \frac{KdQ}{(R)^{2}}

Vsphère(r)=K \int dQ (\frac{1}{R-r}-\frac{1}{R})=K \int dQ (\frac{r}{(R-r)R})

K>0 Q>0 donc integraledQ >0 r>0   r<R donc R-r>0 donc V est forcement positif

et on  me dit qu'il est forcément négatif donc je ne sais pas pourquoi

pouvez vous m'expliquer


Merci

Calcul Norme Champ électrique

Posté par
gts2re : Calcul Norme Champ électrique 10-09-20 à 18:54

Bonjour,

Vous êtes parti dans une mauvaise direction : vous voulez intégrer des champs élémentaires, ce qui dans le cas sphérique est pour le moins compliqué : la distance au carré du dénominateur est la distance entre la charge élémentaire et le point M, donc "assez loin" de (R-r)  et je ne vois pas (sauf à admettre Gauss, voir plus loin) comment justifier le découpage en coquilles sphériques.

Pour ce qui est de dV=4r2, relire les réponses de vanoise au message "Electrostatique volume d'une sphère"

On a ici une symétrie sphérique, donc très forte, et dans ce cas on peut utiliser le théorème de Gauss.

Pour ce qui est du potentiel, si vous connaissez le champ, il n'est pas nécessaire de recommerncer un calcul d'intégrale, il faut plutôt utiliser la définition du potentiel.  

Posté par
Lelaitcbonre : Calcul Norme Champ électrique 10-09-20 à 19:13

Bonjour merci

mais quand vous dites que la distance au carré est assez loin de R-r, vous voulez dire quoi ?  je pensais que la distance a prendre en compte etait l'espace entre le cercle et M ce qui me donnait R-r ? est ce faux ?

ensuite, si j'ai bien compris ce que vanoise m'a dit, on me dit que la sphère est uniformément chargé donc rho p est la même partout j'aurai donc p=Q/V ? et donc V=4/3pir^3 .
Mais le probleme c'est que au départ j'ai dQ et non Q donc je dois remplacer dQ par pdV, et si j'enleve les d des dQ dV, l'integrale devient incensée non ? car elle n'est plus par rapport a telle variable ??

enfin pour la definition du potentiel, j'aurais tendance à dire que E=-gradV en vecteur, je determinerais le signe de V a partir de cette relation ?

a vrai dire je suis completement perdu, mes integrales sont surement fausses

Posté par
gts2re : Calcul Norme Champ électrique 10-09-20 à 19:49

Bonjour,

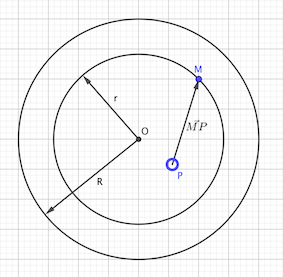
Si vous voulez calculer le champ en M par intégration, il faut écrire \vec{E}=\iiint k\frac{dQ \vec{MP}}{MP^3}, dQ étant la charge de l'élément de volume autour de P, l'intégrale étant prise pour P parcourant toute la sphère (on somme les champs créés par des charges ponctuelles). Donc très loin de ce que vous proposez qui est peu compréhensible : où avez-vous vu une telle expression ?

Par le théorème de Gauss, vous aurez juste besoin de calculer Q qui vaut en effet, si est constant, Q=V. Donc pas d'intégrale à calculer avec dQ.

Pour ce qui est du potentiel, c'est bien de cette relation qu'il faut partir.

Calcul Norme Champ électrique

Posté par
Lelaitcbonre : Calcul Norme Champ électrique 10-09-20 à 20:10

Merci pour votre réponse,
par contre je n'ai jamais étudié de triple intégration
je ne comprends pas votre schéma, n'est ce pas la sphère de rayon R qui est chargée et non la sphère de rayon r ?

ensuite,les formules dont j'ai utilisées viennent de mon cours
dE=\frac{Kdq}{r^{2}}ur
donc en sommant toutes ces petites charges, on integre E=\int \frac{Kdq}{d^{2}}ur

j'ai utilisée cette formule en sachant que la distance entre la charge et le point d'interet (M) soit distance d= R-r, ur le vecteur radial, ce qui me donne E=\int \frac{Kdq}{(R-r)^{2}}
p etant constant, j'ai donc Q=pV
donc
E= \frac{KpV}{(R-r)^{2}}ur (je pense que l'intégration se supprime du fait qu'il ny ait plus de dq ou dv)

ce qui me donnent a la fin E=\frac{pr^{3}}{3\varepsilon o(R-r)^{2}}

et je pense que pour le mettre en norme, je dois le le mettre au carré puis a la racine et donc le mettre sous valeur absolue ?

ma demarche ne marche pas ?

Posté par
Lelaitcbonre : Calcul Norme Champ électrique 10-09-20 à 20:11

oups j'ai oublié quelques vecteurs ur dans mes relations de mon message precedant

Posté par
gts2re : Calcul Norme Champ électrique 10-09-20 à 20:31

\vec{E}=k \frac{Q}{r^2}\vec{u_r} est vrai pour une charge ponctuelle et r est la distance entre la charge ponctuelle et le point d'observation.

Essayer de faire un dessin pour représenter :

Citation :
la distance entre la charge et le point d'interêt (M) soit distance d= R-r

vous verrez que votre d n'a pas grand sens puisque la charge est répartie dans la boule et que, comme il y a une intégrale, cela signifie que la charge élémentaire doit se déplacer dans tout le volume, donc que d varie ; or ici d=R-r est constant.  

\vec{E}=k \frac{Q}{r^2}\vec{u_r} marche aussi pour une charge à symétrie sphérique d'après le théorème de Gauss et dans ce cas r est la distance entre M et le centre de la sphère. Mais quitte à utiliser Gauss, autant l'utiliser complètement.

Citation :
par contre je n'ai jamais étudié de triple intégration

C'est bien pour cela que Gauss va être utile.

Posté par
Lelaitcbonre : Calcul Norme Champ électrique 10-09-20 à 20:44

Oh d'accord je comprends beaucoup mieux
mais si j'utilise le theoreme de gauss dans le cas d'une sphère j'aurais :
Eint.4\pi r^{2}=\frac{Qint}{\varepsilon o}
Eint.=\frac{Qint}{\varepsilon o4\pi r^{2}}
Eint.=\frac{\rho V}{\varepsilon o4\pi r^{2}}
E=\frac{\rho r}{3\varepsilon o}
est ce correct ?
et puisque je ne vois pas de vecteur , cette relation est deja une norme je suppose ?

mais comment savoir quand utiliser le theoreme de gauss a la place de faire les calculs de bases avec les intégrales ?

Posté par
gts2re : Calcul Norme Champ électrique 10-09-20 à 20:47

Citation :
je ne comprends pas votre schéma, n'est ce pas la sphère de rayon R qui est chargée et non la sphère de rayon r ?


La sphère de rayon R est chargée en volume, il faut donc intégrer sur toute la boule de rayon R : le point P parcourt donc tout la sphère, j'ai placé P à l'intérieur de la boule de rayon r parce que j'ai pensé à Gauss qui me parle des charges intérieures , mais le point P parcourt bien tout le boule de rayon R.

Posté par
Lelaitcbonre : Calcul Norme Champ électrique 10-09-20 à 20:50

gts2 @ 10-09-2020 à 20:47



La sphère de rayon R est chargée en volume, il faut donc intégrer sur toute la boule de rayon R : le point P parcourt donc tout la sphère, j'ai placé P à l'intérieur de la boule de rayon r parce que j'ai pensé à Gauss qui me parle des charges intérieures , mais le point P parcourt bien tout le boule de rayon R.


ah daccord je comprends mieux

Posté par
gts2re : Calcul Norme Champ électrique 10-09-20 à 20:53

Le théorème de Gauss fait intervenir \iint \vec{E} d \vec{S}, donc il y a projection du champ électrique sur la normale à la surface. Dans le cas présent, on obtient la composante radiale.

On utilise le théorème de Gauss dès qu'il y a suffisamment de symétrie  pour transformer
\iint \vec{E} d \vec{S} en \iint E d S et même finalment en E.S

Posté par
Lelaitcbonre : Calcul Norme Champ électrique 10-09-20 à 21:02

dans le cas d'une sphère il ya suffisamment de symetrie je suppose pour que j'utilise cette relation n'est ce pas ?
et donc ma relation est bonne ?

Posté par
gts2re : Calcul Norme Champ électrique 10-09-20 à 21:48

Oui on peut utiliser le théorème de Gauss et la relation obtenue est la bonne.

Il ne reste plus qu'à calculer V.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !