Inscription / Connexion Nouveau Sujet
Calcul du champ électrostatique créé par un ruban ?
Bonjour bonjour !
Je bloque sur un exo depuis plusieurs jours... La prof a dit qu'elle ne le corrigerait parce que c'était simple, mais je ne vois pas comment faire ! :s
Il s'agit d'un ruban chargé avec une densité uniforme 
.
Le ruban est dans le plan xOy, il a une largeur 2a (selon Oy) et une longueur infinie (selon Ox). Il est centré à l'origine, et le but est de calculer le champ en tout point M de l'axe Oz. M(0,0,z).
La prof nous a dit qu'il suffisait de "sommer" des fils de largeur négligeable pour obtenir le ruban. Sauf que je ne vois pas comment faire... Je veux bien calculer le champ créé par un fil au point M (et encore, c'est pas la joie, puisque le champ possède, sauf erreur de ma part, deux composantes, selon y et selon z), et après ?
Je suis dans le flou total, alors si pouviez m'éclairer sur la méthode à suivre... ! 
Merci d'avance !
bonjour,
la 1ere étape est de déterminer le champ d'un fil de longueur 2a et de densité linéique de charge 
en un point M du plan médian (cf figure)
est-ce que tu connais ce champ? sinon il faut le calculer.
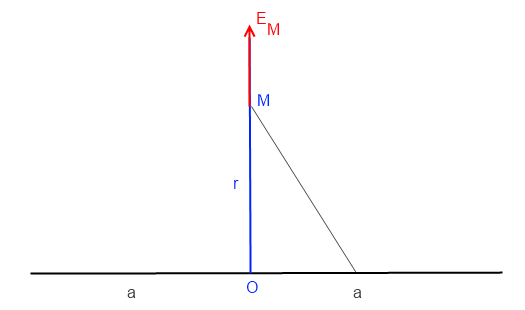
en fait le plus simple est de prendre le champ en M d'un fil infini!
puis de considérer le ruban comme la juxtaposition de fils de longueur infinie (selon Ox) et de largeur infinitésimale dy
Bonjour
La formule du champ créé par un fil infini est donné par
Si cette formule te pose problème nous la démontrerons plus tard.
En supposant que M est dans le plan x0z, le champ élementaire créé par un fil élémentaire est
Du fait de la symétrie, on a biensûr
Et par ailleurs:
A intégrer entre et
/r = z
@krinn
Ta première idée n'est pas la plus simple uniquement si tu considères la formule du fil infini comme acquise 
sinon l'intégration double est nécessaire et commencer par la largeur ne complexifie pas le problème ...
il me semble.
Annuler
connectez vous