Niveau master

Calcul densité d'états de phonons en 2D

Posté par
jybb 29-09-24 à 15:25

Bonjour,

Je cherche à calculer la densité d'états des phonons en 2D dans l'approximation de Debye ( $\omega = v k$ )

-- En 1D

Tous les $2\pi/L$ , on a un état (un vecteur d'onde k), et donc la densité "locale" pour un seul état est :

$g(k) = \dfrac{L}{2\pi}$

Ensuite on pose $g(k)dk = g(\omega)d\omega$ et donc $g(\omega) = g(k)\dfrac{dk}{d\omega}$ or $v = \dfrac{d\omega}{dk}$ (la vitesse de groupe) et donc au final :

$g(\omega) = \dfrac{L}{2\pi v}$

On met un facteur 2 devant pour prendre en compte les positifs et les négatifs et donc au final on a :

$g(\omega) = \dfrac{L}{\pi v}$

Ce résultat est juste selon le cours

-- En 2D

La densité d'état locale est de un état pour chaque surface de $\left\dfrac{2\pi}{L}\right^2$ et donc la densité locale est de

$g(k) = \dfrac{L^2}{4\pi^2}$

Comme en 1D on pose $g(k)dk = g(\omega)d\omega$ et donc $g(\omega) = g(k)\dfrac{dk}{d\omega}$

Donc, selon ce que je comprends, au aurait une densité 2D égale à :

$g(\omega) = g(k)\dfrac{dk}{d\omega}$

$g(\omega) = \dfrac{L^2}{4\pi^2}\dfrac{1}{v}$

Mais ce n'est pas juste selon le cours, on est censé trouver :

$g(\omega) = \dfrac{L^2}{2\pi}\dfrac{\omega}{v^2}$

Je ne vois pas les étapes pour arriver à ce résultat.
J'ai besoin de comprendre comment faire ce calcul car j'aurai un contrôle où je devrai le refaire, mais les étapes ne sont pas détaillées...

Merci d'avance pour votre aide

Posté par re : Calcul densité d'états de phonons en 2D 29-09-24 à 18:38

Bonjour,

Citation :
Comme en 1D on pose $g(k)dk = g(\omega)d\omega$

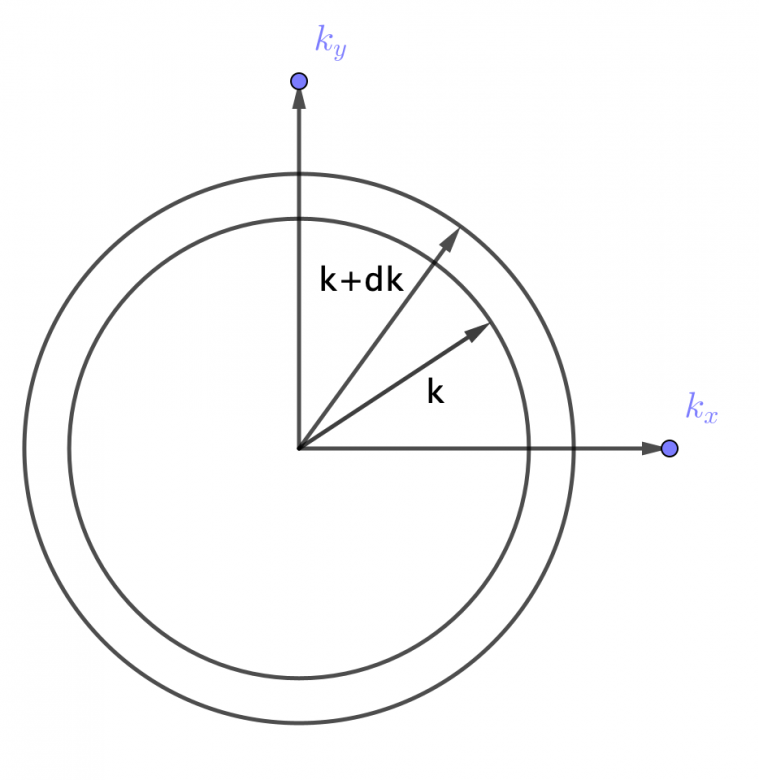
C'est là qu'est le problème, on est en 2 dimensions et donc le nombre d'états dN entre k et k+dk est g(k) fois la surface dans l'espace des k : celle entre le cercle de rayon k et celui de rayon k+dk.

On aura alors $dN=g(k)\times dS=g(\omega)d\omega$

$Calcul densité d\'états de phonons en 2D$

Posté par re : Calcul densité d'états de phonons en 2D 30-09-24 à 01:01

Bonsoir,

Merci gts2 ! J'ai pu trouver le résultat comme ça en prenant l'aire de l'anneau, ça fonctionne bien.

Juste pour ma compréhension : mon prof a dit qu'il fallait utiliser de l'intégration en coordonnées polaires, or je ne vois pas bien les étapes de calcul à faire.

Je sais qu'il faut utiliser le fait que $dS=dk_x.dk_y = kd\theta.dk$ , puis ensuite intégrer $g(k).dS$ seulement sur $\theta$ ... mais je ne comprends pas car si on intègre un côté de l'équation, il faut intégrer l'autre côté également. Donc à droite de l'équation on aurait

$\int_{\theta=0}^{2\pi}g(\omega)d\omega$

?? C'est juste un détail de démarche mathématique mais ça me bloque un peu

Même si on final on arrivait à intégrer à droite, on aurait plus la même chose, ce ne serait plus $g(\omega)$ qu'on aurait mais la densité "globale" (qu'on note $D(k)$ ). Donc au final ça n'est pas équivalent au calcul via l'aire de l'anneau...

Posté par re : Calcul densité d'états de phonons en 2D 30-09-24 à 07:57

On intègre uniquement sur θ, car à une pulsation ω correspond une norme k quelque soit le θ correspondant.

Explicitement le nombre N d'états est :
$N=\iint \dfrac{d k_x \cdot d k_y}{(2 \pi / L)^2}=\iint \dfrac{k d \theta \cdot d k}{(2 \pi / L)^2}=\int \frac{2 \pi k \cdot d k}{(2 \pi / L)^2}=\int g(\omega) d(\omega)$

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Calcul densité d'états de phonons en 2D

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique