Inscription / Connexion Nouveau Sujet
Calcul de trajectoires
Bonjour à tous,
J'ai un petit problème de physique que je n'arrive pas à résoudre. Je suis pourtant persuadé que la solution n'est pas si compliquée que ça, et pourtant elle m'échappe.
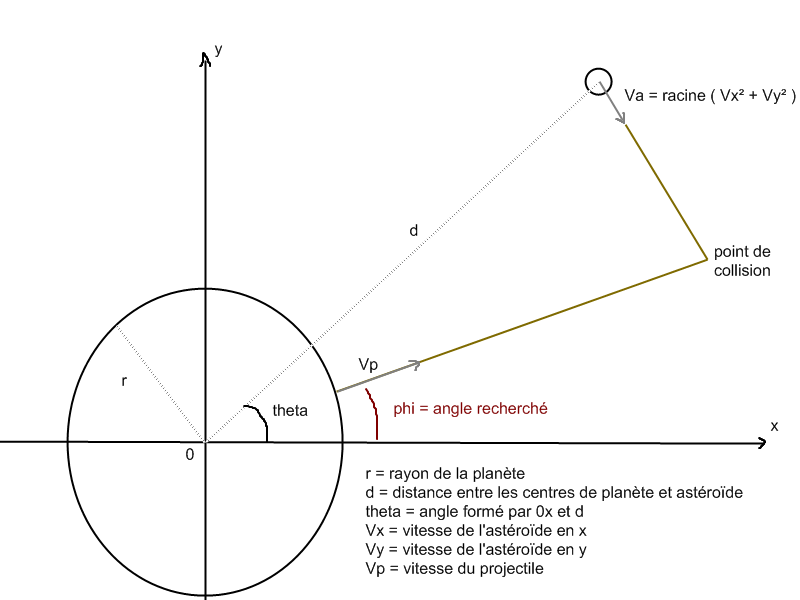
J'ai une planète à la surface duquel se trouve un puissant canon (qu'on estime mobile tout autour de sa circonférence). J'ai également un astéroïde que le canon doit détruire en tirant dessus. Problème : l'astéroïde est mobile. Sa vitesse est cependant constante, la gravité n'intervenant pas. La vitesse du projectile tiré par le canon est constante également. Je connais la distance de l'astéroïde au centre de la planète, et sur le repère passant par le centre de la planète, j'ai ses coordonnées et ses vitesses en X et en Y.
Selon quel angle phi tirer le projectile ?
J'ai réussi à déterminer cet angle dans le cas improbable où le rayon de ma planète est nul. Mais lorsqu'il faut faire jouer le rayon de celle-ci je sèche. Pourtant, si on visualise la solution de l'équation comme l'intersection d'une parabole avec une droite (dans un repère où abscisse = temps et ordonnées = distance à la planète), où la parabole est la distance de l'astéroïde par rapport à la planète et où la droite est celle de mon projectile, il suffit de faire partir la-dite droite en y = rayon de la planète pour x = 0 (puisqu'on tire à t0). Mais malgré ça, je n'y arrive pas. J'ai beau essayer en repère polaire ou cartésien, mais non, rien à faire.
Pouvez-vous m'aider ?
Bonsoir,
La vitesse de l'astéroïde constante ? La planète devrait la modifier mais si c'est une hypothèse du problème...
J'ai une solution mais je ne sais pas où ça mène parce que c'est compliqué.
Astéroïde
Projectile
et on fait
On a un système de 2 équations à 2 inconnues t et  .
.
On extrait t de la première par exemple et on injecte cette valeur dans la deuxième.
On n'a plus qu'une équation en  (pas forcément facile à résoudre).
(pas forcément facile à résoudre).
On trouve un cos( -
- ),
),  étant défini par sa tangente. Mais encore faut-il que ce cosinus soit compris entre -1 et +1 et, là, c'est peut-être moins simple...
étant défini par sa tangente. Mais encore faut-il que ce cosinus soit compris entre -1 et +1 et, là, c'est peut-être moins simple...
Bonsoir, et merci de participer.
J'avais eu une idée similaire qui me donnait deux solutions. J'avais des difficultés à déterminer laquelle est la bonne lorsque je me suis rendu compte que je n'avais pas pris en compte le rayon de ma planète. Du coup ça m'avait un peu découragé je dois avouer...
D'autre part il doit exister plusieurs cas de figure où le projectile ne peut pas toucher l'astéroïde (exemple : l'astéroïde s'éloigne de la planète plus vite que la vitesse du projectile). J'ai réussi à trouver comment savoir si la collision est possible ou pas, mais je ne sais pas comment ça va influer sur mon équation. Parce que ces cas de figure feront probablement que l'équation sera impossible à résoudre. Mais à quel niveau, j'ai du mal à le déterminer.
La collision n'est pas possible quand mon cosinus n'est pas compris entre -1 et +1, sans doute.
Je peux mettre le calcul mais le résultat est compliqué et je ne sais pas si c'est exploitable
Je veux bien y jeter un oeil parce que je n'ai pas tout compris du premier message.
Et puis si ça se trouve il n'y a pas de solution simple !
Par exemple je n'ai pas bien compris ce qu'est  qu'on utilise dans le cosinus. Peut-être de voir la démonstration m'aiderait à mieux appréhender le problème.
qu'on utilise dans le cosinus. Peut-être de voir la démonstration m'aiderait à mieux appréhender le problème.
C'est parti...
Astéroïde
Projectile
et on fait
Donc :
De la 1ère, on tire :
Dans la deuxième :
On peut aboutir, après quelques calculs, à :
En posant :
D'où :
Je ne suis pas allé plus loin pour l'instant mais on doit pouvoir trouver une condition pour avoir ou
Je crois que je commence à comprendre.
En fait  n'est pas là pour représenter un angle mais pour aider à simplifier l'équation tout en passant par un élément connu (et défini par tan
n'est pas là pour représenter un angle mais pour aider à simplifier l'équation tout en passant par un élément connu (et défini par tan ).
).
Ce qui fait qu'au final, si le cosinus est entre -1 et 1, alors on peut prendre acos de l'équation finale, à laquelle on ajoute atan de l'équation définissant tan , et on obtient alors la valeur de
, et on obtient alors la valeur de  . C'est sacrément complexe, mais je ne vois qu'une seule solution pour voir si ça fonctionne : calculer un ou plusieurs
. C'est sacrément complexe, mais je ne vois qu'une seule solution pour voir si ça fonctionne : calculer un ou plusieurs  prévisibles (grâce à certains cas particuliers) et voir si ça correspond. Si oui, il y a de grandes chances pour que l'équation soit bonne.
prévisibles (grâce à certains cas particuliers) et voir si ça correspond. Si oui, il y a de grandes chances pour que l'équation soit bonne.
Ah oui, alors tant que j'y suis voilà comment j'avais fait moi : j'avais au contraire tenté de définir t en fonction des autres données. Pour ce faire, j'avais commencé à passer certaines équation au carré afin de me retrouver avec des ( sin ² + cos
² + cos ² ), ce qui me permettait de remplacer le tout par 1 afin de ne plus avoir de
² ), ce qui me permettait de remplacer le tout par 1 afin de ne plus avoir de  nulle part. Ca m'a pris pas mal de temps, et quand j'ai vu que je n'avais pas pris en compte le rayon de la planète, j'ai craqué.
nulle part. Ca m'a pris pas mal de temps, et quand j'ai vu que je n'avais pas pris en compte le rayon de la planète, j'ai craqué.
Je vois que tu as compris...  est un angle "fictif" effectivement.
est un angle "fictif" effectivement.
Comme on demande  , j'ai préféré essayer de le garder.
, j'ai préféré essayer de le garder.
En fait, l'écriture semble complexe mais je n'ai pas utilisé autre chose que :
avec
Si tu arrives à montrer que le résultat est bon, tiens-moi au courant
Plutôt que de vérifier la solution j'ai commencé par essayer de suivre la démonstration jusqu'au bout en tâchant de comprendre tous les éléments et toutes les étapes, et c'est désormais chose faite. Je dois reconnaître que la démonstration est, sinon complexe, particulièrement ingénieuse, et je suis impressionné (mais peut-être parce que je ne connais pas assez bien ma trigonométrie :s).
J'ai donc vérifié la démonstration, et elle me semble théoriquement juste. Je vais maintenant faire les calculs afin de pouvoir vérifier ce que ça nous donne en fonction de la situation et savoir si l'équation fonctionne tout autour du cercle (la planète) en toutes circonstances (excepté les cas du cos( -
- ) non compris entre -1 et 1).
) non compris entre -1 et 1).
Merci beaucoup pour ton aide, elle m'a été très précieuse, surtout dans le sens où j'ai pu en tirer des enseignements qui pourront me resservir dans de nombreux autres cas de figure.
Je reviendrai poster lorsque j'aurais découvert ce que donne notre équation à rallonge une fois mise en pratique. Merci encore.
Comme je l'ai déjà dit, ce qui m'étonne un peu, c'est cette histoire de vitesse constante...
A ma connaissance, le seul cas où ça peut se produire, c'est une trajectoire circulaire autour de la planète (constante en norme, pas en direction bien sûr...).
Donc un cas qui doit être assez simple, c'est l'astéroïde sur une trajectoire circulaire autour de la planète.
Je confirme que la vitesse de l'astéroïde est constante dans le repère cartésien, la gravité de la planète étant inexistante (dans les hypothèses de départ du problème). Il n'est donc pas en orbite autour de celle-ci.
J'ai donc commencé les vérifications d'usage, et je suis visiblement tombé sur un os.
J'ai peut-être fait une erreur à un moment, alors je préfère poster ici mon calcul afin de comprendre si je me suis trompé, et si oui de quelle manière. Mais j'ai peur de ne pas avoir fait d'erreur et que l'équation ne fonctionne pas. Auquel cas, je ne vois vraiment pas d'issue au problème :s
Ah si, j'ai malgré tout relevé un point qui me travaille. J'ai remarqué qu'à un moment nous avions posé . Or il me semble que
, ce qui nous donne en réalité
.
Ne faudrait-il pas déterminer le signe de sec ?
?

OK pour les hypothèses du problème...
On a :
Donc, effectivement, il y a un qui devrait se promener...
Mais un angle défini par sa tangente est défini à  près. Comme
près. Comme  est un angle "fictif", on peut décider que
est un angle "fictif", on peut décider que .
peut être positif ou négatif et on a cos
 > 0 et sin
> 0 et sin > 0 ou < 0.
> 0 ou < 0.
Je regarde le calcul...
Comme un angle défini par sa tangente est défini à  près, il y a deux solutions :
près, il y a deux solutions :
°
et
°
La deuxième solution nous donne  = 0
= 0
Je reviens sur ce que j'ai écrit dans le message "Posté le 25-10-10 à 14:42". En fait, il y a deux solutions :
Ou on reprend la solution :
et, pour  , il y a deux solutions (message "Posté le 25-10-10 à 20:03").
, il y a deux solutions (message "Posté le 25-10-10 à 20:03").
Il reste un petit problème pour choisir la bonne solution. On peut dire que, manifestement, 106,26° n'est pas une bonne solution, vu la direction de .
Mais peut-on trouver un critère plus sûr pour trouver la bonne solution ?
En fait on a deux incertitudes sur le signe, une en cos( -
- ) et une seconde en
) et une seconde en  tout court.
tout court.
Il y a donc quatre solutions à chaque équations, et il s'agit par la suite de définir laquelle est la bonne. Quatre solutions, ça me rappelle un peu les quatre quarts du cercle en coordonnées polaires, de 0 à 2 . Mais peut-être que la direction de l'astéroïde compte également. A savoir s'il passe à gauche ou à droite de la planète.
. Mais peut-être que la direction de l'astéroïde compte également. A savoir s'il passe à gauche ou à droite de la planète.
C'est amusant, lorsque j'ai posté mon premier message, j'étais énervé, voire même abattu, mais maintenant, je suis excité de trouver comment faire fonctionner l'équation. Le résultat est à portée de main, c'est la dernière ligne droite. Hourra !
Je vais recommencer mon calcul en utilisant des symétries par rapport aux axes de mon calcul précédent. Ca permettra peut-être d'y voir plus clair.
Avant ça je viens de me rendre compte que sur les quatre solutions, il y en a deux qui sont identiques, et dans le cas de mon calcul, c'est la bonne réponse !
Il faut donc que je vérifie également si dans les quatre réponses il y en a toujours deux identiques, et si c'est toujours la bonne réponse. Si oui, alors il me faudra encore comprendre pourquoi, mais au moins, je l'aurai, ma solution !
Ne pas tenir compte de mon précédent message, j'ai bêtement oublié que ce n'était pas qu'une histoire de signe. Je vais donc m'en tenir aux symétries pour garder des cas simples et facilement calculables.
Oui, on peut considérer qu'il y a deux solutions pour :
et deux solutions pour  (angle défini par sa tangente donc à
(angle défini par sa tangente donc à  près).
près).
Ce qui en fait quatre... Mais je pense qu'elles se réduisent à deux parce qu'elles doivent être identiques deux à deux (à confirmer  ).
).
Il ne faut pas se décourager. La façon utilisée n'est pas forcément la meilleure (on peut toujours supposer qu'il en existe au moins une autre...) mais elle est obligatoirement bonne, même si le calcul ne paraît pas très simple.
Dans un domaine voisin, j'ai cherché une erreur pendant cinq jours et je viens de la trouver. J'étais persuadé que ce que j'avais écrit, était bon mais les résultats que j'obtenais, n'étaient pas logiques.
On a toutes les réponses d'ailleurs...
°
°
parce que
et :
°
° (==>
 +
+ )
)
On a quelque chose du type :
Donc les 4 possibilités :
°
°
°
°
Donc 4 solutions différentes !
D'après la direction de l'astéroïde, on voit que seul peut répondre à la question mais j'aimerais trouver un critère plus convaincant
 ...
...
J'ai trouvé un critère plus convaincant... C'est un peu long !
Pour chaque  , on calcule le t correspondant.
, on calcule le t correspondant.
Pour chaque t (ou chaque  ), on calcule xa et xp.
), on calcule xa et xp.
On a l'égalité xa = xp seulement pour  = 0 .
= 0 .
Il ne reste plus qu'à vérifier que ya = yp pour cette valeur de t (ou de  ).
).
C'est le cas, bien entendu...
Mais c'est bien sûr !!!
Il est évident qu'en lançant le projectile en  = 180° on n'a aucune chance qu'il percute l'astéroïde, à part en tirant à rebrousse temps (ce qui est "impossible" dans notre cas de figure). Sinon, en tirant à 106° ou 286°, ça ne correspond pas du tout au point de rencontre recherché entre l'astéroïde et le projectile. Il n'y a qu'une seule solution, et c'est bien celle qui permettra de faire coïncider les éléments de départ de l'équation, à savoir le couple (X, Y) du point de rencontre.
= 180° on n'a aucune chance qu'il percute l'astéroïde, à part en tirant à rebrousse temps (ce qui est "impossible" dans notre cas de figure). Sinon, en tirant à 106° ou 286°, ça ne correspond pas du tout au point de rencontre recherché entre l'astéroïde et le projectile. Il n'y a qu'une seule solution, et c'est bien celle qui permettra de faire coïncider les éléments de départ de l'équation, à savoir le couple (X, Y) du point de rencontre.
Formidable, nous avons donc au final un mode de calcul un peu complexe, mais totalement juste. Cher Marc35, tout le crédit de cet heureux dénouement est à mettre à votre compte, car vous m'avez été d'une précieuse érudition. J'ai été ravi de partager cet aventure physique et mathématique avec vous, et j'espère un jour pouvoir me retrouver à vos côtés de nouveau dans des circonstances similaires, sinon tout aussi passionnantes. Merci encore de m'avoir porté jusqu'au bout de cet étrange périple (les hypothèses vous ayant paru particulières dès le départ). Avec un intervenant comme vous sur un sujet, il n'est pas besoin d'en avoir de plus grand nombre !
Je repasserai sans doute pour vous montrer ce qu'il advient de mes prochains calculs résolus grâce à votre équation. Vous pourriez être surpris 
OK  ...
...
J'ai oublié de te féliciter pour ton français impeccable ainsi que l'orthographe. Cela devient de plus en plus rare de nos jours.
(D'autant qu'il est beaucoup plus facile de faire des fautes sur un écran que sur une feuille où on écrit "à la main"... enfin, en ce qui me concerne en tout cas).
Bonjour !
Je suis de retour avec un gros problème.
J'ai fait de nouveaux calculs avec de nouvelles valeurs de départ qui sont :
r = 50
d = 285
Vx = -0.13
Vy = -0.24
Vp = 1 (pour simplifier un peu)
 = 1.599 (en radians)
= 1.599 (en radians)
J'obtiens donc ceci :
 1 = acos( K ) + atan ( L )
1 = acos( K ) + atan ( L )
 2 = acos( K ) + atan ( L ) +
2 = acos( K ) + atan ( L ) + 
 3 = acos( -K ) + atan ( L )
3 = acos( -K ) + atan ( L )
 4 = acos( -K ) + atan ( L ) +
4 = acos( -K ) + atan ( L ) + 
Je calcule K, et je trouve 0.0938
Je calcule L, et je trouve -0.98
Je calcule donc mes quatre angles :
 1 = 0.7
1 = 0.7
 2 = 0.889
2 = 0.889
 3 = 3.84
3 = 3.84
 4 = 4.03
4 = 4.03
D'intuition, j'envisageais un  légèrement supérieur à
légèrement supérieur à  de l'ordre de 1.7. Je remarque qu'aucun
de l'ordre de 1.7. Je remarque qu'aucun  ne semble correspondre.
ne semble correspondre.
Alors je calcule les différents t.
t1 = -52.036
t2 = -52.3966
t3 = -47.135
t4 = -46.361
Puis, lorsque j'ai fait les calculs pour trouver Xa et Xp, j'ai constaté avec surprise que les deux valeurs étaient toujours identiques, quelle que soit le cas de figure (1, 2, 3, ou 4).
Par contre, pour les Ya et Yp, une autre surprise m'est tombée dessus. Ya vaut toujours à peut près pareil, et Yp aussi. Mais les deux valeurs ne coïncident jamais.
Je me demande si j'ai fait une erreur quelque part, malgré le fait d'avoir revérifié plusieurs fois. J'aimerai comprendre d'où vient mon problème. Ai-je fait une erreur ? Est-ce parce que l'astéroïde est passé dans le second quart de cercle et que l'équation doit alors changer ? Ou est-ce autre chose encore ?
J'ai l'impression que je ne vais pas réussir à m'en sortir, arf :s
J'ai refait les calculs et je trouve la même chose.
Mais je pense qu'on a oublié des solutions.
Je reviens un peu plus tard...
Mince alors, mais c'est vrai ça. Dans mon premier cas, très simple, on trouvait bien la solution, sauf que... le temps était négatif aussi. C'était donc peut-être un hasard total du à la simplicité des données de départ.
Dans le premier cas, il y a des temps négatifs et des temps positifs, en particulier, le "bon" temps qui est égal à 3 s.
Dans le deuxième cas, tous les temps sont négatifs ! Ceci signifie certainement qu'il n'y a pas de solution.
Je vais essayer de trouver un cas peu différent mais qui fonctionne...
C'était donc peut-être un hasard total dû à la simplicité des données de départ
Probable...
Il me semble qu'il existe des solutions, mais ce calcul ne les fournit pas. En effet, si on se représente un astéroïde à environ  /2 qui se déplace lentement en se rapprochant de la planète, et qu'on tente de l'intercepter avec un projectile se déplaçant plus rapidement (par rapport à l'astéroïde), il est possible que t soit grand (étant donné la distance à parcourir, de 235), sans doute de l'ordre de 190, mais sur mon schéma il semble clair qu'on pourra l'intercepter.
/2 qui se déplace lentement en se rapprochant de la planète, et qu'on tente de l'intercepter avec un projectile se déplaçant plus rapidement (par rapport à l'astéroïde), il est possible que t soit grand (étant donné la distance à parcourir, de 235), sans doute de l'ordre de 190, mais sur mon schéma il semble clair qu'on pourra l'intercepter.
C'est vraiment perturbant Ôo
Il y a un cas qui devrait toujours fonctionner.
C'est le cas où l'astéroïde démarre à  /2 avec vx = 0 et vy à une valeur négative. Autrement dit, l'astéroïde se précipite sur la planète par "le pôle nord" (par comparaison avec la Terre).
/2 avec vx = 0 et vy à une valeur négative. Autrement dit, l'astéroïde se précipite sur la planète par "le pôle nord" (par comparaison avec la Terre).
L'angle  est a priori
est a priori  /2, je pense...
/2, je pense...
Il semble que, si on trouve t < 0 avec la formule tirée de la 1ère équation, il faille tirer une expression de t avec la 2ème équation qui donnerait le résultat exact pour t.
Je l'ai vérifié sur une exemple.
Oui, il semble bien que ce soit ça...
Si on a t < 0 par la première équation :
On tire t de la deuxième :
Et t doit être positif.
On injecte cette valeur dans la première équation et on fait un calcul analogue pour trouver cos( -
- ).
).
J'ai fait le test avec les conditions que j'ai données :
 =
=  /2
/2
vx = 0
vy < 0
et on trouve le "bon"  (==>
(==>  =
=  /2)
/2)
Ce serait donc une question de demi-cercle ?
Le premier cas étant avec un  <
<  /2, peut-être le premier calcul est le bon dans le demi cercle de droite, et il faut inverser la procédure dans le demi-cercle de gauche !
/2, peut-être le premier calcul est le bon dans le demi cercle de droite, et il faut inverser la procédure dans le demi-cercle de gauche !
Je m'y remettrai demain, pour tester tout ça.
J'ai hâte d'en avoir terminé avec tout ce bazar !
Je ne connais pas la justification théorique de la chose mais, selon les valeurs de r, ,d,
,d, ,vx,vy,vp, il faut tirer t de la première ou de la deuxième équation de façon à prendre la valeur de t positive.
,vx,vy,vp, il faut tirer t de la première ou de la deuxième équation de façon à prendre la valeur de t positive.
S'il est positif avec la 1ère équation, il doit être négatif avec la 2ème et réciproquement. S'il est négatif dans les deux cas, c'est que le problème n'a pas de solution.
Astéroïde
Projectile
et on fait
Donc :
De la 2ème, on tire :
Dans la première :
On peut aboutir, après quelques calculs, à :
En posant :
D'où :
Dans l'exemple que j'ai choisi :
d = 1000
vx = 0
vy = -5
 =
=  / 2
/ 2
r = 50
vp = 3
==> cos( -
- ) = 0 ==>
) = 0 ==>  -
- = (
= ( /2) + k
/2) + k
 -
- = (
= ( /2) et
/2) et  = 0 ==>
= 0 ==>  =
=  /2
/2
Avec  =
=  /2 et vx = 0:
/2 et vx = 0:
Et :
sauf erreur éventuelle de recopie...
Ok, alors il est temps pour moi de montrer ce que ça donne et le pourquoi du comment. J'espère que l'anglais ne vous est pas trop étranger.
Voici ce que donne l'équation : http://games.verticea.fr/PlanetRescue/
Je pense que vous repérerez aisément où l'équation s'avère utile.
Vous remarquerez également que ça ne fonctionne pas pour les astéroïdes situés dans la moitié haute de l'écran. Il faut savoir qu'en Javascript (le langage utilisé ici), la moitié haute est celle située entre - et 0 (ce qui équivaut à être entre
et 0 (ce qui équivaut à être entre  et 2
et 2 il me semble). Je ne sais pas pourquoi ça ne fonctionne pas, mais je peux certifié qu'il ne s'agit pas d'une erreur de l'ordre de
il me semble). Je ne sais pas pourquoi ça ne fonctionne pas, mais je peux certifié qu'il ne s'agit pas d'une erreur de l'ordre de  , même si ça en a parfois l'air. En effet, même en ajoutant
, même si ça en a parfois l'air. En effet, même en ajoutant  au résultat lorsque l'astéroïde est dans la partie haute de l'écran, le canon tira bien vers le haut, mais rate systématiquement sa cible, tandis qu'en bas il accumule les headshots (en plein dans le mille).
au résultat lorsque l'astéroïde est dans la partie haute de l'écran, le canon tira bien vers le haut, mais rate systématiquement sa cible, tandis qu'en bas il accumule les headshots (en plein dans le mille).
Voilà, si vous avez la moindre question n'hésitez pas, je vous dois déjà une belle chandelle, et vous informe que vous serez crédité pour l'aide que vous m'aurez apporté dans ce projet qui est placé en Creative Commons By-SA (j'espère que vous savez de quoi il s'agit, sinon : http://creativecommons.org/licenses/by-sa/2.0/fr/ ). Pour l'instant, le crédit est le suivant :
"This function has been made with the help of Marc35 from the forum at ilephysique.net" à la ligne 179 du fichier functions.js ( http://games.verticea.fr/PlanetRescue/src/functions.js ).
Je peux le modifier si vous le souhaitez, comme je peux également retirer toute mention de votre existence.
Merci à vous.
Ok, alors il est temps pour moi de montrer ce que ça donne et le pourquoi du comment. J'espère que l'anglais ne vous est pas trop étranger.
Voici ce que donne l'équation : ![]()
Je pense que vous repérerez aisément où l'équation s'avère utile.
Vous remarquerez également que ça ne fonctionne pas pour les astéroïdes situés dans la moitié haute de l'écran. Il faut savoir qu'en Javascript (le langage utilisé ici), la moitié haute est celle située entre - et 0 (ce qui équivaut à être entre et 2 il me semble). Je ne sais pas pourquoi ça ne fonctionne pas, mais je peux certifié qu'il ne s'agit pas d'une erreur de l'ordre de , même si ça en a parfois l'air. En effet, même en ajoutant au résultat lorsque l'astéroïde est dans la partie haute de l'écran, le canon tira bien vers le haut, mais rate systématiquement sa cible, tandis qu'en bas il accumule les headshots (en plein dans le mille).
Voilà, si vous avez la moindre question n'hésitez pas, je vous dois déjà une belle chandelle, et vous informe que vous serez crédité pour l'aide que vous m'aurez apporté dans ce projet qui est placé en Creative Commons By-SA (j'espère que vous savez de quoi il s'agit, sinon : ![]() ). Pour l'instant, le crédit est le suivant :
). Pour l'instant, le crédit est le suivant :
"This function has been made with the help of Marc35 from the forum at ilephysique.net" à la ligne 179 du fichier functions.js ( ![]() ).
).
Je peux le modifier si vous le souhaitez, comme je peux également retirer toute mention de votre existence.
Merci à vous.
EDIT : j'ai ajouté les liens cette fois-ci.
Pas de problème, je lis et je parle l'anglais.
"Creative Commons By-SA" ==> Non, je ne sais pas ce que c'est.
"This function has been made with the help of Marc35 from the forum at ilephysique.net" à la ligne 179 du fichier functions.js" ==> Cela me va très bien.
Le canon semble ne pas se déplacer sur la partie supérieure de la planète. Il arrive que le canon tire vers un endroit où il n'y a rien (vers le bas), alors qu'il y a des astéroïdes dans la partie haute.
Il faut plus d'un projectile pour détruire un astéroïde. Si, pour le premier projectile, la position est bonne, pour les suivants, ce n'est plus le cas. Il faudrait donc refaire le calcul entre deux lancers de projectiles.
Il est difficile de savoir si les solutions trouvées pour le système d'équations couvrent absolument tous les cas.
Bonjour Marc35,
Comme je l'ai déjà dit à d'autres contributeurs IRL qui ont tenté (infructueusement) de parvenir à la solution de mon problème, il ne faut surtout pas prendre en compte ni les unités, ni l'aspect graphique du jeu.
En effet, les unités utilisés sont les mêmes partout, et puisqu'aucune constante universelle (comme la gravitation) ne vient interférer dans les calculs, ceux-ci pourraient être à partir de m.s-1 comme de km/h ou encore de toise par minute, le calculs serait juste dans tous les cas.
De même, ce n'est pas parce qu'on voit le canon se déplacer et essayer de toucher un astéroïde en tirant plusieurs fois dans sa direction qu'il faut prendre ceci en compte dans l'équation. En effet, à chaque  t (le jeu étant à 25Hz, le
t (le jeu étant à 25Hz, le  t vaut donc 40 millisecondes) notre canon s'oriente vers l'astéroïde le plus proche en tentant d'anticiper son mouvement. Ainsi, lorsqu'il a rechargé et tire, il est nécessairement déjà placé dans la bonne direction.
t vaut donc 40 millisecondes) notre canon s'oriente vers l'astéroïde le plus proche en tentant d'anticiper son mouvement. Ainsi, lorsqu'il a rechargé et tire, il est nécessairement déjà placé dans la bonne direction.
Le fait qu'un astéroïde ne soit pas détruit du premier coup ne change donc rien au calcul. Lorsqu'il est détruit et/ou qu'un autre astéroïde devient le plus proche de la planète, le canon se déplace pour aller viser l'autre astéroïde, tout simplement. Ca n'a aucune incidence sur la fonction mathématique permettant le calcul que nous effectuons.
En ce qui concerne les Creative Commons, c'est une licence indiquant que le logiciel peut-être modifié et redistribué librement, tant que les auteurs du travail original sont cités et que la redistribution se fait sous la même licence.
Lorsque l'astéroïde est en haut de l'écran (angle  négatif), j'avais l'intuition suivante : le canon se place en fonction de (
négatif), j'avais l'intuition suivante : le canon se place en fonction de ( +
+  ) et se décale dans le mauvais sens (à droite au lieu d'aller à gauche).
) et se décale dans le mauvais sens (à droite au lieu d'aller à gauche).
J'ai donc voulu vérifier cette hypothèse qui m'aurait grandement facilité la vie. J'ai donc ajouté le calcul suivant pour tout  négatif :
négatif :
 = (2 x
= (2 x  ) -
) -  +
+ 
Ce qui correspond à la solution dans le cas où mon intuition s'avérait vérifiée.
Eh bien ça ne fonctionne pas, mais c'est intéressant. Le canon anticipe un peu trop, et plus la trajectoire de l'astéroïde se rapproche d'une tangente à la planète, et plus ce décalage est accru. J'imagine qu'on doit pouvoir rectifier le tir d'une manière ou d'une autre, mais pour l'instant je ne m'y suis pas encore penché, par hâte de partager avec vous ce nouveau "résultat".
J'ai oublié de dire que bien évidemment, lorsque l'astéroïde fonce droit vers la planète, le décalage est nul et le canon tire bien sur l'astéroïde. Ce qui est étrange, c'est que dans les  positifs le décalage soit correct, mais dans les
positifs le décalage soit correct, mais dans les  négatifs, il semble deux fois trop grand.
négatifs, il semble deux fois trop grand.
D'où l'idée de diviser ce décalage par deux. C'est du bricolage, mais bon.
Et étrangement, c'est presque parfait !
Je ne me l'explique pas (encore), mais c'est pas loin de fonctionner. Il y a cependant quelques ratés, alors qu'il n'y en a pas vers le bas (il y a des tirs perdus, mais c'est parce que le canon est en plein déplacement, il n'a pas encore rejoint le bon angle de tir).
Démonstration ici : ![]()
Oui, effectivement, vers le haut, il y a quelques soucis...
Il faudrait déjà savoir pourquoi, dans certains cas, il faut prendre t dans une équation et, dans d'autres cas, il faut prendre t dans l'autre équation.
A priori, il n'y a pas de justification théorique. Si on trouve un temps négatif, on prend l'autre... Normalement, dans un système de deux équations à deux inconnues, on peut le faire dans n'importe quel ordre et on obtient le même résultat. Il est vrai qu'il ne s'agit pas tout à fait d'un système de deux équations à deux inconnues mais d'un système de deux équations à trois inconnues : t, cos , sin
, sin . On contourne le problème en utilisant une relation entre deux inconnues (cos
. On contourne le problème en utilisant une relation entre deux inconnues (cos et sin
et sin ) pour le ramener à deux inconnues. Mais il est vrai que cos
) pour le ramener à deux inconnues. Mais il est vrai que cos et sin
et sin ne sont pas indépendants pour un
ne sont pas indépendants pour un  donné.
donné.
Mais cette façon de faire induit peut-être des phénomènes secondaires qui conduisent aux résultats constatés.
Je n'ai pas inventé cette méthode. Cela s'utilise pour résoudre des équations du genre a cos x + b sin x = 0 ou même a cos x + b sin x = c .


