Inscription / Connexion Nouveau Sujet
Calcul d'un champ électrique par la loi de Coulomb
Bonjour, il s'agit de calculer le champ électrique créé en un point M par une sphère chargée en surface
Soit une sphère de rayon R de charge surfacique 
de centre O, je note r la distance de M par rapport à O
Si je prends un anneau élémentaire de la sphère perpendiculairement à OM, toutes les charges sont à équidistance de M.
Mais le rayon de cet anneau n'est pas R mais R' compris entre 0 et R, et son centre n'est plus O mais O', et la distance de ces charges à M est
et voilà je ne sais pas du tout comment m'y prendre. Donc je schématise mon raisonnement ... :
http://i43.tinypic.com/qss9ps.png
Je suis perdu, ça fait toute l'après-midi que je suis dessus.. un indice svp ? merci...
Il y a une erreur sur l'image dans le texte bleu, c'est a priori Etotal=Qcos(theta)/(2pi*epsilon*(O'M²+R'²))
et pas 4*pi
et mon problème principal c'est que je ne suis pas sûr des bornes des intégrales, ni des déplacements infinitésimaux (dO'M et dR' ?), sans compter que mon raisonnement ne marche que pour une demi-sphère, et donc je me demande si je ne suis pas sur une mauvaise piste... (enfin si mon raisonnement est juste je pourrais faire en sorte de faire un raisonnement similaire pour l'autre partie de la sphère, mais ça me parait bizarre quand même)
(en fait il n'y avait pas d'erreur je crois)
Bon, après un autre essai j'obtiens une formule plus propre, en remplaçant cos(Θ) par O'M/sqrt(O'M²+R'²) :
Champ généré par l'anneau élémentaire en un point M tel que O'M soit perpendiculaire au plan contenant l'anneau
La formule est homogène donc que je ne pense pas m'être trompé...
Maintenant il ne reste plus qu'à les additionner, et c'est là que je bloque... car O'M devrait varier de r-R à r et R devrait varier de 0 à R déjà pour une demi-sphère, mais donc il faudrait que j'intègre ma formule doublement entre ces bornes, or pour obtenir ma formule j'ai déjà fait une intégrale (c'est un anneau donc dimension 1, donc pour obtenir le champ généré par la sphère, surface, je devrais normalement n'avoir à intégrer qu'une fois puisque si j'intègre deux fois quelquechose à 1D ça me calculerait un volume...)
C'est trop facile avec le théorème de Gauss, donc on a pas le droit de l'utiliser.
On est obligé d'utiliser la loi de coulomb, qui n'est vraiment pas pratique...
Merci quand même
dommage car par intégration c'est nettement plus dur
on considère un "anneau élémentaire" (en bleu sur le dessin) entre O et O + dO
sa charge est: dQ = 2
R 2 sinO dO
le champ E est dirigé selon (Oz) (je te laisse justifier)
dEz = 1/4
o dQ/ PM2 cos a
dEz = R2/2o . sin O dO/PM2 . d/PM
dEz = R2/2o . d sinO dO/PM3
avec PM = 
(R2sin2 O + d2)
et d = z - R cosO
donc Ez = 
O dEz = ...
tu tombes sur une intégrale en O plutot lourde
c'est là qu'on voit la puissance de theoreme de Gauss 
sauf erreur
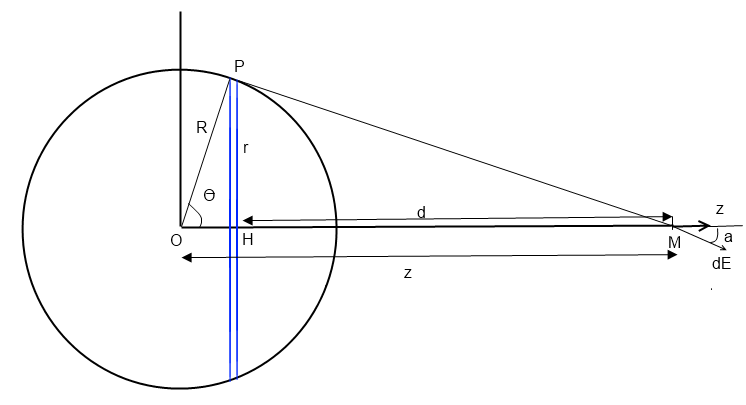
>le champ E est dirigé selon (Oz) (je te laisse justifier)
ça c'est bon, merci
Si j'ai bien compris, O=theta
et l'intégrale à la fin va de 0 à pi
merci beaucoup !! je vais essayer de me débrouiller pour calculer l'intégrale.
Annuler
connectez vous