Inscription / Connexion Nouveau Sujet
Calcul champ magnétique
Bonjour,
je bloque sur cet exercice,
4 fils de cuivre supposés infinis sont disposés sur les arêtes d'un parallélépipède rectangle à section carrée ABCD. Chacun d'eux est parcouru par un courant dont le sens est donné sur le schéma en annexe
1) ) Etablir les champs magnétique en ABDC créé respectivement par quatre fils au centre 0 du carré. O
2) En déduire le champ magnétique qui en résulte
Merci !
Bonjour,
Explique ce que tu as été capable de faire et ce qu'éventuellement tu ne comprends pas. L'aide qui pourra ensuite t'être apportée sera plus efficace !
Tu dois bien connaître tout de même l'expression du vecteur champ magnétique B créé par un conducteur rectiligne infiniment long parcouru par un courant !
Oui,
mais ce qui me gêne c'est qu'ils soient crées au centre du carré.
Comment évaluer cette distance d ?
Je n'ai aucune valeur numérique ...
Une source de champ magnétique - un conducteur rectiligne parcouru par un courant par exemple -crée un champ magnétique dans tout l'espace qui l'entoure. On pourrait donc définir un vecteur champ magnétique B en n'importe quel point de l'espace ! Ici, pour simplifier, on demande de déterminer le vecteur champ seulement au centre du carré. Dans la formule que tu écris, d désigne la distance entre le point où on calcule le champ (ici le point O) et l'axe du conducteur cylindrique qui crée le champ.
Attention : il faut aussi réfléchir à la direction et au sens du vecteur champ en fonction du sens du courant...
Revois bien ton cours sur tout cela... Le raisonnement est assez proche de celui déjà fait sur le vecteur champ électrique, même si les deux champs ont des propriétés assez différentes.
Je n'ai aucune valeur numérique ...
Tu notes I l'intensité du courant continu commune aux 4 fils et a la longueur d'un côté du carré. Tu va obtenir une expression littérale de B qui fera intervenir µo, I et a.
Bonjour,
Tu raisonnes comme si les quatre vecteurs champs étaient colinéaires !
Il faut vraiment que tu revois ton cours ! Le schéma ci-dessous pourra peut-être t'aider...
Remarque : je ne suis pas sûr que la distance d = OA soit égale à a 2...
2...
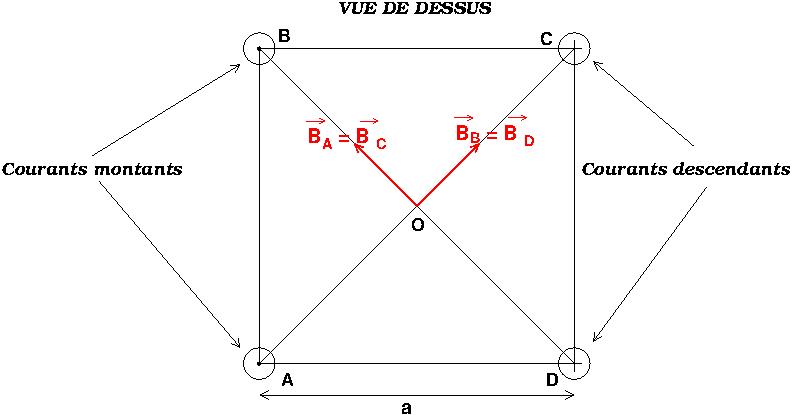
Remarque : je ne suis pas sûr que la distance d = OA soit égale à aV2...
Moi je suis sûr que tu es sûr que ce n'est pas cela.

Pourquoi B_A = B_C ? je ne comprend pas ...
Les courants circulent en sens inverses dans les deux fils. Pour les directions : revois la règle de l'observateur d'Ampère ou la règle du tire-bouchon de Maxwell ou la formule donnant le vecteur B à l'aide d'un produit vectoriel... Les méthodes ne manquent pas !
d'accord je pensais justement que vu que les courants circulent en sens inverse, les champs étaient inversé :/
Mes calculs sont-ils correctes ou pas ?
Mes calculs sont-ils correctes ou pas ?
Ok pour la distance OA. En revanche, je n'ai rien vu concernant la direction, le sens et la norme du vecteur champ résultat. Il n'est évidemment pas nul !
heu....je n'ai pas vu comment calculer un champ résultant :/
logiquement je me suis dit qu'il fallait faire la somme
Ne me dis pas que tu ne sais déterminer une somme de quatre vecteurs qui, de plus, sont égaux deux à deux !
bin si, faut additionner leur coordonnées afin d'avoir les coordonnées du résultat
u(x,y) et v(x',y') --> w=x+y = (x+x';y+y')
mais là j'ai aucune coordonnées


