Inscription / Connexion Nouveau Sujet
Bulle d'air remontant à la surface
Bonjour à tous 
,
Voilà un énoncé que l'on me propose:
Un plongeur se trouve au fond d'un lac et expulse une bulle d'air par un tuyau.
La bulle détachée du tuyau remonte jusqu'à la surface libre du lac. On observe cette bulle pendant un intervalle de temps suffisamment court pour que sa vitesse de remontée U soit constante, ainsi que son rayon R.
On estime que les forces de frottement dues à la viscosité peuvent être négligées dans cet écoulement si Re 
10.
1) Calculer l'ordre de grandeur de ce nombre de Reynolds si la vitesse de la bulle est de l'ordre de 10 cm/s, et son rayon de l'ordre de 5 mm. On prendra pour la viscosité de l'eau 
= 10-3Pa.s.
2) Que peut-on en conclure ? Quel théorème peut-on alors utiliser pour relier pression, vitesse et altitude dans l'écoulement d'eau autour de la bulle ?
Ensuite, on nous présente la figure 1 attachée ci-dessous.
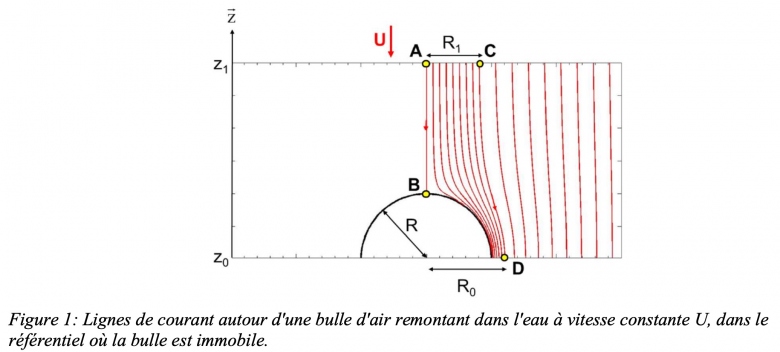
On souhaite maintenant calculer la vitesse de remontée U de la bulle en fonction de son rayon R. Pour cela, on se place dans le référentiel où la bulle est immobile et l'eau se déplace avec une vitesse U loin en amont de la bulle (Fig. 1). On a représenté sur la Fig. 1 les lignes de courant de l'écoulement stationnaire autour de la bulle, vues en coupe dans un plan de symétrie vertical passant par le centre de la bulle. On considère deux lignes de courant distinctes. La première est située sur l'axe de symétrie, elle passe par le point A et par le point B situé sur l'avant de la bulle. L'autre ligne de courant passe par le point C et le point D proche de l'équateur de la bulle. Aux points A et C, situés loin de la bulle, la vitesse de l'eau est U et la pression est pA = pC = p1.
3) Que vaut la vitesse de l'eau au point B? Justifier la réponse.
4) On note U0 la vitesse de l'écoulement au point D. On fait l'hypothèse que la bulle est sphérique, ce qui implique que pB=pD=p0. Déterminer l'expression de la vitesse de l'écoulement au point D.
Sur la Fig. 1, les lignes de courant permettent de visualiser la diminution de la section de passage de l'écoulement d'eau, due à la présence de l'obstacle que constitue la bulle. Le tube de courant qui s'appuie sur la ligne de courant CD a une section d'entrée circulaire de rayon R1 à la cote z1. A la cote z0, cette même ligne de courant se trouve à une distance R0 de l'axe de la bulle. On suppose que dans la section du tube de courant située à la cote z0, la vitesse de l'écoulement est approximativement uniforme, égale à U0.
5) Quelle quantité est conservée entre les sections du tube de courant ? En déduire l'expression de la vitesse U en fonction de la vitesse U0, de R1, de R0 et de R, rayon de la bulle.
Pour la question 1;
J'ai la formule suivante:
avec U la vitesse, D le diamètre,
la viscosité et 
la masse volumique.
Ici est-ce normal que l'on nous donne toute les données sauf la masse volumique de l'eau?Est-ce que c'est parce que ça n'inclut pas vraiment sur l'ordre de grandeur du nombre de Re?
J'ai pris comme valeur = 1026 kg/m3, c'est la valeur que l'on nous donne à l'exercice d'après pour l'eau de mer.
J'ai donc:
Re = 1026*0,1*0,01/0,001 = 1026
Est-ce correct?
Pour la question 2:
D'après l'énoncé, on observe cette bulle pendant un intervalle de temps suffisamment court pour que sa vitesse de remontée U soit constante. L'écoulement est donc stationnaire.
Par contre j'ai un peu de mal, conceptuellement quant à la preuve que l'écoulement est isovolume. Je sais bien qu'il faut utiliser le fait que le rayon R de la bulle est constant. Mais faut-il dire que le volume autour de la bulle est constant? Ou le volume d'air à l'intérieur de la bulle est constant?
Enfin, on a un Re = 1026 >> 10 donc , d'après l'énoncé, les frottements visqueux peuvent être négligés. L'écoulement est donc parfait.
Vu que l'écoulement est stationnaire, isovolume et parfait, on peut appliquer le théorème de Bernoulli pour relier pression, vitesse et altitude dans l'écoulement d'eau autour de la bulle.
Est-ce bien correct?
Pour la question 3
A et B sont sur la même ligne de courant, on applique le théorème de Bernoulli.
On a:
Est-ce bien correct?
Pour la question 4:
Je me suis tout d'abord demandé si je pouvais réutilisé les résultats des questions précédentes pour répondre à celle-ci mais je n'ai pas trouvé comment. Je ne sais pas s'il faut les réutiliser.
J'ai donc appliqué le théorème de Bernoulli comme à la question 3:
C et D sont sur la même ligne de courant.
Est-ce bien correct?
Pour la question 5:
Je pense qu'il faut utiliser la conservation du débit volumique dans le tube de courant. Cependant, je ne suis pas sûr quand à la justification de cette conservation du débit volumique. Est-ce suffisant de dire que l'écoulement est isovolume?
Avec la conservation du débit, on a:
Est-ce bien correct?
Ce qui m'a un peu troublé en faisant cette exercice, c'est le fait que l'on utilise pas toujours les résultats des questions précédentes pour avancer. C'est peut-être parce que je l'ai mal résolu ^^
Bonjour
Je réponds d'abord à tes questions d'ordre génral, je vérifierai tes calculs par le détail après.
1° : concernant la masse volumique de l'eau : même un non physicien sait quelle est d'environ 1kg/L soit environ 103kg/m3.
2° : sauf cas très particulier, les liquide sont considérés comme incompressible : masse volumique indépendante de la pression.
Bonjour,
1- Le fait que l'on ne vous donne pas la masse volumique de l'eau ne me parait pas vraiment un problème...
2- Isovolume se réfère à l'eau (plus exactement à l'écoulement de l'eau, mais pour un liquide quasi incompressible, ce n'est pas un problème), cela n'a rien à voir avec le volume de la bulle. L'écoulement d'un liquide incompressible est isovolume. Sinon, d'accord pour la conclusion.
3- La variation de pression dans l'eau sur 5mm de hauteur est quand même négligeable. Ce qui compte ici est la forme des lignes de courant, que peut-on dire de la direction de la vitesse en B ? Que conclure ?
4- C'est correct, mais vu la remarque précédente, vous devez (?) pouvoir négliger le terme de pesanteur.
5- Faute de frappe 2ème équation à gauche : il manque 
R12. Idem à droite : parenthèses mal placées ?
3)
La vecteur vitesse en B est parallèle à la ligne de courant AB. Cependant, je ne vois pas vraiment ce que je peux en conclure ^^
Quelle est la direction de la vitesse vis-à-vis de la surface de la bulle ?
***Edit gbm : bonjour gts2, juste pour info, tu as fait un post-croisé avec vanoise 
. Bon après-midi***
Le régime permanent (indépendant du temps) impose la conservation du débit massique. Puisque la masse volumique est supposée fixe (fluide incompressible), on obtient aussi la conservation du débit volumique.
Bonjour,
***Edit gbm : bonjour gts2, juste pour info, tu as fait un post-croisé avec vanoise . Bon après-midi***
Je laisse vanoise poursuivre.
Bonjour à tous,
@gts2 : il n'est pas interdit d'interagir avec vanoise pour aider Jawad0610, il faut juste le faire méthodiquement pour éviter de rendre sa compréhension plus délicate si des messages sont postés en // par chacun de vous . Pour apporter un complément d'information ou une méthode alternative après coup par exemple.
Je vous laisse poursuivre, bon après-midi printanier à vous tous !
Bonjour gbm, bonjour gts2
gts2, nouveau sur ce forum, n'a peut-être pas remarqué la possibilité de vérifier l'absence de nouvelle réponse en cliquant sur la ligne rouge en dessous de l'icône "poster" ;
Cela dit, je partage à 100% le point de vue de gbm publié dans son message de 14h29. Pour sans convaincre, il suffit de jeter un coup d'œil sur un autre forum où de nombreux intervenants postent sans même se donner la peine de lire attentivement les messages précédents. Cela vire rapidement à la cacophonie et tant pis celui qui demande de l'aide.
gts2 s'est manifestement plus investi que moi sur ce post. Je le laisse continuer.
Avec deux contributeurs, il ne m'est pas plus compliqué de comprendre. Au contraire
C'est vrai quand les messages sont coordonnés, c'est à dire tiennent compte de ce que l'autre a écrit...
Je me demande s'il y a un théorème en particulier à utiliser pour la vitesse en B. Je crois comprendre d'après vos remarques que l'on a pas besoin d'appliquer le théorème de Bernoulli.
Bonjour,
Ce n'est pas vraiment un théorème, mais que peut-on dire de la vitesse à l'interface d'un fluide parfait et d'un "solide" ?
Autre piste : dessinez les lignes de courant avant et après B, et utilisez la définition d'une ligne de courant.
Correction sur ce que j'ai dit : en fait les vitesse sont toutes petites et le terme de pesanteur joue.
On utilisera Bernoulli mais après avoir déterminé vB.
Bonjour gbm, bonjour gts2
gts2, nouveau sur ce forum, n'a peut-être pas remarqué la possibilité de vérifier l'absence de nouvelle réponse en cliquant sur la ligne rouge en dessous de l'icône "poster" ;
Cela dit, je partage à 100% le point de vue de gbm publié dans son message de 14h29. Pour sans convaincre, il suffit de jeter un coup d??il sur un autre forum où de nombreux intervenants postent sans même se donner la peine de lire attentivement les messages précédents. Cela vire rapidement à la cacophonie et tant pis celui qui demande de l'aide.
gts2 s'est manifestement plus investi que moi sur ce post. Je le laisse continuer.
Oui, ça arrive, c'est la raison pour laquelle je me suis permis d'intervenir, pour éviter les incompréhensions :
12 ans après, il m'arrive encore d'oublier de le faire
Je vous laisse poursuivre,
Bon après-midi,
En fait, je n'ai pas encore abordé dans le cours les interfaces fluides-solides. C'est pour ça que je ne comprenais pas vraiment où vous vouliez en venir.
En cherchant sur internet, j'ai trouvé que, pour un écoulement parfait, la composante de vitesse normale à la paroi d'un "solide" est nulle.
La vitesse de l'eau en B est donc nulle.
Est-ce bien cela?
C'est bien cela. Si vous n'avez pas vu les interfaces, la ligne de courant qui arrive en B est vertical et les lignes qui repartent sont horizontales, lignes pour lesquelles v est tangent; Le seul vecteur qui soit à la fois vertical et horizontal est le vecteur nul.
Je comprends, merci.
Concernant la 4:
4- C'est correct, mais vu la remarque précédente, vous devez (?) pouvoir négliger le terme de pesanteur.
Correction sur ce que j'ai dit : en fait les vitesse sont toutes petites et le terme de pesanteur joue.
Dois-je donc changer mon résultat pour la question 4 ou est-il correct ainsi?
D'accord
Concernant la 5, je tiens à m'excuser, j'ai fait n'importe quoi en recopiant ce que j'ai fais.
Donc en utilisant ce que vanoise a indiqué sur la conservation du débit massique. On a la conservation du débit volumique.
On a:
Par contre, que vouliez-vous dire par :
parenthèses mal placées ?
Les parenthèses sont toujours aussi mal placées : pourriez-vous énoncer en français la signification de la surface que vous cherchez à calculer et en particulier à quel moment apparait la différence ?
J'essaye de calculer la surface de la section de sortie du tube de courant étudié. En z0, celui-ci est délimité par la paroi de la sphère et la ligne de courant C-D.
J'ai donc cherché la distance entre la paroi de la sphère et D, cela me donne le diamètre (et non le rayon, je l'ai considéré comme le rayon dans mon calcul) de la section de sortie du tube de courant.
La distance est R0 - R.
On a donc:
La surface de section de sortie du tube est donc:
Vous calculez la surface du disque de diamètre R0-R.
Voir le dessin ci-dessous : vue de dessus.
Quelle surface devez-vous calculer ?
Ce que j'essaye de calculer, c'est la surface du cercle en noir qui représente la section de sortie du tube de courant. (Mes excuses pour la piètre qualité).
Le rayon de ce cercle en noir est (R0-R)/2
Oui, c'est bien cela que vous calculez, et l'eau en provenance de passe où ?
Et donc quelle est la surface à calculer
D'après la figure 1, je dirais que l'eau en provenance de R12 passe dans à travers cette section représenté par le cercle noir. Il faut donc calculer sa surface.
Il faudrait un dessin 3D, mais là je ne suis pas au point.
La figure 1 est une coupe verticale de la bulle, lorsque vous parcourez la section d'entrée , le point C décrit un cercle, et D idem.
Les traits bleus radiaux sont les traces des lignes de courant de l'eau vues de dessus.
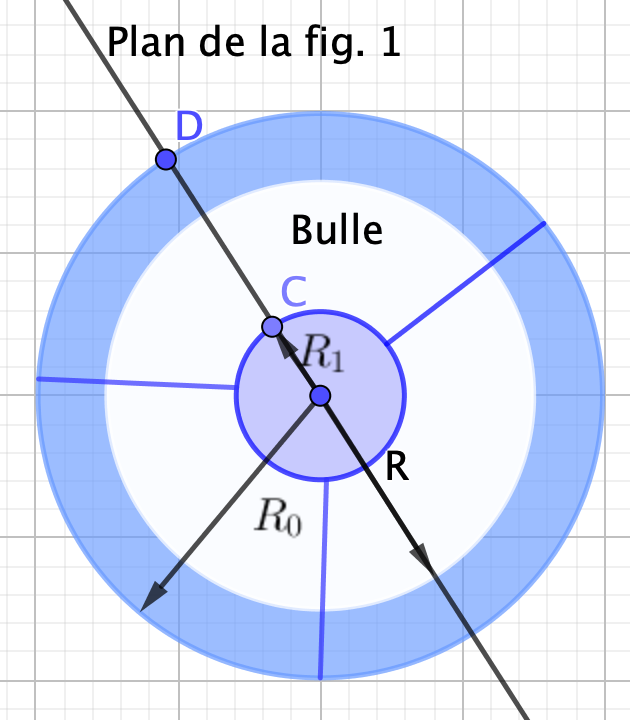
Je suis d'accord.
Pour la surface de la section d'entrée, qui est un cerclé décrit par le point C, on a bien R12.
Je fais donc de même pour le cercle débit par D, qui n'est pas la surface en bleu mais plutôt la surface que j'avais indiqué en noir. C'est pour cela que je détermine le rayon du cercle en noir.
J'ai précisé mon dessin : l'eau qui part de C' passe en D', qui part de C'' passe en D'' ...
Donc l'eau qui passe dans passe dans quelle surface ?
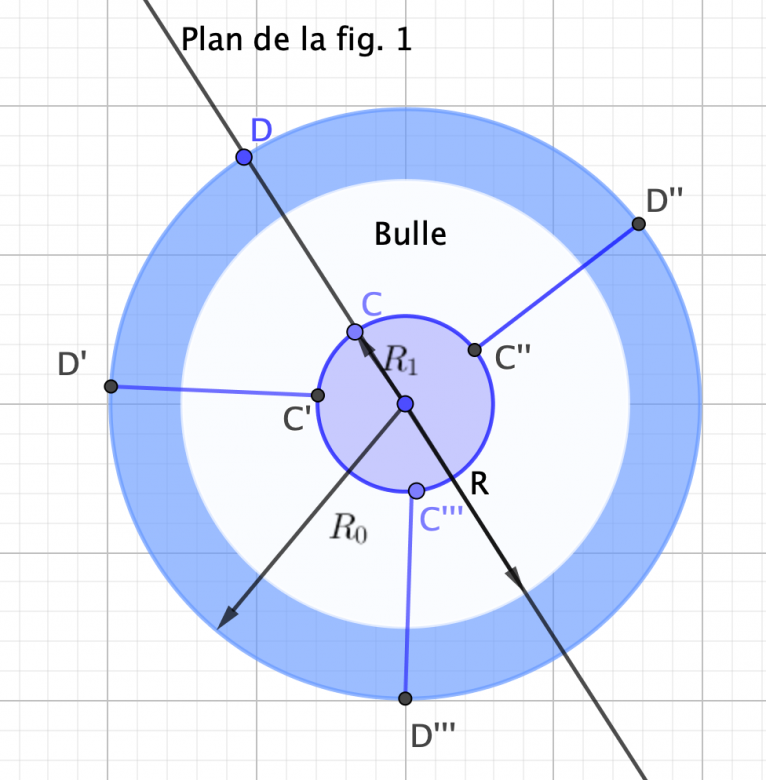
En prenant en considération ce dernier message, l'eau provenant de R12 passerait à travers toute la surface en bleu.
Bonjour,
Pour la question 1, pensez-vous qu'il faudrait que je dise que Re <2000 implique que l'écoulement est laminaire?
Pour la rédaction de la question 3:
"On remarque que la ligne de courant arrivant en B est verticale tandis que la ligne partant de B est horizontale. Le vecteur vitesse est toujours tangent à la ligne de courant. En B, le seul vecteur qui est à la fois horizontal est vertical est le vecteur nul. La vitesse en B est donc nul"
Pensez-vous que c'est rigoureux?
Bonjour,
Pour la question 1, on ne vous demande pas de commenter.
Le commentaire arrive en 2 et en lien "avec quel théorème peut-on alors utiliser ?". Donc le commentaire doit justifier ce alors, et ce commentaire est dans le texte "les forces de ... viscosité peuvent être négligées ... si Re>10. "
Merci, et concernant la rédaction de la question 3 ?
Pour la rédaction de la question 3:
"On remarque que la ligne de courant arrivant en B est verticale tandis que la ligne partant de B est horizontale. Le vecteur vitesse est toujours tangent à la ligne de courant. En B, le seul vecteur qui est à la fois horizontal est vertical est le vecteur nul. La vitesse en B est donc nul"
Pensez-vous que c'est rigoureux?
Annuler
connectez vous