Bonsoir,

Je ne sais pas si ça va t'aider grandement, ton problème est assez original...

Ton exercice me fait penser à l'étude des trajectoires coniques des corps célestes, avec pour origine du mouvement le centre du Soleil qui est donc le foyer de la conique.

On a souvent l'habitude de passer en coordonnées polaires (r, ) et d'utiliser le moment cinétique de point se déplaçant, ou encore, comme tu l'as dit, utiliser la conservation de l'énergie mécanique...

Mais dans ce genre de cas, on n'a affaire qu'à une seule force à considérer : l'attraction du Soleil.
(Et toi, t'en a deux ! P et R !)

Ceci dit, on aboutit à l'équation polaire d'une conique : r = p/(1+e.cos )

avec :
Si e = 1 : parabole
Si e < 1 : ellipse
Si e > 1 : hyperbole


Idée peut-être à creuser...


Et je te rassure, en passant en dynamique du solide, ça n'arrangera rien, tu vas devoir vraisemblablement faire intervenir le moment d'inertie de ta boule ! Donc considérer qu'elle a une énergie cinétique de translation ET une énergie cinétique de rotation...

En tout cas, "bon courage"...

2 cas :

a) La boule glisse sans rouler.

On doit connaître les conditions initiales, par exemple en y = yo la vitesse est vo
En prenant l'origine des énergies potentielles nulles au sommet (qui est ici un creux) de la parabole d'équation y = x², on a l'énergie mécanique de la boule : Em = mgyo + (1/2).m.vo²

Lorsque la bille est à une ordonnée y, on a : Em = mgy + (1/2).m.v² (avec v la vitesse instantanée de la bille au passage en cette position)

Sans perte par frottement, on a conservation de l'énergie mécanique et donc :  mgyo + (1/2).m.vo² = mgy + (1/2).m.v²

v² = vo² + 2g(yo - y)
v² = vo² + 2g.(yo - x²)

Comme y = x²
dy/dt = 2x.dx/dt
v² = (dy/dt)² + (dx/dt)² = (4x² + 1).(dx/dt)²

vo² + 2g.(yo - x²) = (4x² + 1).(dx/dt)²

On peut traiter cette équation avec un tableur par petits incréments de temps.

Un exemple traité de cette manière :
Avec comme données : vo = 0,1 m/s, yo = 1m, on trouve le graphe de la vitesse horizontale de la bille en fonction du temps (pour un simple "gauche-droite) :



-----
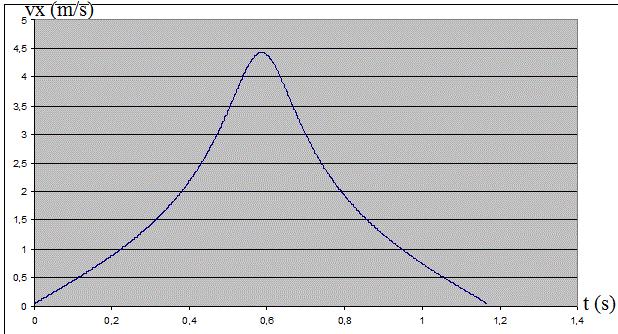
b) la bille roule sans glisser (quel que soit son rayon, même tendant vers 0)

Ici, on doit prendre en compte non seulement l'énergie cinétique de translation de la bille mais aussi son énergie de rotation autour d'un de ses axes de symétrie.

Si le G (centre d'inertie de la loule) a une vitesse v, la bille tourne autour d'un se ses axes de symétrie à la vitesse w = v/R (R = rayon de la bille)

L'énergie cinétique de translation est E1 = (1/2).m.v² et l'énergie cinétique de rotaion est E2 = (1/2).J.w² avec J le moment d'inertie de la boule autour d'un de ses axes de symétrie.

Si la boule est pleine et homogène, on a J = 2mR²/5 (autre chose si la boule n'est pas pleine bien entendu).

On a donc E2 = (1/2).J.w² = (1/2).(2mR²/5).v²/R² = mv²/5

Ec totale = E1 + E2 = (1/2).m.v² + mv²/5 = (3/5).m.R²

Et donc, la conservation de l'énergie mécanique s'écrit alors : mg.yo + (3/5).m.vo² = mgy + (3/5).m.v²

La suite est analogue au cas a mais en remplaçant, le (1/2) par (3/5) ...

On remarquera que le rayon de la bille est absent de l'équation différentielle et que donc celle-ci est valable même si R tend vers 0.
-----
On peut, en écrivant correctement le programme dans le tableur, modifier les conditions initiales à loisir et même en sophistiquant un peu introduire d'autres paraboles que la simple d'équation y = x².

On peut aussi, essayer d'ataquer la résolution de l'équation différentielle mathématiquement mais cela est sans réel intérêt "physique".


Je n'ai rien relu comme d'habitude.

Bonsoir à tous les deux,

Tout d'abord merci pour vos réponses.

Ensuite toutes mes excuses à JP, il est vrai que j'ai oublié les conditions initiales, en fait dans ma tête c'était compris dans le "hypothèse la plus idéale possible" : on la lâche en un point de la parabole d'ordonné y0 sans vitesse initiale.
Pour ce qui est de l'équation que tu obtiens, j'ai la même, et je vois que tu es confronté au même problème que moi : la résoudre est difficile.
La résolution approchée par le tableur, bien que satisfaisante pour le problème physique, ne me suffit pas : il me faudrait l'équation temporelle de x ou vx pour que je puisse la passer au plot ...
Néanmoins, petit hasard bienvenue, on a commencé les équa diff ce matin en math. Même si forcement on commence par les jolies équations linéaires, je me suis renseigné et il s'avère que l'on fera un peu de quadratique, au cas par cas quoi.

"On peut aussi, essayer d'ataquer la résolution de l'équation différentielle mathématiquement mais cela est sans réel intérêt "physique"." -> c'est bien mon problème, c'est le côté math qui m'intéresse... Je me suis peut être trompé d'île finalement.

Heroes : je n'avais pas pensé à l'analogie avec les mouvements à force centrale, c'est peut être à creuser en effet. Je vais voir ce que me donne le TMC par exemple.

Encore merci pour vos réponses très détaillées !

Bonne soirée.

Tu écris "Au fait, ce que je cherche est la vitesse horizontale de la boule"

Mais tu négliges de dire en fonction de quoi.

Du temps ? ou bien de l'abscisse de la position de la boule ?
---
Si c'est en fonction du temps, on est amené à résoudre l'équation différentielle (qu'elle qu'en soit la manière).

Si c'est en fonction de l'abscisse de la position de la boule, alors c'est facile, à partir de :

vo² + 2g.(yo - x²) = (4x² + 1).(dx/dt)² on peut en tirer directement (dx/dt) en fonction de x.

   Pour répondre à ta question, plus générale, sur les équations non linéaires en physique.
A priori pour les résoudre, on ne sait pas faire grand chose (pas de structure d'espace vectoriel, la plupart du temps pas de fonction usuelle adpatée, et j'en passe).
   Dans certain cas, on peut se ramener à une équation à variable séparable. Pour cela, il faut mieux partir d'une équation du premier ordre (en faisant un raisonnement énergétique, ou en multipliant le PFD par x' et en intégrant, ce qui revient au même) Ici, si je reprends l'expression donnée par J P, qui est déjà de la forme voulue (equa diff non linéaire du premier ordre) :

vo² + 2g.(yo - x²) = (4x² + 1).(dx/dt)²

tu peux réecrire la solution sous la forme :

dx * f(x) = dt

   Ensuite en intégrant f (c'est là l'étape difficile), tu obtiens t en fonction x. Il te faut ensuite chercher la fonction inverse, pour avoir ta solution explicite qu'aime les étudiants habitués aux problèmes à solution "exacte" .

   Je te donne un autre exemple que j'avais essayé de traiter il y a quelque années, qui rejoins ton interrogation. Tu prends un anneau, astreint à se déplacer sur un axe. Tu l'attaches à un ressort, fixé à l'autre extrémité. Si la longueur à vide est exactement la distance entre l'axe et l'autre extrémité du ressort, tu obtiens un potentiel en x^4. Si tu cherches à résoudre explicitement l'équation du mouvement, tu tombes sur une intégrale de la forme 1/sqrt(1-x^4), difficile à calculer.
   Idem pour le pendule, etc.

   Maintenant avec un ordinateur, tu peux calculer numériquement ton intégrale, et avoir la solution de toute équation pas trop compliqué.