Bonjour
La figure est celle fournie par l'énoncé  ? Bizarre... les bobines de Helmholtz sont deux bobines plates identiques et de même axe de symétrie.  Rien à voir avec un solénoïde...

Non, il n'y a pas de figure fournie pour l'énoncé. J'ai fais la figure selon l'énoncé de la question 1. Je crois que les questions sur les bobines de Helmholtz sont la 2 et 3.

Question 1 :

Ha oui ! Je n'avais pas compris cela.

Donc :

Est ce correcte ?

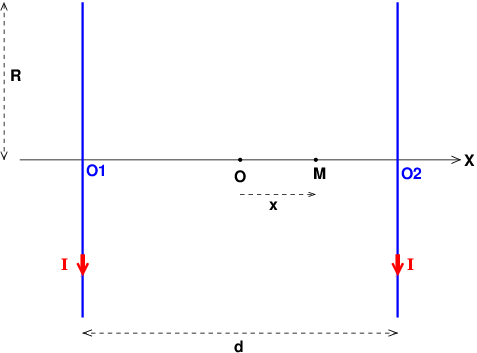
Oui sous réserve d'une orientation correcte du courant par rapport au sens positif de l'axe (Ox). Un scan du schéma serait le bienvenu...

Voila le schéma que j'ai fais.

Il vous semble bon ?

Pouvez vous m'aider pour la question 1.b s'il vous plait ?

Il faut, comme demandé par l'énoncé, faire intervenir la variable u=x/R.
Tu dois avoir étudié en cours de math la notion de point d'inflexion... Ce va t'amener à exprimer la dérivée première puis la dérivée seconde de B par rapport à la variable u.
Pour ton schéma, difficile de juger car on ne distingue pas clairement la partie avant de la partie arrière de la bobine. De plus, l'épaisseur de la bobine est négligeable. Quelle est la signification sur ton schéma du "L" ?

Bonjour, j'ai fais la dérivé seconde et j'ai trouvé comme points d'inflexions : x1 = R/2 et x2 = -R/2.
Le L que j'ai mis ne sert à rien en effet.

Pour la question 2 je ne comprend pas trop, qu'est ce que veux dire à l'ordre 4 ? Je penses qu'il faut que je calcul le champ créé par ses deux bobines plates mais je ne sais pas quoi faire ensuite.

Franchement, résoudre cet exercice sans plus d'indications fournies par l'énoncé... dur, dur à ce niveau ! Tu considères donc les deux bobines identiques parcourues par des courants de même intensité et de même sens (voir figure qui représente une vue de dessus des bobines).

Compte tenu de l'étude faite avec une seule bobine, le vecteur B créé par une seule bobine en un point M de son axe a pour expression :

avec : et D : distance du centre de la bobine au point M.

En t'aidant de la figure, tu vas donc pouvoir exprimer la somme des deux vecteurs champ créés par les bobines en fonction de Bo,R, d et x :



avec : B=f(x), l'expression faisant intervenir aussi les constantes Bo, d, R.

Tu connais la formule de Taylor :



L'étude de la parité de la fonction devrait te conduire à éliminer immédiatement les termes impairs. Imagine maintenant que tu arrives à démontrer que, pour une valeur particulière de d s'exprimant simplement en fonction de R :



Tu pourrais ainsi considérer que la valeur de B est très peu différente de la valeur au centre O, et cela au quatrième ordre près. En pratique, pour cette valeur particulière de ”d”, le vecteur champ est pratiquement égal au vecteur champ en C dans tout le volume à l'intérieur du cylindre dont les deux bobines constituent les bases. C'est tout l'intérêt des bobines de Helmholtz...

Bonjour, merci pour toutes ces explications et ce schéma !
Est ce que cela vous semble logique si je trouve d = R ?
Mais du coup je n'est pas besoin de faire la dérivé troisième ni la dérivé quatrième ?

Et si j'ai bien compris à l'intérieur entre les deux bobines avec d = R le champ est constant ?

La dérivée seconde, calculée en x=0, s'annule effectivement pour d=R.
Reprends l'expression de f(x) que tu as obtenue : tu vas constater que la fonction f est paire : f(x)=f(-x) ; conséquence : tous les termes d'ordre impairs doivent être absents du développement limité de Taylor. La dérivée première et la dérivée troisième sont donc nulle en x=0.
La dérivée quatrième en x=0 n'est pas nulle et les dérivées d'ordre 6,8,10... ne le sont pas non plus mais tous ces termes sont très petits devant f(O) de sorte qu'il est possible en bonne approximation de considérer B comme pratiquement constant le long de l'axe (Ox) entre les deux bobines. Le calcul de ces dérivées non nulles n'est pas demandé : l'énoncé demande seulement de montrer que B est constant le long de l'axe (Ox) au quatrième ordre près en x....

Quand on s'éloigne un peu de l'axe de symétrie (Ox) des bobines, à la distance ”r” de cet axe, on démontre que le vecteur champ est la somme de deux vecteurs champ ;
1° : un vecteur champ axial égal au vecteur champ le long de l'axe :


2° : un vecteur champ radial :



Puisque ici, la composante axiale ne varie pratiquement pas en fonction de x, la composante radiale est nulle ; le vecteur champ au voisinage de l'axe de symétrie est donc égal au vecteur champ le long de l'axe et celui-ci est constant...

A titre d'illustration, voici trois cas de bobines identiques et coaxiales décalées de la distance "d". En bleu : les courbes B/Bo créées par chaque bobine. Ce sont deux courbes identiques à celle étudiée à la question 1 mais décalée horizontalement  de -d/2 pour l'une et de +d/2 pour l'autre. En rouge : le rapport B/Bo du champ créé par l'ensemble des deux bobines (somme point par point des deux courbes bleues).
Pour d<R : on obtient un maximum de B en x=0 ;
Pour d>R : on obtient un minimum de B en x=0 ;
Pour d= R : B est pratiquement constant pour x compris entre -d/2 et +d/2...

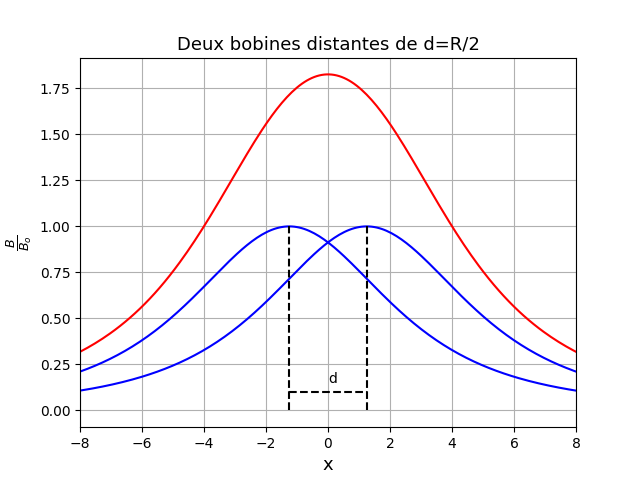
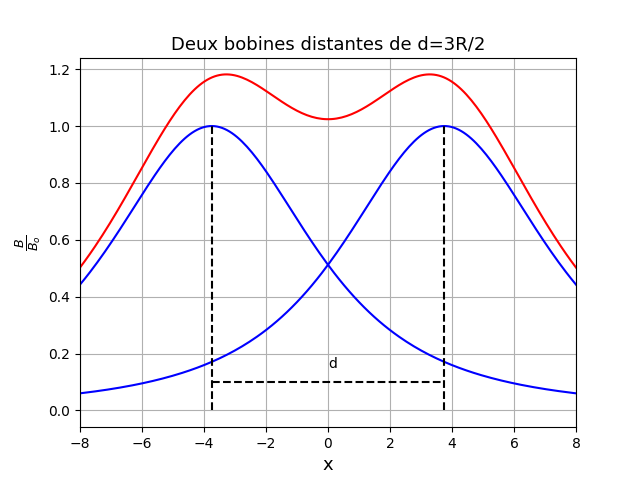
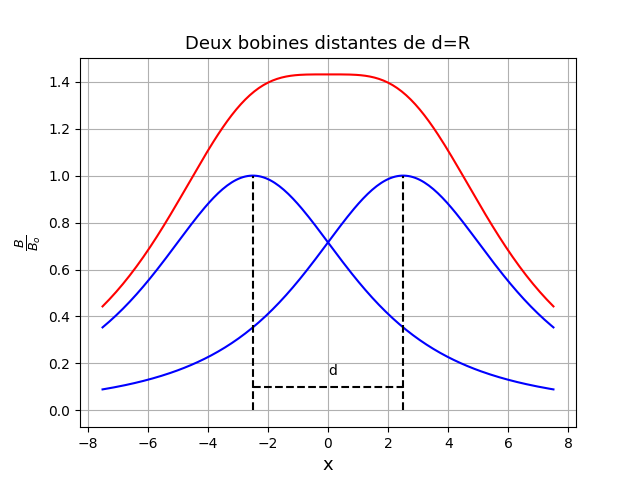
Bonjour, je vous remercie grandement ! je n'avais pas pensé à faire B/Bo pour les courbes je ne voyais alors pas trop comment faire. Ca me parait beaucoup plus claire on voit bien grâce aux courbes ce qu'il se passe en fonction de d pour le champ et voit donc bien que pour d = r le champ est presque constant entre les deux bobines.

Merci beaucoup, encore une fois, pour toutes ces informations et explications.