Inscription / Connexion Nouveau Sujet
bille en mouvement dans un fluide
Bonjour, j'ai pour la rentré, à rendre un DM de physique, malheureusement je bloque sur une partie d'un exercice, que voici;
Une boule de masse m de rayon R est reliée à un point fixe O par une tige de longueur ℓ, de masse négligeable par rapport à m, et de dimensions latérales négligeables. L'ensemble est en rotation autour de l'axe horizontal Oz, et reste donc dans le plan Oxy. Ce dispositif baigne dans un fuide, qui est en rotation solide, avec une vitesse angulaire constante Ω, autour de l'axe horizontal Oz. On note η la viscosité newtonienne du fuide et ρ sa masse volumique.
Le fuide exerce sur la boule une force de frottement visqueux →−Fv = −6πηR →v , où →v est la vitesse de la boule par rapport au fuide. On considérera que la grandeur m′ = m− 4/3 πρR^3 est strictement positive
(sujet d'oral de Centrale PC 2016)
La première question consiste à trouver l'équation différentielle vérifiée par θ(t). Voilà ce que j'ai trouvé:
l'énoncé nous donne une partie de l'équation, en fait on devait trouvé les coefficient devant le sin etc..
2e question, les éventuelle position d'équilibre et leurs condition d'existence, je trouve:
à condition que
avec \alpha le coefficient devant le sinus
ensuite, on doit vérifier leurs stabilité et c'est ici qu'il semble y avoir un problème:
j'utilise la méthode énergétique avec l'énergie potentielle et le travail et je trouves:
or si je remplace par
je trouve
, or cette chose ne s'annule jamais donc il ne peux pas s'agir d'un équilibre stable, ce qui est ici contre-intuitif. (si je suis mon intuition je penses qu'il faudrait trouver un cosinus au lieu d'un sinus… mais je ne vois pas comment)
Ensuite on néglige le therme convectif et on considère l'équation différentielle suivante:
on se place dans deux cas:
1e cas: 0<Oméga<alpha
on doit trouver le "temps caractéristique de retour à l'équilibre stable", doit on linéariser le sinus? je ne comprend pas bien comment débuter..
2e cas: Oméga>alpha
Donner la période T sous la forme d'une intégrale, je n'ai jamais trouvé de période sous forme d'intégrale, je ne sais pas non plus comment démarrer
On nous fournit l'équivalant suivant:
lorsque a tend vers 1-
Voila ensuite je dois pouvoir vérifier mes résultat avec un programme python
Peut etre mon équa dif est fausse puisque je n'ai jamais eu a faire avec la variable m' introduite dans l'énoncé..
Voila si vous avez des petites idées de comment avancer ou si vous avez trouvé des erreurs faites moi signe!
Merci bcp
Bonsoir
Si on note (R+l) et pas seulement l le rayon de la trajectoire du centre de la boule, on obtient bien l'équation différentielle que tu as indiquée.
Tu as effectivement un problème avec l'énergie potentielle : tu as oublié l'énergie potentielle associée à la force d'entraînement :
Lors d'un déplacement élémentaire , le travail élémentaire de cette force a pour expression :
Ce travail élémentaire apparaît comme une différentielle :
à une constante arbitraire près que l'on peu choisir nulle. Il faut ajouter cette énergie potentielle à celle de pesanteur.
Je te laisse rectifier la suite en conséquence.
Remarque : tu peux arriver au même résultat en posant mais il faut connaître l'expression du gradient en coordonnées polaires...
Un peu d'aide pour la suite.
doit on linéariser le sinus?
Je pense que oui car cette équation différentielle n'admet pas de solution exacte... A moins qu'un "indice" supplémentaire traîne quelque part dans l'énoncé complet...
je n'ai jamais trouvé de période sous forme d'intégrale
La méthode est un "classique" pour déterminer numériquement la période d'un pendule dans le cas des amplitudes d'oscillations importantes. Je parle bien de résolution numérique car, là aussi : pas de solution exacte.
Ici, la période est la durée d'un tour ; il suffit donc de partir de la vitesse angulaire et d'en déduire :
Il te suffit d'intégrer en choisissant bien les bornes...
Bonsoir et merci de m'avoir répondu!
Effectivement après avoir remplacer par mon je trouve bien une dérivée d'énergie potentielle nulle, formidable.
Je pensais enfaite qu'il n'y avait pas d'énergies potentielles pour les forces de ce types là, que je n'ai jamais vu auparavant d'ailleurs.
Pour ce qui est de la deuxième partie, je suis tenté de remplacer le sinus par un qui me gênera moins, dans l'équa dif. Qu'en pensez vous?
En ce qui concerne la période T sous forme d'intégrale, je vais faire des recherches..
Merci encore!
Merci encore pour votre aide!
Avec du recul j'ai effectivement déjà rencontré cette méthode "classiques" pour retrouver la 3e loi de Kepler en intégrant une Aire…
Bonne soirée!
Je n'ai lu qu'en diagonale ... mais il y quand même quelque chose qui me turlupine.
Si l'énoncé donne la masse volumique du fluide et précise aussi que : la grandeur m' = m− 4/3 πρR^3 est strictement positive....
... Je m'étonne alors que l'équation que tu trouves n'en tienne pas compte.
Je mettrais ta tête à couper que dans la réflexion, il faut remplacer le poids de la boule par
avec
la poussée d'Archimède du fluide sur la boule.
... Cela devrait mener à remplacer m par m' dans l'équation.
Remarque indépendante : si on mentionne un angle (theta) sans l'avoir défini, ce n'est pas très "sain", par exemple où est l'origine de la mesure ? et ...
Sauf distraction. 
Bonjour, en effet j'ai négligé la poussé d'Archimède, cela règlerait ce petit problème de m'.
En revanche, le theta est définie dans l'énoncé, du moins par le dessin qui montre clairement l'origine de la mesure, mais je l'ai qd même redéfinis dans ma copie.
Il me reste un dernier problème avec le temps caractéristique, je le trouve en fonction de alpha est non de Oméga. D'après l'équation différentielle simplifiée, on a: , mais d'après la méthode graphique je trouve:
. Je ne sais que faire de ces expressions..
Merci!
Pour ne pas négliger la poussée d'Archimède, il suffit de remplacer m par m' dans l'expression de  , pas dans l'équation différentielle du mouvement : le terme en
, pas dans l'équation différentielle du mouvement : le terme en fait toujours intervenir m et non m'. Cela ne change rien au reste du problème.
Je pensais enfaite qu'il n'y avait pas d'énergies potentielles pour les forces de ce types là, que je n'ai jamais vu auparavant d'ailleurs.
Une force conservative est une force soit de vecteur constant soit une force dépendant des paramètres de position, ce qui est le cas ici puisque le vecteur
Une force non conservative est une force qui dépend aussi de la vitesse ; exemple : les forces de frottement.
Pour la constante de temps ; je ne vois pas quoi faire d'autre que de poser sin(
 )
)
 , ce qui suppose la boule peu éloignée de sa position basse... Dans ce cas, la solution de l'équation différentielle du premier ordre fait intervenir une exponentielle de la forme
, ce qui suppose la boule peu éloignée de sa position basse... Dans ce cas, la solution de l'équation différentielle du premier ordre fait intervenir une exponentielle de la forme  est la constante de temps. De quelle méthode graphique parles-tu exactement ?
est la constante de temps. De quelle méthode graphique parles-tu exactement ?Bonjour,
Je retiendrai cette histoire de force conservative à l'avenir, merci.
Pour ce qui est de tau, j'ai fait posé dans l'équa diff: avec tau=1/alpha.
Mais l'énoncé demande ensuite que devient ce temps lorsque ?
Pour la méthode graphique, j'ai simplement tracé et on sait que lorsque t=tau, alors
Mon message d'hier à propos de la possibilité ou non de remplacer sin( ) par
) par  :
:
A moins qu'un "indice" supplémentaire traîne quelque part dans l'énoncé complet...
Tu viens de le fournir : puisque, par la suite, l'énoncé demande d'étudier le cas où
 tend vers
tend vers  par valeur inférieure, il faut envisager le cas où
par valeur inférieure, il faut envisager le cas où  tend vers
tend vers  /2. Cela exclut donc l'approximation initialement envisagée ! Je pense que tes professeurs te l'ont déjà conseillé : il faut toujours lire l'intégralité d'un énoncé avant de commencer à rédiger un problème. Les dernières questions fournissent souvent des indications directes ou indirectes concernant les premières .
/2. Cela exclut donc l'approximation initialement envisagée ! Je pense que tes professeurs te l'ont déjà conseillé : il faut toujours lire l'intégralité d'un énoncé avant de commencer à rédiger un problème. Les dernières questions fournissent souvent des indications directes ou indirectes concernant les premières .
Dans ces conditions, on voit bien intuitivement, compte tenu de l'étude préalable des positions d'équilibre que, si
 tend vers
tend vers  par valeur inférieure,
par valeur inférieure,  tends vers
tends vers  /2 au bout d'un temps très long, ce qui conduit à envisager une constante de temps qui tend vers l'infini quand
/2 au bout d'un temps très long, ce qui conduit à envisager une constante de temps qui tend vers l'infini quand  tend vers
tend vers  par valeur inférieure.
par valeur inférieure.
A partir de là, on peut envisager de chercher à résoudre l'équa. diff. en séparant les variables comme dans le second cas en posant :
Je ne comprends pas la logique de ton énoncé : aucun renseignement sur cette intégration n'est fournie dans le premier cas
 <
< ...
...
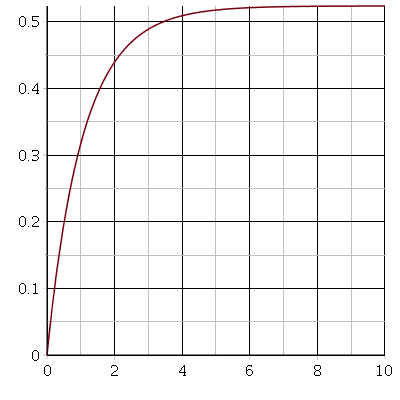
Pour comprendre ce qui se passe, à défaut d'une résolution plus rigoureuse voici deux simulations numériques, la première avec
 =
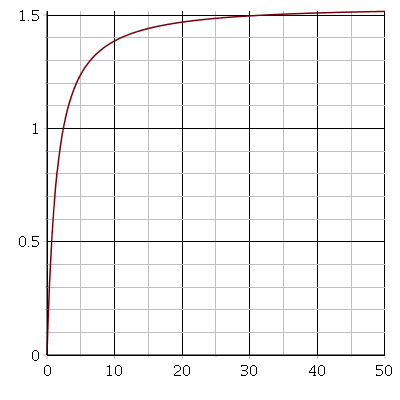
= /2 ; la seconde avec
/2 ; la seconde avec  =0,999.
=0,999. .
.
L'échelle des temps (abscisses) est arbitraire dans la mesure où je n'ai pas de valeurs numériques mais note bien qu'elle est dilatée d'un facteur 5 dans le second cas, par rapport au premier. En ordonnée :
 exprimé en radians.
exprimé en radians.
D'accord j'ai compris,
pour l'intégration, j'intègre le temps entre 0 et tau, pour l'angle entre 0 et pi/2=Arcsin(1), malheureusement l'équivalant fourni n'est valable que pour des bornes entre 0 et 2pi.
tanpis, intuitivement j'ai écrit:
cela devrait suffire
Pour le deuxième cas, il suffira de laissé le résultat sous forme d'intégrale, c'est ce qui est demandé de toute manière.
Les simulations numériques montrent bien que, lorsque Oméga est proche de alpha (par valeur inférieure), la bille met bien plus de temps à revenir vers sa position d'équilibre pi/2.
Attention : la position d'équilibre n'est pas toujours  /2.
/2.
 e = arcsin(
e = arcsin( /
/ ) comme tu l'as montré au début. Par exemple, pour ma première simulation avec
) comme tu l'as montré au début. Par exemple, pour ma première simulation avec  =
= /2 :
/2 :  e=
e= /6 rad
/6 rad
Concernant ton intégrale : la solution que tu fournis n'a pas de sens dans le cas  >
> . Selon mes sources (ne me demande pas la démonstration !) :
. Selon mes sources (ne me demande pas la démonstration !) :
si k>1. D'autres expressions équivalentes mais tout aussi simples (  ) sont possibles.
) sont possibles.


