Inscription / Connexion Nouveau Sujet
Bernoulli
Bonsoir, j'ai des questions préliminaires à un TP de physique et j'aimerais avoir votre aide :
1. Expérimentalement, on mesure la positon d'un objet à deux dates : x(t) et x(t+
t). Comment déduit-on la vitesse v moyenne entre t et t+t ?
2.Si les positions sont connues avec une incertitude 
x et qu'on peut négliger l'incertitude sur t, quelle incertitude v a-t-on sur la vitesse ?
3. Le récipient ci-dessous se vide par un orifice de diamètre d. Le jet sortant a une vitesse v. Par conservation du débit, quel est le lien entre dh/dt et v ?
4. La formule de Toricelli donne la vitesse du jet : . Montrer que dv/dt est constant pendant la vidange.
J'ai commencé en disant que :
1. v = [x(t+Δt)-x(t)]/ Δt
Après je ne sais pas s'il vaut mieux noter v = x/t pour être en cohérence avec la 2ème question.
2. J'hésite sur l'incertitude
Je sais que mon niveau est faible, mais je vous remercie énormément d'avance pour l'aide que vous pouvez m'apporter.
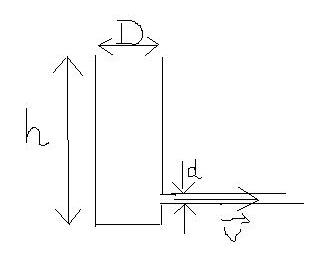
Je suppose que le récipient est cylindrique de diamètre D.
Et le tuyau de sortie à section citculaire de siamètre d.
débit de sortie d'eau = v * S(tuyau) = Racinecarrée(2gh) * Pi * d²/4
Et on a=
d(V contenu du réservoir)/dt = - débit de sortie d'eau
dVolume /dt = - Pi * d²/4 * Racinecarrée(2g*h(t))
*****
Pi.D²/4 * dh/dt = - Pi * d²/4 * Racinecarrée(2gh)
dh/dt = - Racinecarrée(2gh) * (d²/D²)
dh/dt = -(d²/D²).v(t)
*****
dh/dt = -Racinecarrée(2gh) * (d²/D²)
dh/racine(h) = -(d²/D²).Racinecarrée(2g) *dt
2 * racine(h) = -(d²/D²).Racinecarrée(2g) * t + K
Si Ho est la hauteur d'eau en t = 0 , on a : K = 2.racine(Ho)
2 * racine(h) = -(d²/D²).Racinecarrée(2g) * t + 2.racine(Ho)
racine(h) = -(d²/(2D²)).Racinecarrée(2g) * t + racine(Ho)
h(t) = [racine(Ho) - (d²/(2D²)).Racinecarrée(2g) * t]²
*****
dh/dt = -2.[racine(Ho) - (d²/(2D²)).Racinecarrée(2g) * t] * (d²/(2D²)).Racinecarrée(2g)
dv/dt = racine(2g) /(2.racine(h)) * dh/dt
dv/dt = - racine(2g) /(2.[racine(Ho) - (d²/(2D²)).Racinecarrée(2g) * t]) * 2.[racine(Ho) - (d²/(2D²)).Racinecarrée(2g) * t] * (d²/(2D²)).Racinecarrée(2g)
dv/dt = - racine(2g) * (d²/(2D²)).Racinecarrée(2g)
dv/dt = - 2g * (d²/(2D²))
dv/dt = - g.d²/D²
*****
Toutes erreurs incluses, je n'ai rien relu. 
je vais forcer de comprendre, mais est-ce que ma vitesse est bonne aussi ?
Et quid de la question 2 stp ?
Pourquoi dV/dt = - débit de sortie d'eau ?
(Avec ici V le volume dans le réservoir)
N'est ce pas évident ?
Débit = volume d'eau qui sécoule par unité de temps.
debit = [Volume(t) - Volume(t + Delta t)] / Delta t
debit = -[Volume(t + Delta t) - Volume(t)] / Delta t
et cela reste vrai si Delta t --> 0, donc :
débit = - dV/dt
-----
Sauf distraction.
Pourquoi doit-on s'intéresser au cas où t ---> 0 ?
Est-ce que tu peux me corriger pour la formule de la vitesse et me donner une piste pour l'incertitude (q° 1 et 2) afin que je n'ai pas la honte de me tromper là-dessus ?
Merci d'avance
v = [x(t+Δt)-x(t)]/ Δt
Ca c'est la vitesse moyenne entre les instants t et t+delta t et c'est ce qui est demandé dans la question 1
---
Mais si on veut la vitesse instantanée à un instant t on doit faire tendre le Δt vers 0
v(t) = lim(Δt --> 0) [(x(t+Δt)-x(t))/ Δt] et ca c'est la définition de la dérivée, on écrit cela v(t) = dx/dt
-----
Et pareillement; dv/dt = lim(Δt -->0) [(v(t+Δt)-v(t))/ Δt]
Et si on veut écrire des équations différentielles représentant le phénomène étudié, c'est bien des dérivées qu'on doit manipuler et pas des valeurs moyennes.
-----
Sauf distraction.
2.Si les positions sont connues avec une incertitude x et qu'on peut négliger l'incertitude sur t, quelle incertitude v a-t-on sur la vitesse ?
Négligeant l'incertitude
t, l'incertitude v=x. J'ai tout juste ?Salut, je ne comprends pas comment exprimer dh/dt en fonction de v (q°3) .
Ni pourquoi : S(tuyau) = pi*d²/4 ?
Ces deux questions sont peut-être liées, je ne sais pas, mais merci beaucoup pour votre aide
J-P peux-tu me réexpliquer pourquoi dv/dt est constant ? je relis sans cesse ton raisonnement sans comprendre les articulations qui le régissent 
Merci d'avance pour ton attention.
dv/dt est constant ... parce que c'est le calcul qui le montre.
Si tu comprends comment on arrive à montrer que dv/dt = - g.d²/D², alors tout est dit ...
Puisque g = 9,8 m/s² est une constante (du moins dans le cadre du problème posé), D et d sont données, donc sont des constantes dans le problème posé.
-----
Mais j'ai quelques craintes que tes difficultés de compréhension se situent tout à la base, c'est à dire dans la maîtrise des notions de vitesse, d'accélération, de débit et autres...
Si c'est le cas, il faut revoir et comprendre parfaitement toutes ces notions avant d'essayer d'attaquer des problèmes concrets les utilisant.
Annuler
connectez vous