Inscription / Connexion Nouveau Sujet
Batman et la chute libre
Bonjour, j'aurais besoin d'aide pour cet exercice j'ai essayer de commence et je me demandais si vous pouviez me dire si je suis sur la bon chemin ?
Voici le sujet :
Pour pouvoir tester sa cape volante, Batman demande de l'aide a un théoricien physicien. Ils se rejoignent près d'une falaise pour pouvoir effectuer leur test :
Il saute de la falaise qui mesure 20 m de long
A une hauteur de 1000 m. Il y a un angle alpha de 1.5 °
1)En sautant de la falaise, combien de temps tcollision a Batman pour ouvrir la cape volante avant qu'il ne heurte le sol si la pente de la falaise est à l'angle alpha = 1.5°. On ne considère pas les frottements.
Pour cette question j'ai commencé par déterminer le système les forces et donc la 2ne loi de Newton
Somme des forces = ma
P=mg
On a donc a = g
On intègre et j'obtiens a la fin 1/2 gt^(2)+h0 et le reste je suis perdu...
Il faut chercher un tcollision en effectuantvune équation qui utilise le résultat de l'intégration précédente ? L'angle alpha me perturbe...
------
2) En supposant qu'une fois qu'il deploie sa cape volante, les forces de frottement
avec l'air et la force portante de l'air lui permet de planer le long d'une
trajectoire semi circulaire parfaite. Cette trajectoire va l'emmener d'une
chute verticale à un vol purement horizontale. La trajectoire a
un rayon qui vaut R = 100 m. Trouver le temps tailes pendant sa chute
verticale où il doit ouvrir ses ailes s'il veut arriver en position horizontale
à sa hauteur de vol libre hvol.
En tout cas merci de votre aide !
- Akkinda
Bonjour
Pourrais-tu recopier l'énoncé intégral ? Ce que tu as écris n'est pas très clair...
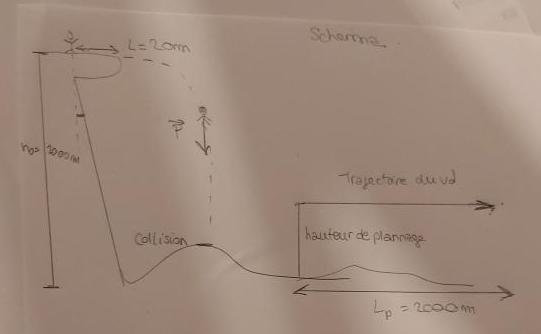
A ce que je comprends, la chute sans cape est verticale en absence de vitesse initiale indiquée, à partir d'un point situé 20m en surplomb de la falaise, un peu comme s'il se laissait tomber d'un plongeoir de 20m de long... Pas très réaliste du point de vue géologique...
La falaise n'étant pas verticale mais inclinée de 1,5°, le sauteur risque de rencontrer la falaise après une chute verticale de hauteur h :
La date de collision avec la falaise serait ainsi la durée d'une hauteur de chute de 764m... Je néglige l'épaisseur du plongeoir...
Tout cela n'est pas réaliste car, sur des hauteurs de chute aussi grandes, la vitesse devient très élevée et il n'est pas possible de négliger l'influence des frottements de l'air... Quant à la trajectoire en arc de cercle ensuite : elle défie les lois de la physique...
Si tu pouvais fournir un énoncé complet ainsi qu'un scan du schéma qui l'accompagne très probablement.
Tu es sûr que cet exercice n'est pas une plaisanterie ?
Bonjour,
Ce n'est pas une plaisanterie sinon je n'aurais pas demandé l'aide, mais je ne sais pas si j'ai le droit de donner le vrai énoncé :-/ je suis désolé j'essaye de changer un peu pour que ce ne sois pas obvious...mais c'est tout ce que j'ai. Vous avez bien résumé le début je vais essayer de vous donner un autre Schema.
1) En sautant directement de la plate-forme installée , combien de temps tcollision a Batman pour ouvrir sa cape volante agrémentée d'un moteur (pour effectuer la poussée si nécessaire avant de s'ecraser)
sur le flanc de la montagne, si la pente de la montagne est à un angle.
θ = 1.5° avec la verticale.
Nous ne considérons aucune résistance à l'air
pendant la chute libre.
Pour le schéma j'ai juste modifié la plateforme d'où il saute...Les questions concernant les frottements viennent à partie de la question 3
3) En supposant que la vitesse de Abbass a changée de Vailes à Vvol = 20 m/s en raison du frottement entre l'air et son corps, pendant sa trajectoire circulaire, estimez la valeur initiale, et finale de la force centripete
imposée sur le corps de Batman.
Fcentripete = mV 2 / R. Il pese (avec tout son
materiel du vol) m = 110 kg.
Selon votre avis, est-ce qu'un rayon de
notre ”rond point aerodynamique” R = 100 m est realiste si Batman souhaite survivre la trajectoire circulaire ? Expliquer votre réponse.
J'espere être assez clair merci.
-akkinda.
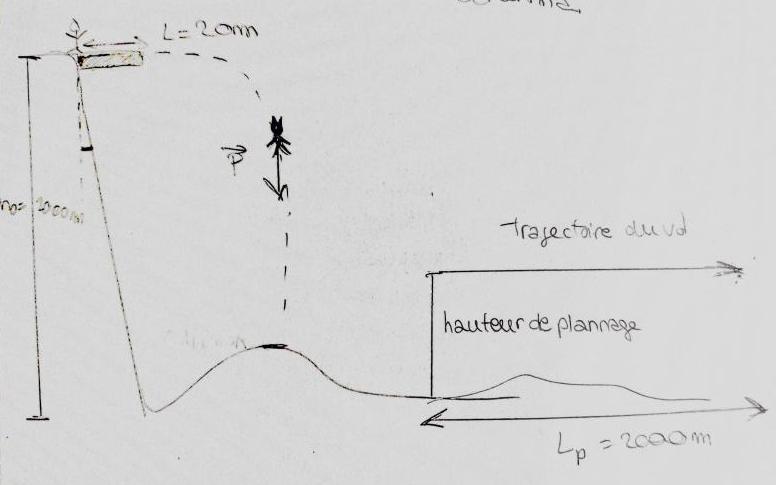
J'imagine plutôt batman se laisser tomber sans vitesse initiale du haut du plongeoir. Puisque la falaise n'est par verticale, il va heurter celle-ci après une chute de 764m comme expliqué précédemment.
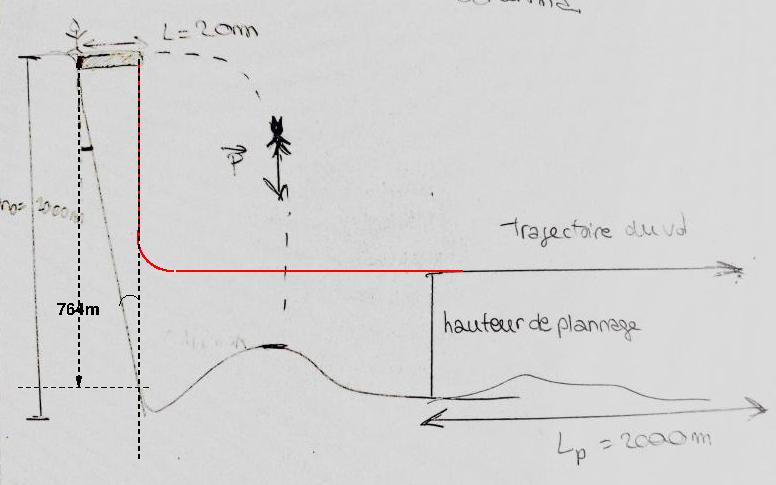
Pour éviter cela, il déploie sa cape, ce qui lui permet de décrire un arc de cercle d'un quart de cercle avant d'adopter une trajectoire horizontale. Sa trajectoire correspondrait donc au trait rouge du schéma modifié comme ci-dessous. Le schéma bien sûr, n'est pas à l'échelle...
Sous toute réserve...
C'est ca, car il faudra trouver par la suite le tcape ( qui déterminera à quel moment il doit ouvrir sa cape pour éviter Tcollision)
J'ai compris qu'il se laissait tomber aussi en chute libre.
Je me suis arrêté à 1/2g*t^2+ Cste
On trouve par la suite que Cste = h = 764 m
On cherche à quelle seconde il heurte le sol. Est-ce bon de faire une équation d'inconnue t?
En prenant un axe orienté vers le bas dont l'origine est à l'altitude de départ :
x=½.g.t2
S'il n'ouvre pas sa cape, il va s'écraser sur la falaise 764m plus bas. La date de colision est donc la valeur positive de t telle que x= 764m.
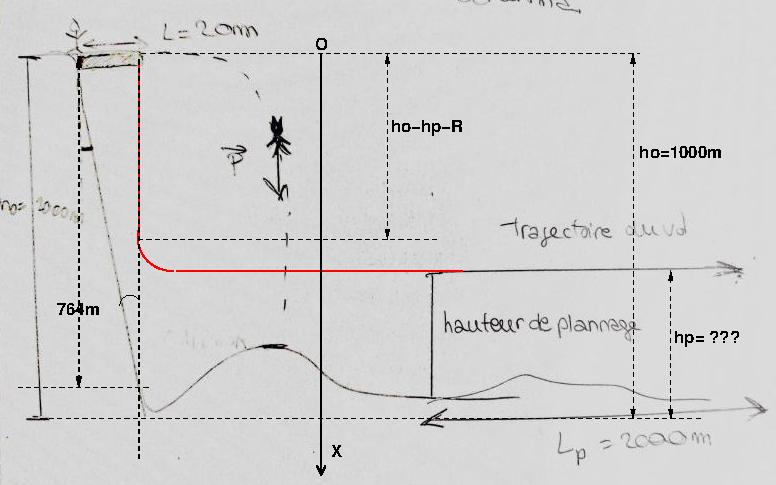
Je note hp la hauteur de planage dont la valeur numérique ne semble pas indiquée. comte tenu de la portion circulaire de trajectoire de rayon R, il doit ouvrir sa cape après une chute d'une hauteur x= (ho-hp-R). Facile d'obtenir la date correspondante....
La suite est l'étude du mouvement circulaire sur un quart de cercle....
Je te laisse réfléchir...
Merci pour votre Schema il est plus claire par rapport à ce qu'on a eut !
Du coup j'ai pu trouver Tcollision = 7s
Et pour le reste je pense savoir comment m'en sortir ! 
Merci !


