Bonjour pouvez m'aider s'il vous plaît merci



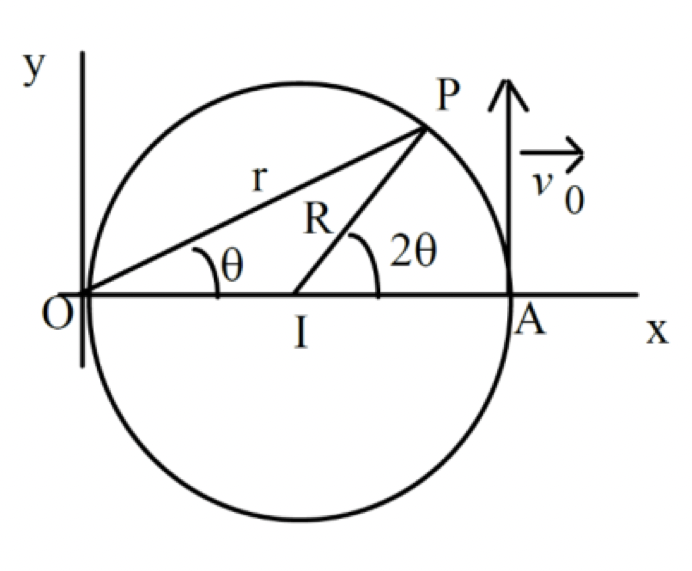
a. Représenter en P la base polaire de vecteurs unitaires 𝑢⃗ 𝑟 , 𝑢⃗ 𝜃 .
b. On désigne par r et 𝜃 les coordonnées polaires de la guêpe.
c. Définir l'équation polaire du cercle, r(𝜃).
d. Rappeler les expressions des vecteurs vitesse 𝑣 et accélération 𝑎 de la guêpe
dans cette base, puis calculer en fonction de 𝜃 et de ses dérivées successives par rapport au temps les composantes polaires radiales et orthoradiales des vecteurs position, vitesse et accélération de la guêpe.


pour la a) d'habitude on travaille avec r=R , j'ai du mal à démaré car pour moi l'équation du cercle elle dépend du rayon mais la r n'est plus le rayon du cercle...