Inscription / Connexion Nouveau Sujet
base cylindro-polaire
bonjour je demande de l'aide pour commencer cet exercice .
Dans le plan (xOy) d'un repère (O ;(ex) ⃗;(ey) ⃗;(ez) ⃗), le mouvement d'un point M est décrit par la variation de ses coordonnées cartésiennes en fonction du temps t
(x=-be^(-kt) cos(kt) et y=be^(-kt) sin(kt) Où b et k sont deux constantes positives
1)a) Déterminer en fonction de t les coordonnées polaire p=(OM) ⃗ et θ=kt du point M.
b) En déduire l'équation polaire de la trajectoire du point M.
2)a)déterminer en fonction du temps t les composantes polaire du vecteur vitesse.
b) En déduire l'angle 
=(om,v)
c)en déduire la nature du mouvement
3a)Déterminer en fonction du temps t les composantes polaires du vecteur accélération
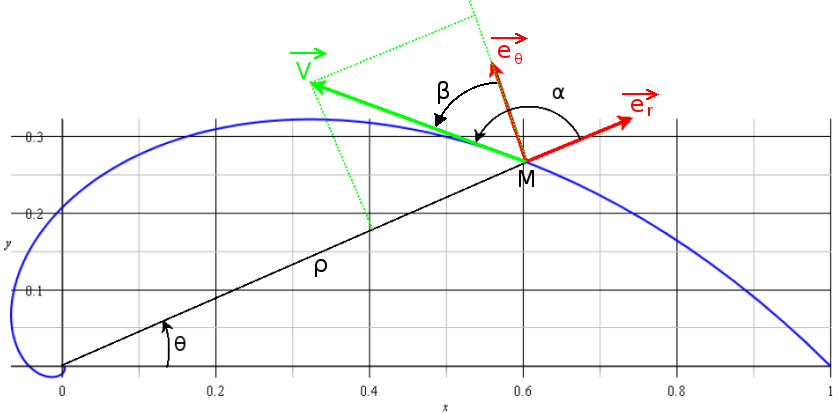
b)préciser la direction du vecteur accélération et représenter les vecteurs vitesse et accélération sur une figure
4)déterminer en fonction de t les composantes tangentielles et normale du vecteur accélération
Bonjour
Les coordonnées cartésiennes de M se déduisent des coordonnées polaires par les relations :
Ici, on peut procéder par simple identification. Je t'indique tout de même la méthode générale permettant d'obtenir les coordonnées polaires en fonction des coordonnées cartésiennes :
avec du signe de x et
du signe de y.
Je te laisse réfléchir et proposer une solution.
Mon message du 21-10-18 à 15:11 est toujours valide pour un mouvement d'un point matériel dans un plan.
alors pour p j'ai trouvé be-w et j'ai trouvé tan(-w)
est ce juste ?
si oui comment fais ton l'équation alors ? parce que j'en ai jamais entendu parler
Tu y es presque mais il y a une difficulté due au signe « - » dans l'expression de x. Si on procède par simple identification, on obtient, en supposant b > 0 (
ne peut pas être négatif par convention) :
Dessine un cercle trigonométrique si cela peut t'aider : on obtient :
Il faut être clair au niveau des notations. Comme le plus souvent en mécanique, je note 
l'angle polaire soit l'angle ; il y a une maladresse dans ton énoncé ; il serait préférable de poser :
, sauf bien sûr si tu as commis une faute de frappe en ajoutant un signe « - » dans l'expression de x, les choses deviendraient alors très simples...
Une simple substitution :
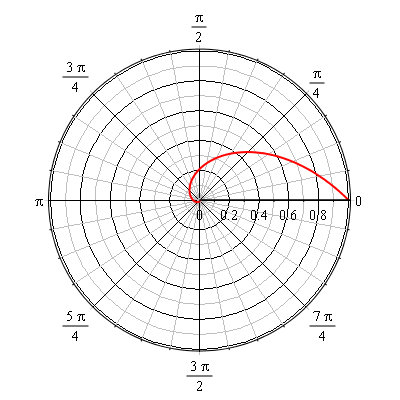
Il s'agit d'une spirale exponentielle. Voici un exemple correspondant à b=1m tracée entre =0 et =2
rad
pour me mettre les idées clairs
qu'est ce que l'on nous demande vraiment par équation polaire? c'est l'equation de la trajectoire?
L'équation polaire de la trajectoire est l'équation : = f().
Les équations qui sont fournies par l'énoncé sont les équations paramétriques de la trajectoire.
Pour avoir une trajectoire avec plusieurs "tours" autour du centre O, il aurait fallu poser comme équations paramétriques :
L'équation polaire devenant, en posant toujours : :
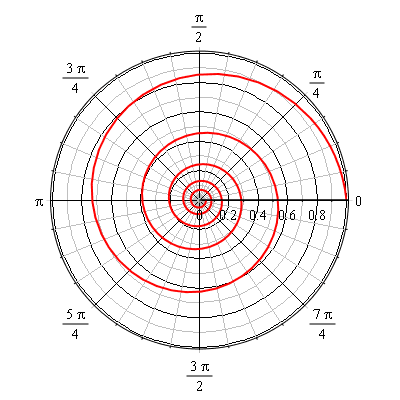
Voici le résultat obtenu pour b=1m, k=10rad, variant de 0 à 10rad.
Bonsoir
d accord je comprend mieux
j'ai essayé de continué l'exercice hier pour déterminer les composantes polaires de la vitesse il m'a suffit de dérivé l'équation polaire.
mais alors comment trouver ensuite l'angle former par le vecteur om et le vecteur vitesse?
avec : et
Pour l'angle : fait une figure propre en représentant les deux composantes du vecteur vitesse ainsi que la résultante de ces deux composantes. Un minimum de trigonométrie te donne alors le résultat... Trace aussi la trajectoire pour vérifier la cohérence du résultat.
Bonjour vanoise
désolé du retard j'étais en examen toute la semaine
sinon il ya pas une manière théorique de la calculé plutôt que graphiquement?
sinon il ya pas une manière théorique de la calculé plutôt que graphiquement?
Bien sûr que si !
je t'ai indiqué la méthode dans mon message du 22-10-18 à 22:28. Tu exprimes les composantes du vecteur vitesse suivant er et e
. La figure précédente permet d'arriver ensuite à :
Annuler
connectez vous