Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

Balistique: Tirs parabolique et plongeant. Dénivellation?

Posté par
Leucippe 25-07-19 à 12:13

Bonjour,

J'essaie de résoudre (pour moi) des équations de balistique:
on veut atteindre un point avec une dénivellation de -y.

On estime que la norme de la vitesse initiale, V0, est connue. L'angle initial, alpha0 aussi.

-Seulement, j'aimerais trouver le tir plongeant qui puisse atteindre ce même point, sans passer par un sommet de parabole.
J'aimerais donc trouver l'angle Beta0 du tir plongeant, en fonction du premier tir (c'est-à-dire de son alpha0).
En ayant la même norme de vitesse.
Tout cela en ayant conscience que les temps auront certainement une différence, qui se répercuterait sur le x et sur les y, mais pas au même taux.


J'ai fait un dessins, ai rédigé des systèmes d'équations dont j'ai ensuite essayé de résoudre celles-ci, jusqu'ici sans succès, sachant qu'en les combinant, certainement de manière peu méthodique parfois, il a pu m'arriver d'obtenir des raisonnements circulaires je crois - quoique l'apparence assez compliquée de certaines équations pouvait laisser croire le contraire.

-Dans tout ça, ce que je en comprends pas:
À norme de vitesse initiale donnée, pour le tir en parabole, je n'arrive pas à comprendre si je peux fixer la dénivellation y, et essayer de rétrograder pour trouver l'angle du tir plongeant (j'ai un doute que ce soit faisable, au sens où les vitesses au point de la dénivellation comme en l'origine, ne sont pas les mêmes entre elles).

Géométriquement:
-le tir en parabole (vers en-dessus) me donne les trois points: S du sommet, A horizontal, et j'ai même pu trouve l'abscisse correspondant à l'ordonnée (-y) et constater sa différence d'avec l'abscisse de A, (qui apparaît de ma nièce explicite);
-le tir direct (plongeant), n'ayant pas de sommet sur la trajectoire du tir, fait que je n'ai que 2 point dessus (origine et rencontre avec dénivellation). Or on sait très bien que - géométriquement - une courbe ayant une dérivée-2ème uniquement négative (concave), ne saurait être définie par 2 points; il en faudrait au moins 3. Donc j'en obtient potentiellement des possibilités continûment indénombrables, si je ne connais la vitesse (alors que j'en connais la norme).

Je devrait peut-être fixer le temps commun pour une vraie rencontre, simultanée, des 2 courbes, ce qui, avec la norme de vitesse et avec angle positif, pourrait me donner un (-y) cohérent avec l'angle négatif recherché.
-Seulement, cela fait 3 jours que je planche sur ce problème: 1er jour, manuscrit; 2ème jour, rédaction des équations sur Word, pour y voir plus clair, et depuis, exploitation additionnelle de Excel pour stocker tous les intermédiaires de calcul, puis retour, sur Word, pour rédiger mes équations numériques avec dimensions, afin de vérifier qu'il n'y a pas d'incohérence, ni entre mes chiffres, ni en termes de dimensions, ce que je vais encore essayer en attendant votre aide, que j'espère.
Dans ce message, je vais essayer de vous fournir un tableau issu de mes résultat Excel, en plus des formules Latex.

Mes principaux calculs:
a: \begin{cases} & \text a_x = 0 \\ & \text a_y = -g \end{cases} \\ V(t): \begin{cases} & \text V_x(t) = V_x = V \cdot \cos \left( \alpha _0 \right) \\ & \text V_y(t) = -g\cdot t+V\cdot \sin \left( \alpha _0 \right) \end{cases} \\ R(t): \begin{cases} & \text x(t) = V_x\cdot t = V \cdot \cos \left( \alpha _0 \right)\cdot t \\ & \text y(t) = -\frac{1}{2}g\cdot t+V\cdot \sin \left( \alpha _0 \right)\cdot t \end{cases} \\ t_y_S = \left(V\cdot \sin \left(\alpha_0 \right) \right)/g \\ S\left(\frac{V^2}{2\cdot g}\cdot \sin \left(2\cdot \alpha_0 \right); \frac{V^2}{2\cdot g}\left[\sin \left(\alpha_0 \right) \right]^2 \right) \\ t_A = 2\cdot t_y_S \\ A\left(\frac{V^2}{g}\cdot \sin \left(2\cdot \alpha_0 \right); 0 \right) \\

-Puis, je reprends les équations de vitesse, mais pour le point B, à trouver, sur la dénivellation; j'essaie de résoudre son équation en y, avec une dénivellation (-y); il s'agit donc de résoudre une équation à 2 temps possibles, l'un étant avant le tir, je ne le prends pas en compte; je considère le temps positif; en voici l'expression la plus simple:

t_B_+ = t_S + \sqrt{\left(t_S \right)^2+\frac{2\cdot y}{g}}

que je multiplie par la vitesse horizontale, pour obtenir abscisse de B:
x_B_+ = V\cdot\cos \left( \alpha _0 \right)\cdot t_B
qui avec la multiplication de sinus par cosinus du même angles, donne le sinus de l'angle doublé:
B = \left(\frac{V^2}{g}\cdot \sin \left(2\cdot \alpha_0 \right)+V\cdot \cos\left(\alpha_0 \right)\cdot \sqrt{\left(\frac{V\cdot \sin \left(\alpha_0 \right)}{g} \right)^2+\frac{2\cdot y}{g}} ; -y \right)

-J'essaie aussi de prendre l'équation des y en général, et d'y introduire - à la place du temps "t", l'expression x sur Vx, (cette vitesse-ci étant constante), ce qui me donne comme équation du 2nd degº (mais je n'arrive pas à savoir si je dois ré-inclure la constante -y (ici en positive):
y_x_B = -\frac{1}{2}\cdot g\cdot \left[\frac{x}{V\cdot \cos \left(\alpha_0 \right)} \right]^2+V\cdot \sin \left(\alpha_0 \right)\cdot \frac{x}{V\cdot \cos \left(\alpha_0 \right)}

-avec la dénivellation yB = -y, mise du même côté:
0 = -\frac{1}{2}\cdot g\cdot \left[\frac{x_B}{V\cdot \cos \left(\alpha_0 \right)} \right]^2+V\cdot \sin \left(\alpha_0 \right)\cdot \frac{x_B}{V\cdot \cos \left(\alpha_0 \right)}+y

-sachant de plus que sinus au carré plus cosinus du même angle, au carré, font 1:
\left[-\frac{1}{2}\cdot g\cdot \left(\frac{x_B}{V} \right)^2 \right]\cdot \left[\tan \left(\alpha_0 \right) \right]^2+x_B\cdot \tan \left(\alpha_0 \right)-\frac{1}{2}\cdot g\cdot \left(\frac{x_B}{V} \right)^2 = y_B

-Si yB est constant, je le ramène donc du bon côté (je fais aussi une emphase, avec V0, pour bien montrer que c'est la vitesse initiale:
\left[-\frac{1}{2}\cdot g\cdot \left(\frac{x_B}{V_0} \right)^2 \right]\cdot \left[\tan \left(\alpha_0 \right) \right]^2+x_B\cdot \tan \left(\alpha_0 \right)-\frac{1}{2}\cdot g\cdot \left(\frac{x_B}{V_0} \right)^2 - y_B = 0

-donc le déterminant vaut alors:
\Delta := \left(x_B \right)^2-4\cdot \left[-\frac{1}{2}\cdot g\cdot \left(\frac{x_B}{V_0} \right)^2 \right]\cdot \left\{-\left[\frac{1}{2}\cdot g\cdot\left(\frac{x_B}{V_0} \right)^2 +y_B \right] \right\}
,du coup, la tangente de l'angle, en prenant la version avec "plus racine du delta":
\Delta := \left(x_B \right)^2-4\cdot \left[-\frac{1}{2}\cdot g\cdot \left(\frac{x_B}{V_0} \right)^2 \right]\cdot \left\{-\left[\frac{1}{2}\cdot g\cdot\left(\frac{x_B}{V_0} \right)^2 +y_B \right] \right\} \\ \tan \left(\alpha_0 \right)_- = \frac{x_B-\sqrt{\left(x_B \right)^2-4\cdot \left[\frac{1}{2}\cdot g\cdot \left(\frac{x_B}{V_0} \right)^2 \right]\cdot \left\{\left[\frac{1}{2}\cdot g\cdot\left(\frac{x_B}{V_0} \right)^2 +y_B \right] \right\}}}{2\cdot g\cdot\left(\frac{x_B}{V_0} \right)^2 }

-j'avoue que je ne m'en sors plus, car l'analyse numérique ne correspond à rien... si ce n'est peut-être à l'angle en B.

Je ne sais plus où j'en suis, et n'arrive pas à retrouver l'autre possible angle de départ; j'ai besoin d'aide.

-J'essaie de fournir mes résultat intermédiaire issu de Excel, si ça peut aider:

DonnéeValeur
g9,81 m/s2
3,14159265358979
Angle_1er tir\frac{\pi }{3}
V73 m/s
yB-y
tS6,44442961022059 s
tA12,8888592204412 s
xB/V09,666644415330890 s


N. B.:
-je me suis inspiré de
fr.wikipedia.org/wiki/Trajectoire_parabolique
fr.wikipedia.org/wiki/Portée_(balistique)
la 1ère des 2 sources m'ayant aidé pour une équation en tangente d'angle. Je sens que j'approche, mais plus je m'approche de la solution, moins de comprends, d'où difficulté vis-à-vis de la cohérence.

-En vous remerciant d'avance infiniment pour votre aide que j'attends avec impatience, je vous souhaite une bonne matinée.

P. S.:
Le dessin joint a été inséré avec une angle de 90º (à gauche), je n'ai pas compris pourquoi.

Balistique: Tirs parabolique et plongeant. Dénivellation?

Posté par
vanoisere : Balistique: Tirs parabolique et plongeant. Dénivellation? 25-07-19 à 14:31

Bonjour
Avec les notations classiques en choisissant comme point de départ l'origine du repère, l'équation de la trajectoire est :

y=-\dfrac{g}{2.V_{o}^{2}.\cos^{2}\left(\alpha\right)}x^{2}+V_{o}\cdot\tan\left(\alpha\right)\cdot x=-\dfrac{g\left(1+\tan^{2}\left(\alpha\right)\right)}{2.V_{o}^{2}}x^{2}+V_{o}\cdot\tan\left(\alpha\right)\cdot x

On veut que cette trajectoire contienne le point B(L,-h) avec L et h deux constantes positives.Ce qui conduit à :

-\dfrac{g\left(1+\tan^{2}\left(\alpha\right)\right)}{2.V_{o}^{2}}L^{2}+V_{o}\cdot\tan\left(\alpha\right)\cdot L+h=0

Tu obtiens une équation du second degré d'inconnue tan(). Si la vitesse initiale Vo est suffisante, cette équation admet deux solutions ; une solution positive qui correspond à la trajectoire “en cloche”, une solution négative qui est celle qui t'intéresse.

Posté par
Leucippere : Balistique: Tirs parabolique et plongeant. Dénivellation? 25-07-19 à 17:17

Merci Vanoise pour votre réponse!

Je vais essayer d'appliquer les nombres à vos réponses, dont je vous remercie; toutefois, il me reste un doute, à cause d'une analyse dimensionnelle simple:
-\frac{9,81\left[\frac{m}{s^2} \right]\cdot \left(1+\left[\tan \left(\alpha_0 \right)\right]^2 \right)}{2\cdot \left(V_0 \right)^2\left[\frac{m^2}{s^2} \right]}\cdot L^2\left[m^2 \right]+V_0\left[\frac{m}{s} \right]\cdot \tan \left(\alpha_0 \right)\cdot L\left[m \right]+h\left[m \right]=0 \\ \Rightarrow \frac{\frac{m}{s^2}}{\frac{m^2}{s^2}}\cdot m^2+\frac{m^2}{s}+m=m+\frac{m^2}{s}+m\neq m

Posté par
vanoisere : Balistique: Tirs parabolique et plongeant. Dénivellation? 25-07-19 à 17:35

Tu as raison : en recopiant la formule dans l'éditeur d'équations, j'ai laisser traîner un Vo en trop. Je rectifie :

y=-\dfrac{g}{2.V_{o}^{2}.\cos^{2}\left(\alpha\right)}x^{2}+\tan\left(\alpha\right)\cdot x=-\dfrac{g\left(1+\tan^{2}\left(\alpha\right)\right)}{2.V_{o}^{2}}x^{2}+\tan\left(\alpha\right)\cdot x

-\dfrac{g\left(1+\tan^{2}\left(\alpha\right)\right)}{2.V_{o}^{2}}L^{2}+\tan\left(\alpha\right)\cdot L+h=0

Posté par
Leucippere : Balistique: Tirs parabolique et plongeant. Dénivellation? 25-07-19 à 21:45

Merci beaucoup.

Je vais encore essayer pour l'application numérique.

À première vue, les valeurs numériques (norme de vitesse, et dénivellation) ont une influence énorme, car certaines valeurs peuvent vite dépasser ce qui est accepté par Excel (qui propose plusieurs décimales de plus que la calculatrice, pour Pi).

Posté par
vanoisere : Balistique: Tirs parabolique et plongeant. Dénivellation? 25-07-19 à 23:50

Tu ne précises pas les coordonnées de ton point B. Attention :bien sûr ici, les frottements de l'air sont négligés...
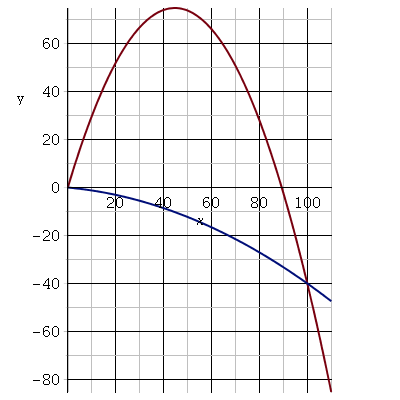
Il est exact que l'équation que je t'ai fournie n'admet deux solutions de signes différents que pour certaines valeurs numériques. Voici un exemple :
L=100m ; h= 40m ; Vo=40m/s ;
les deux valeurs de tan() sont : 3,353 et -0,0909. Voici les deux trajectoires correspondantes.

Balistique: Tirs parabolique et plongeant. Dénivellation?

Posté par
Leucippere : Balistique: Tirs parabolique et plongeant. Dénivellation? 26-07-19 à 11:03

Merci bien, mais vous venez de fournir les 2 coordonnée du point B, avec L et h ?

(D'ailleurs, je ne vois pas comment on peut s'en passer; la seule autre possibilité que je vois, serait de fixer un temps commun - ce qui mènerait (évidemment) à alpha0 = 0, qui serait un tir à raz de l'horizontale).

Ce qui m'intéresse le plus, c'est de savoir avec quel outil je puis visualiser ces trajectoires, s'il vous plaît? (Celui que vous avez utilisé).

J'ai essayé avec Excel, mais Excel ne "comprends" pas, c'est clair, que la trajectoire (du haut) subit une accélération à la 2ème puissance de t; il ne peut pas savoir que c'est du 2ème ordre.

J'ai crû qu'il allait donner ça en 1ère approche avec un minimum de points (trois), mais il a l'air de partir du principe opposé, qu'il s'agît d'une courbe au plus haut degré possible avec semble-t-il une condition d'avoir la concave entre 2 points - mais pas au-delà).

Posté par
vanoisere : Balistique: Tirs parabolique et plongeant. Dénivellation? 26-07-19 à 12:00

Une fois fixées L , h et Vo, je détermine les deux racines de l'équation du second degré avec tan() comme inconnue. Tu as alors les équations des deux trajectoires. Les deux paraboles peuvent alors être tracées avec un tableur.
Pour réaliser un tir, il faut  connaître les coordonnées de la cible et la vitesse initiale du projectile. Reste alors à ajuster l'angle...

Posté par
Leucippere : Balistique: Tirs parabolique et plongeant. Dénivellation? 26-07-19 à 15:22

Bonjour,

je crains de commencer à vous faire perdre patience.

Puis connaître le nom de votre tableur? -Avec Excel, que j'utilise actuellement, c'est déjà prise de chou pour faire un basique graphique ortho-normé.

Je ne sais pas comment établir une courbe. De mon point de vue, il faut établir une suite de x à la précision 10^(-15), puis donner à chaque fois l'équation dessus comme valeur retournée. Mais ça risque de faire un peu trop de valeurs...

-Pourrais-je vous demander étape-par-étape entre l'établissement de 2 ou 3 x, et l'établissement graphique de la courbe, s'il vous plaît?

Posté par
vanoisere : Balistique: Tirs parabolique et plongeant. Dénivellation? 26-07-19 à 15:56

Première ligne : destinées aux noms des colonnes :
a1 : entrer x(m) ; b1 : entrer y1(m) ordonnée pour la première valeur de la tangente ; c1 : entrer y2(m), ordonnée pour la seconde valeur de la tangente.
Deuxième ligne : entrer les valeurs initiales : 0 en a2, en b2 et en c2.
Troisième ligne : en a3 entrer la formule qui, par copie vers le bas, entrera les valeur 1,2,3... jusqu'à 100 : =a2+1
en b3 : entrer la formule (commencer par =) donnant y1 en tapant a3 à la place de x
en c3 : entrer la formule donnant y2 en remplaçant x par a3.
Ensuite :
sélectionner les cases de la ligne n° 3. placer le pointeur de la souris sur la "poignée" en bas à droite de l'ensemble sélectionner. Tout en appuyant sur le bouton gauche de la souris en permanence, "tirer" le pointeur vers le bas jusqu'à la ligne 110.
Le calcul s'effectue alors automatiquement ; il ne te reste plus qu'à faire apparaître les deux courbes...

Posté par
Leucippere : Balistique: Tirs parabolique et plongeant. Dénivellation? 26-07-19 à 19:09

Donc pour le principe, il me semble que j'avais deviné: je suis obligé de faire des tests d'approche pour des x incrémentés (mais de 1). Dû à une raison inconnue, j'ai une "aiguille" en négatif au début du graphique; un point de discontinuité.

-Mais quelle est la différence entre y2 et y1, je vous prie?

Car vous mentionnez d'entrer la formule (je comprends: celle de la tangente), où y1 est a3 à la place de x,
puis mentionnez que y2 est x remplacé par a3, ...ce qui du point de vue logique revient exactement au même.

Balistique: Tirs parabolique et plongeant. Dénivellation?

Posté par
Leucippere : Balistique: Tirs parabolique et plongeant. Dénivellation? 26-07-19 à 22:21

Chère Vanoise,

Quelque chose me dit que nous sommes proches du résultat!

-Par ce que le philosophe Miles Mathis appelle des tiny corrections (termes souvent utilisés de manière péjorative pour mettre en évidences les incohérences des théories du mainstream, ceci dit), j'ai l'impression que j'approche à grand pas de ce qui m'est requis...

-D'expérience, je sais dans l'application numérique que je dois manier finement la relation entre d'une part -y, et x/V0 d'autre part... à cause de la racine.

Bien évidemment, au stade où j'en étais, je ne pouvais pas me payer le luxe d'une application trop "générale"; j'ai donc essayé avec des valeurs on-ne-peut-plus particulières (excepté l'angle positif initial, que je n'ai quand-même pas mis à /4, mais à /3, qui reste quand-même assez "repérable"); j'ai aussi fixé V0 à 1m/s, et y à 1m.

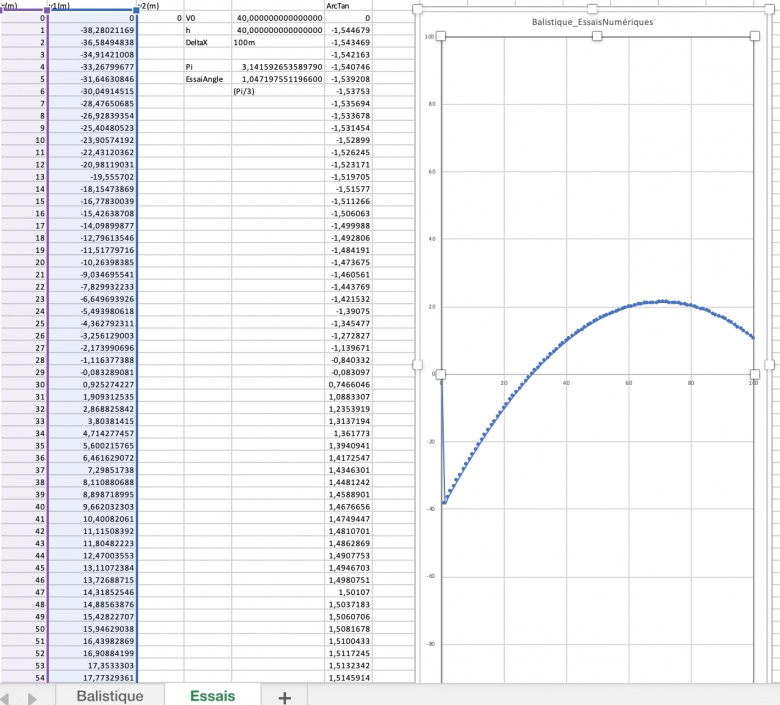
Et... j'obtiens graphiquement un résultat plutôt intéressant (ci-joint).

Je reconnais que j'avais commis l'erreur basique d'oublier une priorité d'opération (multiplier, diviser, puis multiplier - au lieu de multiplier 2 fois, puis seulement ensuite diviser).

Surtout, j'ai pensé à re-remplacer mon sin(2*Alpha)/2, par de nouveau sin(alpha)*cos(alpha), car sinon, la première version donne hors de notre cadre pour les angles supérieurs à 45º, ...évidemment.

Bref, nous nous approchons de la solution.

Pour moi, le décryptage des imbrications devrait pouvoir ne prendre plus que quelques jours (1, j'espère) voire une semaine.

Mais je vais essayer de vous laisser un peu plus tranquille; loin de moi l'envie de faire l'égocentrique. Mes demandes d'excuses, si j'ai donné l'impression inverse.

N. B.:
-Le graphique n'a plus mon ancienne apparence de courbes concaves seulement entre points.
Le fait que sa 2ème dérivée est exclusivement négative est visible sur mon graphique (joint, donc), et ce qui n'est pas dû au dé-zoomage. Mon graphique, malgré l'apparence - il est vrai - étrange des échelons (répartition), est ortho-normé.
-L'affichage de la courbe plongeante reste pour moi un mystère (je pense que c'était ça, vote y2... mais comment le calculer-représenter, et si je n'ai que deux points véritables de repère), mais l'atteinte de résultats cohérents hors affichages exhaustifs, sera pour moi satisfaisante.

Rappel de mes valeurs:
V0 = 1m/s;
y = -1 m.

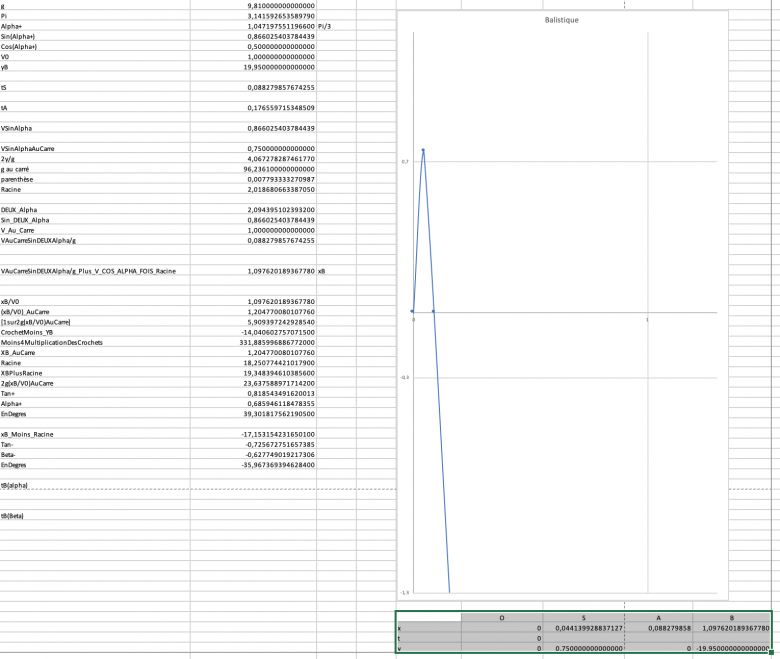
Balistique: Tirs parabolique et plongeant. Dénivellation?

Posté par
vanoisere : Balistique: Tirs parabolique et plongeant. Dénivellation? 26-07-19 à 22:47

C'est quoi cette colonne “ArcTan” ? La tangente se calcule à part comme déjà expliqué. Avec les valeurs numériques choisies arbitrairement, la tangente a deux valeurs possibles : 3,353 et -0,0909 ; la colonne y1 correspond à la première valeur (parabole tracée en rouge), la seconde valeur correspond à la colonne y2. Pour être encore plus clair, la formule à taper dans la cellule b3 est :

-9.81*(1+3.353^2)*a3^2/3200+3.353*a3

Pour la cellule c3 : remplacer 3,353 par -0,0909.

Posté par
Leucippere : Balistique: Tirs parabolique et plongeant. Dénivellation? 27-07-19 à 07:40

Je pense que vous parlez de mon graphique de 2 de mes messages avant.

-La colonne ArcTan était supposée être une vérification - sauf que j'étais fatigué, empêtré, et que j'ai appliqué ça à [y] car j'étais dans les nuages. Quant à l'aiguille du début, c'est parce qu'on est passé de 0 à quelque chose. Sauf que ma courbe a débuté en négatif.

Votre 3ème phrase est une contradiction en soi.
Pour info, j'ai corrigé la proposition 3 de Zénon d'Élée pour notre implication dans le cas où soi-disant "Faux mène à vrai" (mais on va presque y arriver) - chose qui est passée inaperçue pendant plus de 2'400 ans aux yeux des plus grands intellectuels, pire: ils ont accepté l'implication courante, anti-temporelle, avec "Faux mène à vrai", qu'aucune domaine un tant soi peu scientifique n'utilise, et pour ceux qui le sont moins, ils ont dû appliquer des transformations sophistiquées pour éventuellement la rendre temporelle.

J'ai retourné l'exemple de Zénon contre lui-même, en montrant dans "car de la Terre vole [est faux], il ne s'ensuit pas que la Terre existe"; le verbe exister n'opère aucunement la Terre, qu'il laisse égale à elle-même, la Terre (tout court), tant et si bien que c'est elle, vraie, qui est utilisée dans La Terre vole (est faux). Résultat: Vrai mène à faux... comme dans l'expérience tous les jours.

Ma logique est temporelle de manière native...

Donc inutile d'essayer d'être condescendant avec moi.

-Votre 3ème phrase est une contradiction: "Avec des valeurs numériques choisies arbitrairement, la tangente a 2 valeurs possibles".

-Avec des valeurs numériques choisies, fixées, les valeurs pour la tenante ne sont pas des valeurs "possibles"; ce sont des valeurs fixées, et cela ne m'intéresse pas.

Pire, vos angles ne correspondent à rien de spécial; environ 73,39º pour le positif. Quand on a quelqu'un dans la mouise, on commence pas par lui donner du quelconque; on lui donne du particulier: du repérable. Ce que je fais à mon endroit.
Ou alors, vous ne connaissez pas la méthode scientifique.

Et comme déjà expliqué...

-Je ne veux pas savoir que alpha vaut "3,353".

Prémisse principale:
-Je veux trouver une dénivellation en fonction du alpha-positif;
Prémisse secondaire:
-je veux trouver une abscisse commune à un alpha-négatif pour cette dénivellation.
Conclusion:
Je veux obtenir alpha-négatif en fonction de alpha-positif!


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !