Inscription / Connexion Nouveau Sujet
Balistique inverse
Bonjour à tous,
J'ai un problème en physique que je n'arrive pas à résoudre.
On considère un système soumis à la force de gravité et aux frottements. On aimerait étudier sa trajectoire dans un repère (Oxy). On ne connait cependant pas la vitesse initiale ainsi que l'angle initial avec lequel le système a été projeté. Les données sont les suivantes :
- le coefficient de pénétration dans l'air de ce système
- la masse du système
- la vitesse finale (d'impact) du système
- l'angle d'impact du système
- les coordonnées (en x et pas en y) du point d'impact (là où le système a finit sa course) et du point de départ (là où le système a été projeté)
En écrivant les équations du mouvement et en résolvant l'équation différentiel, je me suis retrouvé avec les deux inconnues (vitesse et angle initial) et la variable t (temps). Je ne vois pas comment les trouver.
Est-ce que quelqu'un aurait une idée ?
Un des moyens de faire, puisqu'on a deux variables inconnues, serait d'étudier le problème si on faisait varier une de ces deux variables. Ce qui veut dire écrire des équations différentielles partielles, mais je ne sais pas comment les écrire...
Merci d'avance pour votre réponse ! 
Sans y avoir beaucoup réfléchi (et donc à vérifier) :
dVx/dt = -k/m .Vx² (avec k = 1/2.Rho(air) * Cx * S)
dVy/dt = -g - k/m .Vy² (sur la partie ascendante de la trajectoire)
et
dVy/dt = -g + k/m .Vy² (sur la partie descendante de la trajectoire)
Avec Vx(0) = Vo.cos(alpha) et Vy(0) = Vo.sin(alpha)
On devrait pouvoir trouver Vx(t) et Vy(t) en fonction de Vo, k(connu) et alpha. (et donc aussi V(t) = RC(Vx² + Vy²) et l'angle de la tangente à la trajectoire)
Et en intégrant, trouver x(t) et y(t) en fonction de Vo, k(connu) et de alpha
...
Sauf distraction (ou erreur). 
Tout d'abord, merci pour votre réponse 
Je me suis (sûrement) mal exprimé. Ma question est de savoir s'il on peut trouver la vitesse initiale et l'angle initiale (numériquement) s'il on connait toutes les données précitées ?
Il me semble que oui.
Après avoir résolu toutes les équations différentielles, on a :
vx en fonction de t, Vo, alpha et k(qui est connu)
vy en fonction de t, Vo, alpha et k(qui est connu)
|v| en fonction de t, Vo, alpha et k(qui est connu)
x en fonction de t, Vo, alpha et k(qui est connu)
y en fonction de t, Vo, alpha et k(qui est connu)
angle de la tangente à la trajectoire en fonction de t, Vo, alpha et k(qui est connu)
On a donc 6 relations avec 3 inconnues (Vo , alpha et t), c'est plus quassez.
Par exemple (mais je ne l'ai pas fait)
Dans la relation donnant angle de la tangente à la trajectoire en fonction de t, Vo, alpha et k(qui est connu), on entre la valeur de l'angle d'impact
... on a donc une première équation liant (Vo , alpha et t)
Dans la relation donnant v(t) en fonction de t, Vo, alpha et k(qui est connu), on entre la vitesse d'imact.
... on a donc une deuxième équation liant (Vo , alpha et t)
Dans la relation donnant x en fonction de t, Vo, alpha et k(qui est connu), on entre la coordonnée en X du point d'impact.
... on a donc une 3ème équation liant (Vo , alpha et t)
On résout ce système de 3 équations à 3 inconnues ... et on obtient donc les valeurs de alpha, de Vo et de t(durée du tir).
Pas vérifié. 
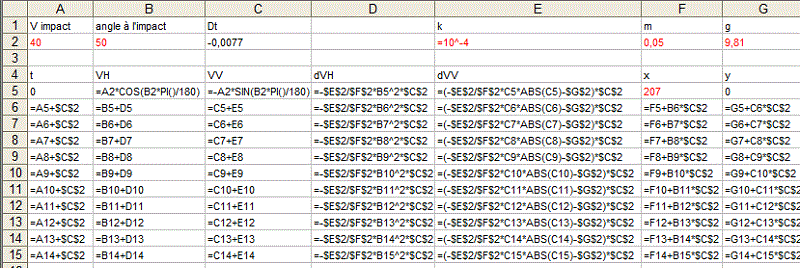
On peut aussi confier le calcul à un tableur, Excel par exemple.
Voici une copie écran des premières lignes de ce fichier (il y a 1000 lignes tirées vers le bas)
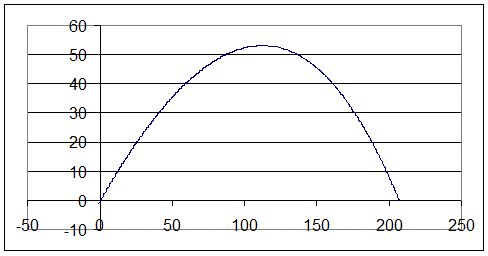
Le graphe de y = f(x) obtenu est le suivant :
On entre dans les cases en rouge, la vitesse à l'impact, l'angle (en °) à l'impact, l'abscisse du point d'impact, les valeurs de k, de m et de g
On entre, par essais successif, la valeur de Dt, pour que la courbe passe par l'origine (supposée être l'origine du tir).
On peut aller lire dans les cellules du bas, VH(0rigine) ; Vv(0rigine); en déduire l'angle de tir ...
Sauf distraction.

Merci pour cette indication et de votre temps accordé à ma question !
Je vais essayer ça aujourd'hui 
Bonjour
En écrivant les équations du mouvement et en résolvant l'équation différentiel
S'il s'agit de traiter le problème numériquement, une simple simulation informatique suffit effectivement. Dans ce cas, oublie mon message.
S'il s'agit de traiter le problème de façon littérale pour plus de généralité, les choses sont beaucoup plus compliquées. Il faut une bonne maîtrise de la fonction "tangente hyperbolique" ou au moins une bonne maîtrise des exponentielles... S'il s'agit bien de l'objectif de l'exercice : poste ici les expressions de Vx, Vy, x et y en fonction du temps que tu as obtenues.
L'approche théorique (établissement des équations différentielles) a été faite dans mon premier message.
dVx/dt = -k/m .Vx² (avec k = 1/2.Rho(air) * Cx * S)
dVy/dt = -g - k/m .Vy² (sur la partie ascendante de la trajectoire)
et
dVy/dt = -g + k/m .Vy² (sur la partie descendante de la trajectoire)
Sauf erreur, cela donne :
Avec t = 0 à l'instant de l'impact (et donc pour t <= 0)
Vx(t) = 1/(k/m * t + C3)
Vy(t) = -racine(mg/k) * tanh(racine(k.g/m) * (C1 + t)) pour la partie descendante de la trajectoire. (1)
Vy(t) = -racine(mg/k) * tan(racine(k.g/m) * (C2 + t)) pour la partie ascendante de la trajectoire. (2)
On détermine C3 par Vx(0) = Vimpact * cos(angle impact)
On détermine C1 par Vy(0) = Vimpact * sin(angle impact)
On passe de (1) à (2) en t = -C1 (Vy = 0) et donc C2 = C1
On détermine x(t) et y(t) en intégrant les expressions de vx(t) et de vy(t), ce qui est sans difficulté.
Si on remet dans ces relations les valeurs numériques utilisées dans l'exercice traité par Excel ... les courbes tracées de y = f(x) sont identiques (à rien près).
Sauf distraction. 


