Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie AutreForum traitant de la physique ou de la chimie, mais sur des thèmes un peu moins scolaires PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Forum Autre
Partager :

Balistique

Posté par
goundour 12-03-13 à 20:07

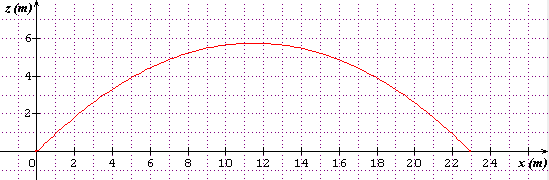
Bonjour j'ai une courbe représentative du lancer d'un projectile a 15m/s ; d'angle 45°

J'aimerais savoir l'équation de la trajectoire, la Flèche.
j'ai déjà essayé pleins de fois et je trouve pour l'équation : -0.0456x²+1.0456x+0 elle semble correspondre
en revanche pour la flèche je n'y arrive pas
merci d'avence

Balistique

Edit Coll : forum modifié

Posté par
Coll Moderateurre : Balistique 12-03-13 à 20:14

Bonsoir,

D'où sort cette équation ?
Comment as-tu fait pour la déterminer ?

Posté par
Coll Moderateurre : Balistique 12-03-13 à 20:30

Ta courbe est à peu près illisible.
Ressemble-t-elle à ceci ?

Balistique

Posté par
goundourre : Balistique 12-03-13 à 20:35

oui elle est illisible car je l'ai réduite pour qu elle fasse moins de 80Ko
α=0 et β=22.94
f(x)=a(x-α)(x-β)
donc f(x)=ax(x-22.94)
f(x)=a(x²-22.94x)
par ailleur on lit f(1)=1              (j'ai pris 1 a peu pres ...)
                or f(1)=a(-21.94)
                dc a = -0.04557885141
                   b = +1.045578851
                   c = 0

Posté par
Coll Moderateurre : Balistique 12-03-13 à 20:46



Ça, ce sont des mathématiques... ajustement d'une équation à une courbe ! Pas de la physique !
Je reconnais que tu t'es assez bien débrouillé(e).

Mais je suppose que c'est un exercice de physique et pas de mathématiques...
_________

Quand le projectile est en l'air, on suppose qu'il n'est soumis qu'à une seule force, laquelle ?

En appliquant la seconde loi de Newton, que peut-on en déduire pour son accélération ? \vec{a}

Connaissant son accélération et sa vitesse initiale, quelles sont les composantes de sa vitesse \vec{v}(t) en fonction du temps ? vx(t) et vy(t)

Et donc, quelles sont les composantes de sa position en fonction du temps ? x(t) et y(t)

De ces composantes on peut déduire l'équation de la trajectoire : y(x)

et bien sûr, la flèche.

Posté par
goundourre : Balistique 12-03-13 à 20:52

En faite c'est pour un TPE : je n'ai pas encore vu cela ...
Peut on partir du principe que ma fonction est bonne et en déduire la flèche ?

Posté par
Coll Moderateurre : Balistique 13-03-13 à 08:08

La solution en physique :

Une fois lancé, le projectile M (si l'on néglige poussée d'Archimède et résistance de l'air) n'est plus soumis qu'à une seule force : son poids \vec{P}\;=\;m.\vec{g}

D'après la seconde loi de Newton il est donc soumis à une accélération \vec{a} telle que \vec{a}\;=\;\frac{\vec{F}}{m}\;=\;\frac{\vec{P}}{m}\;=\;\vec{g}

Adoptons comme repère un repère orthonormé, d'origine O, le point de lancement, d'axe horizontal Ox, orienté dans la direction du lancement, et d'axe vertical, orienté vers le haut, Oz

Coordonnées de l'accélération :

\large \vec{a}\ :\ \begin{array}{|c} 0 \\ - g\end{array}

En notant g l'intensité de l'accélération due à la pesanteur (qui vaut environ 9,8 m.s-2 en France à basse altitude)

On en déduit, en cherchant les primitives, les coordonnées du vecteur vitesse \vec{v}(t) :

\large \vec{v}(t)\ :\ \begin{array}{|c} constante_1 \\ - g.t \,+\, constante_2\end{array}

Pour déterminer les valeurs des constantes on prend en compte la vitesse initiale \vec{v}(0) (vitesse pour t = 0 s )
Or, d'après l'énoncé, le projectile est lancé avec une vitesse :
. dont la direction fait un angle de 45° avec l'horizontale
. dont le sens est vers le haut ( ! )
. dont l'intensité est de 15 m.s-1

Si bien que cette vitesse initiale \vec{v}(0) vaut (l'unité est le mètre par seconde) :

\large \vec{v}(0)\ :\ \begin{array}{|c} 15.\cos(45°) \\ 15.\sin(45°)\end{array}

En conséquence, la vitesse en fonction du temps vaut :

\large \vec{v}(t)\ :\ \begin{array}{|c} 15.\cos(45°) \\ - g.t\, +\, 15.\sin(45°)\end{array}

Pour connaître la position \vec{OM}(t) du projectile M en fonction du temps, il faut chercher des primitives à la vitesse :

\large \vec{OM}(t)\ :\ \begin{array}{|c} 15.\cos(45°).t\,+\,constante_3 \\ -\frac{1}{2} g.t^2\, +\, 15.\sin(45°).t\,+\,constante_4\end{array}

Les valeurs des deux constantes sont déterminées en prenant en considération la position du projectile à l'instant initial :

\large \vec{OM}(0)\ :\ \begin{array}{|c} 0 \\ 0\end{array}

Et donc la position \vec{OM}(t) du projectile en fonction du temps t vaut :

\large \vec{OM}(t)\ :\ \begin{array}{|c} x(t)\;=\;15.\cos(45°).t \\ z(t)\;=\;-\frac{1}{2} g.t^2\, +\, 15.\sin(45°).t\end{array}

Ceci pour t 0 s et aussi longtemps que le projectile n'a pas rejoint le sol.

On en déduit l'équation de la trajectoire (en "éliminant" t entre les deux équations x(t) et z(t) )

\Large y(x)\;=\;-\frac{1}{2}.g.\frac{x^2}{(15.\cos(45°) )^2}\;+\;\frac{15.\sin(45°).x}{15.\cos(45°)}

soit

\Large y(x)\;=\;-\frac{g.x^2}{15^2}\;+\;x

adoptant g = 9,8 m.s-2

l'équation de la trajectoire devient :

\Large \red \boxed{ y(x)\;\approx\;-0,043\,6.x^2\;+\;x}

La flèche s'obtient en cherchant la cote du point le plus haut de la trajectoire.
Parmi les méthodes possibles :
En ce point la vitesse verticale cesse d'être positive pour devenir négative ; elle est nulle, donc

- g.t + 15.sin(45°) = 0
ou
t = 15.sin(45°) / g
c'est l'instant où le projectile est au plus haut

À cet instant, sa cote vaut :

z(t) = -\frac{1}{2}.g.\frac{(15.\sin(45°) )^2}{g^2}\;+\;15.sin(45°).\frac{15.\sin(45°)}{g}

et donc la flèche, f, vaut :

\Large \red \boxed {f\; =\; \frac{(15.\sin(45°) )^2}{2.g}}

Application numérique : f 5,74 m

Posté par
goundourre : Balistique 13-03-13 à 18:34

Vraiment un gros merci

Tu a du y passer un bon moment a écrire tout sa

Posté par
Coll Moderateurre : Balistique 13-03-13 à 18:55

J'ai écrit des y là où j'aurais dû écrire des z.

Je corrige ci-dessous :

Citation :
On en déduit l'équation de la trajectoire (en "éliminant" t entre les deux équations x(t) et z(t) )

\Large z(x)\;=\;-\frac{1}{2}.g.\frac{x^2}{(15.\cos(45°) )^2}\;+\;\frac{15.\sin(45°).x}{15.\cos(45°)}

soit

\Large z(x)\;=\;-\frac{g.x^2}{15^2}\;+\;x

adoptant g = 9,8 m.s-2

l'équation de la trajectoire devient :

\Large \red \boxed{ z(x)\;\approx\;-0,043\,6.x^2\;+\;x}

_____________

Je t'en prie et à une prochaine fois !

Posté par
goundourre : Balistique 14-03-13 à 20:28

Merci ça me sera vraiment très utile

Posté par
Coll Moderateurre : Balistique 14-03-13 à 20:30

Je t'en prie.
À une prochaine fois !

Posté par
goundourTirer le plus loin 21-03-13 à 23:16

Bonjour j'aurais vraiment besoin que quelqu'un m'aide a trouver la démonstration qui montre que 45° est le meilleur angle (force de frottement de l'air négligé) pour qu'un projectile aille le plus loin, car la je suis un peu pommé

Merci d'avance.

*** message déplacé ***

Posté par
Coll Moderateurre : Balistique 22-03-13 à 08:02

Il suffit de refaire le calcul mais cette fois-ci sans imposer à l'angle entre la vitesse et l'horizontale de valoir 45°

Je recopie la démonstration précédente :

Une fois lancé, le projectile M (si l'on néglige poussée d'Archimède et résistance de l'air) n'est plus soumis qu'à une seule force : son poids \vec{P}\;=\;m.\vec{g}

D'après la seconde loi de Newton il est donc soumis à une accélération \vec{a} telle que \vec{a}\;=\;\frac{\vec{F}}{m}\;=\;\frac{\vec{P}}{m}\;=\;\vec{g}

Adoptons comme repère un repère orthonormé, d'origine O, le point de lancement, d'axe horizontal Ox, orienté dans la direction du lancement, et d'axe vertical, orienté vers le haut, Oz

Coordonnées de l'accélération :

\large \vec{a}\ :\ \begin{array}{|c} 0 \\ - g\end{array}

En notant g l'intensité de l'accélération due à la pesanteur (qui vaut environ 9,8 m.s-2 en France à basse altitude)

On en déduit, en cherchant les primitives, les coordonnées du vecteur vitesse \vec{v}(t) :

\large \vec{v}(t)\ :\ \begin{array}{|c} constante_1 \\ - g.t \,+\, constante_2\end{array}

Pour déterminer les valeurs des constantes on prend en compte la vitesse initiale \vec{v}(0) (vitesse pour t = 0 s )
Le projectile est lancé avec une vitesse :
. dont la direction fait un angle avec l'horizontale
. dont le sens est vers le haut
. dont l'intensité vaut v(0) = v0

Si bien que cette vitesse initiale \vec{v}(0) vaut (l'unité est le mètre par seconde) :

\large \vec{v}(0)\ :\ \begin{array}{|c} v_0.\cos(\alpha) \\ v_0.\sin(\alpha)\end{array}

En conséquence, la vitesse en fonction du temps vaut :

\large \vec{v}(t)\ :\ \begin{array}{|c} v_0.\cos(\alpha) \\ - g.t\, +\, v_0.\sin(\alpha)\end{array}

Pour connaître la position \vec{OM}(t) du projectile M en fonction du temps, il faut chercher des primitives à la vitesse :

\large \vec{OM}(t)\ :\ \begin{array}{|c} v_0.\cos(\alpha).t\,+\,constante_3 \\ -\frac{1}{2} g.t^2\, +\, v_0.\sin(\alpha).t\,+\,constante_4\end{array}

Les valeurs des deux constantes sont déterminées en prenant en considération la position du projectile à l'instant initial :

\large \vec{OM}(0)\ :\ \begin{array}{|c} 0 \\ 0\end{array}

Et donc la position \vec{OM}(t) du projectile en fonction du temps t vaut :

\large \vec{OM}(t)\ :\ \begin{array}{|c} x(t)\;=\;v_0.\cos(\alpha).t \\ z(t)\;=\;-\frac{1}{2} g.t^2\, +\, v_0.\sin(\alpha).t\end{array}

Ceci pour t 0 s et aussi longtemps que le projectile n'a pas rejoint le sol.

Or, le projectile est au niveau du sol quand z(t) = 0

\large z(t)\;=\;[-\frac{1}{2} g.t\, +\, v_0.\sin(\alpha)].t

z(t) = 0 pour deux instants :

t = 0 s (c'est évident : on retrouve la position de départ ! )
et
\large t\;=\;\frac{2.v_0.\sin(\alpha)}{g}

Les abscisses du mobile sont à ces deux instants :

Pour t = 0 s :
x(0) = 0 m (c'est l'origine)

et
pour \large t\;=\;\frac{2.v_0.\sin(\alpha)}{g}

\large x(t)\;=\;\frac{v_0^2.2.\sin(\alpha).\cos(\alpha)}{g}\;=\;\frac{v_0^2.\sin(2\alpha)}{g}

Cette dernière valeur est donc la portée du lancer

Pour une intensité donnée de la vitesse v0, cette portée sera maximale pour la valeur maximale de sin(2), c'est-à-dire pour sin(2) = 1
c'est-à-dire 2 = 90°, et donc

\large \red \boxed{\alpha\;=\;45°}

Posté par
goundourre : Balistique 22-03-13 à 18:00

Merci sa m'a débloqué

Posté par
Coll Moderateurre : Balistique 22-03-13 à 19:00


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !