Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Avion avec des ailes non symétriques

Posté par
julienh 29-05-18 à 14:28

Bonjour,
Je cherche à montrer qu'un avion (que je vais considérer comme deux ailes reliées à un cockpit qui sera mon axe de rotation) qui a des ailes non symétriques (par exemple de longueurs différentes ) va tourner sur lui même.
Pour cela je me suis intéressé aux effets des forces de frottements sur ses ailes.
L'avion vole en ligne droite à vitesse constante dans un milieu homogène.

Ec = Energie cinétique de mon avion
x'= vitesse de mon avion
p=masse volumique du milieu
S=la surface avant (de mon avion) en contact avec l'air
m=masse des molécules du milieu

Je pars du principe que à chaque molécules rencontrées, l'avion transmet sa vitesse à ces molécules, et donc son énergie cinétique par mètre parcouru  varie tel que chaque molécules rencontrée reçois une énergie cinétique proportionnelles à leurs masses et la vitesse de l'avion.

J'ai donc pour mon avion:

\frac{dEc}{dx}=-(\frac{S*p}{m})*(0.5*m*\dot{x}^2)

En multipliant par dx des deux côtés et en dérivant par rapport au temps, j'obtiens au final pour ma force de frottements s'appliquant sur mon avion:
\vec{F}=-S*p*0.5*\dot{x}^2*\vec{Ux}

Je cherche donc maintenant à calculer la somme des moments de forces s'appliquant sur les deux ailes.
Pour cela j'utilise la méthode que "Vanoise" (que je remercie encore) m'a très bien expliqué dans ce sujet:
https://www.ilephysique.net/sujet-calcul-du-moment-de-force-sur-une-surface-301201.html

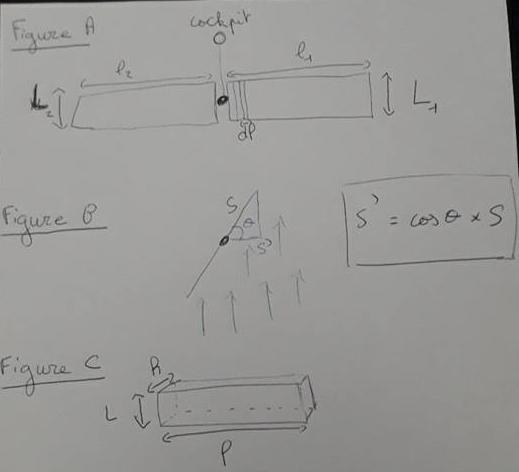
Je découpe comme dans la figure A mes ailes d'avions comme des petites surfaces :
dS= dl *L

l (1,2) = longueur de l'aile (1,2)
L (1,2) =largeur de l'aile (1,2)

De plus comme montré dans la figure B, la force de frottement dépend de la surface présenté de front par l'avion, ainsi si mes ailes ne sont pas de front et décalés d'un angles \theta cette surface diminue :
Nous avons donc : d\vec{F}=-cos(\theta )*dl*L*p*0.5*\dot{x}^2*\vec{Ux}

\vec{M} = somme des moments de forces

or : \sum{\vec{M}}= \int_{0}^{-l2}{\vec{l}\Lambda \vec{df}}+ \int_{0}^{l1}{\vec{l}\Lambda \vec{df}}

\Leftrightarrow  \sum{\vec{M}}= -\int_{0}^{l2}{sin(\theta)cos(\theta )*l*dl*L_{2}*p*0.5*\dot{x}^2*\vec{k}}+ \int_{0}^{l1}{sin(\theta)cos(\theta )*l*dl*L_{1}*p*0.5*\dot{x}^2*\vec{k}}
\Leftrightarrow  \sum{\vec{M}}= (\frac{l_{1}^2*L_{1}}{2}-\frac{l_{2}^2*L_{2}}{2})sin(\theta)cos(\theta )*p*0.5*\dot{x}^2*\vec{k}

or : \frac{d\sum{\vec{L}}}{dt}=\sum{\vec{M}}

L est le moment cinétique.

Pour calculer cette somme de moments cinétiques, je considère maintenant mes deux ailes comme des pavés pleins et homogènes, de longueur l, hauteur L et profondeur h (Figure C).   Et dm est une petite masse à un endroit donné de mon aile et q la masse volumique de mon aile.

d\vec{L}=\vec{l}\Lambda (dm*l*\dot{\theta }*\vec{Ux})
\Leftrightarrow d\vec{L}=l^2*\dot{\theta }*q*dh*dl*dL*\vec{k}

\Leftrightarrow \sum{\vec{L}}=\int_{0}^{h1}\int_{0}^{L1}\int_{0}^{l1}{l^2*\dot{\theta }*q*dh*dl*dL*\vec{k} }+\int_{0}^{h2}\int_{0}^{L2}\int_{0}^{-l2}{l^2*\dot{\theta }*q*dh*dl*dL*\vec{k} }

\Leftrightarrow \sum{\vec{L}}=q\dot{\theta }(\frac{l_{1}^3}{3}*h_{1}*L_{1}-\frac{l_{2}^3}{3}*h_{2}*L_{2})\vec{k}

\Leftrightarrow\frac{d \sum{\vec{L}}}{dt}=q\ddot{\theta }(\frac{l_{1}^3}{3}*h_{1}*L_{1}-\frac{l_{2}^3}{3}*h_{2}*L_{2})\vec{k}

or : \frac{d\sum{\vec{L}}}{dt}=\sum{\vec{M}}

\Leftrightarrow q\ddot{\theta }(\frac{l_{1}^3}{3}*h_{1}*L_{1}-\frac{l_{2}^3}{3}*h_{2}*L_{2})\vec{k} = (\frac{l_{1}^2*L_{1}}{2}-\frac{l_{2}^2*L_{2}}{2})sin(\theta)cos(\theta )*p*0.5*\dot{x}^2*\vec{k}

\Leftrightarrow q\ddot{\theta }(\frac{l_{1}^3}{3}*h_{1}*L_{1}-\frac{l_{2}^3}{3}*h_{2}*L_{2})\vec{k} = (\frac{l_{1}^2*L_{1}}{2}-\frac{l_{2}^2*L_{2}}{2})\frac{sin(2\theta )}{2}*p*0.5*\dot{x}^2*\vec{k}


Et donc  pour finir:
\Leftrightarrow \ddot{\theta }=sin(2\theta )* \frac{(\frac{l_{1}^2*L_{1}}{2}-\frac{l_{2}^2*L_{2}}{2})\frac{1}{2}*p*0.5*\dot{x}^2 }{q(\frac{l_{1}^3}{3}*h_{1}*L_{1}-\frac{l_{2}^3}{3}*h_{2}*L_{2})}

A=\frac{(\frac{l_{1}^2*L_{1}}{2}-\frac{l_{2}^2*L_{2}}{2})\frac{1}{2}*p*0.5*\dot{x}^2 }{q(\frac{l_{1}^3}{3}*h_{1}*L_{1}-\frac{l_{2}^3}{3}*h_{2}*L_{2})} \\ \\ \\ \Leftrightarrow \ddot{\theta }=sin(2\theta ) * A

Si on suppose que  \theta  est petit on a:

\Leftrightarrow \ddot{\theta }=\theta  * A°

A°=2*A

et donc  \theta(t)  = C_{1}*e^{\sqrt{A°}*t}* C_{2}*e^{-\sqrt{A°}*t}

Mais là où ça coince c'est que je m'attendais à trouver dans le cas où les deux ailes sont identiques (l1=l2 , L1=L2 et h1=h2)  un \ddot{\theta } égal à 0 pour tous t... ce qui n'est pas le cas car A ne sera pas égal à 0 mais une constant ...

Toutes ces notions sont assez nouvelles pour moi (nous avons vu en cours que des cas à un point) , donc je suppose que j'ai surement fais des erreurs de raisonnements.
En tous cas merci d'avance pour toutes aides .

Bonne journée.

Avion avec des ailes non symétriques

Posté par
vanoisere : Avion avec des ailes non symétriques 29-05-18 à 15:20

Bonjour
Quand un avion vole à l'horizontale (vitesse colinéaire à un axe (Ox)), chaque aile est soumise à deux forces :
une force de portance verticale ascendante qui empêche l'avion de tomber en s'opposant au poids ;
une force de frottement appelée force de traînée.
Ces deux types de forces sont proportionnelles au carré de la vitesse.
Imagine une aile plus courte que l'autre. Les moments des forces de traînées tendent effectivement à faire tourner l'avion autour d'un axe vertical. Le calcul que tu as fait doit prendre en compte la vitesse d'un point de l'aile par rapport à la terre (absence de vent), cette vitesse dépendant à la fois de la vitesse de translation de l'avion et de la vitesse de rotation propre due au virage... Pas très simple...
Les deux forces de portance vont aussi être différentes, entraînant une rotation de l'avion autour de l'axe (Ox)...
Quelques schémas et précisions ici :

Posté par
julienhre : Avion avec des ailes non symétriques 29-05-18 à 16:27

Tout d'abord merci pour votre réponse.

Citation :
chaque aile est soumise à deux forces :
une force de portance verticale ascendante qui empêche l'avion de tomber en s'opposant au poids ; une force de frottement appelée force de traînée


Si je ne me trompe pas, un défaut (par exemple les moments de forces pas égaux des deux côtés de l'avion et ne se compensant pas avec le poids) dans la force ascendante entraînera une rotation selon Ox, et un défaut dans la force de traînée entraînera une rotation selon k.

Si je me place dans un cas très simple  où on ne prends pas en compte les rotations selon Ox, et où j'étudie seulement les rotations selon k,  je peux par exemple supposer que mon avion est comme une planche autour d'un axe (comme par exemple un  girouette). Et ainsi je me retrouve avec l'interprétation  que je faisais dans mon premier message. Et de plus la force de frottement que j'utilise est la même que la force de traîné dont parle le site, à un coefficient prêt.

Je n'ai pas très bien compris par contre ce que vous voulais dire par:

Citation :
Le calcul que tu as fait doit prendre en compte la vitesse d'un point de l'aile par rapport à la terre (absence de vent), cette vitesse dépendant à la fois de la vitesse de translation de l'avion et de la vitesse de rotation propre due au virage


J'essaie en fait de faire un petit exposé (une vidéo de 3mn) pour ma classe, avec des connaissance de L1, je veux juste donner idée de pourquoi l'avion tourne sur lui même si il n'est pas symétrique. Je me vois donc mal introduire toutes les notions du site qui m'ont l'air assez complexes...

Merci encore et bonne journée

Posté par
vanoisere : Avion avec des ailes non symétriques 29-05-18 à 16:58

Pour faire très simple (trop simple ?), on peut imaginer uniquement une rotation autour d'un axe vertical (O,z), le point O se déplaçant à la vitesse horizontale \overrightarrow{V}=V.\overrightarrow{u_{x}}. L'avion tourne autour de l'axe vertical (O,z) à la vitesse angulaire \dot{\theta}. On travaille en coordonnées polaires et on note r la distance d'un point de l'aile à l'axe du cockpit.
La tranche élémentaire d'aile droite située entre r et r+dr est animée par rapport à la terre, donc par rapport à l'air si on suppose l'absence de vent, de la vitesse :
\overrightarrow{v}=V.\overrightarrow{u_{x}}+r.\dot{\theta}.\overrightarrow{u_{\theta}}
Cette tranche élémentaire d'aile droite est soumise à une force de traînée élémentaire qui peut s'écrire sous la forme :
\overrightarrow{dF}=-k.\Vert\overrightarrow{v}\Vert.\overrightarrow{v}.dr
L'aile est plus épaisse au voisinage du cockpit. k décroît en fonction de r. Dans une première approche, tu peux considérer k comme une constante qui dépend de la masse volumique de l'air, de l'épaisseur de l'aile et de son profil. Le moment élémentaire en O de cette force est :
\overrightarrow{dM_d}=r.\overrightarrow{u_{r}}\wedge\overrightarrow{dF}
Il te faut ensuite intégrer entre ro et (ro+ld) où ld est la longueur de l'aile droite, ro la distance de l'extrémité de l'aile au centre O.
Il faut ensuite adapter le raisonnement au cas de l'aile gauche (changement de signe dans l'expression du vecteur vitesse)...
Bon courage !

Posté par
julienhre : Avion avec des ailes non symétriques 29-05-18 à 17:27

Cette méthode est justement celle que je pense avoir faite pour le calcul de ma somme de moments de forces  (il y a juste le cos(θ) que j'ai rajouté en plus par rapport au fait que quand l'aile tourne il y a moins de prise au vent).

Et le problème est que à la fin, après avoir comparé la somme des moments de forces à la dérivée de mon moment cinétique, si mes deux ailes ont la même forme mon terme A va s'exprimer la forme : A=c_{1}*\frac{l_{1}^2-l_{2}^2}{l_{1}^3-l_{2}^3} avec l1 qui tend vers l2, ce qui me donnera une valeur quelconque pour A, ce qui ne me permet pas de conclure pour une non rotation de l'avion si les ailes sont symétriques

Posté par
vanoisere : Avion avec des ailes non symétriques 29-05-18 à 18:30

Pour simplifier un peu, on peut considérer que seule la composante de la vitesse perpendiculaire à l'aile, donc la composante de la vitesse suivant \overrightarrow{u_{\theta}} , intervient dans l'expression de la force de traînée. Cela fait intervenir un terme en cos() mais la vitesse de rotation propre (r.\dot{\theta}) intervient aussi. Ainsi l'extrémité de l'aile tourne plus vite que la partie proche du cockpit. Cela donne pour l'aile droite :
\overrightarrow{dF}=-k.\left[V.\cos\left(\theta\right)+r.\dot{\theta}\right]^{2}.\overrightarrow{u_{\theta}}.dr \\ \\ \overrightarrow{dM_d}=r.\overrightarrow{u_{r}}\wedge\overrightarrow{dF}
Effectue le calcul de ce moment ; adapte-le pour l'aile gauche. Tu constateras que, si les deux ailes sont de longueurs différentes, la somme des deux moments n'est pas le vecteur nul.
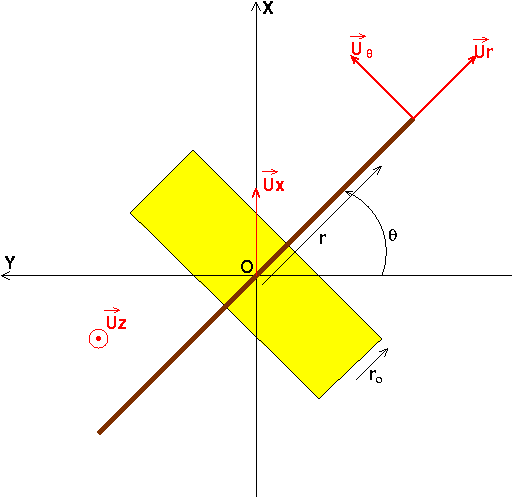
Ci-dessous, une vue de dessus de l'avion extrêmement schématisé : le cockpit par un rectangle jaune et chaque axe d'aile par un trait marron... L'intérêt réside plutôt dans les orientations des vecteurs unitaires et la définition de .

Avion avec des ailes non symétriques

Posté par
julienhre : Avion avec des ailes non symétriques 29-05-18 à 22:01

Ok merci, j'avais complètement oublié que le mouvement de rotation est lui aussi amorti.

Donc en intégrant je me retrouve avec:
\sum{\vec{M}}= k*((l_{1}-l_{2})*\dot{x}^2*cos^2(\theta)+(l_{1}^2-l_{2}^2)*\dot{\theta}*\dot{x}+(l_{1}^3-l_{2}^3)*\frac{1}{3}*\dot{\theta})sin(\theta)*\vec{Uz}

  et donc en comparant avec la dérivée du moment cinétique:
\sum{\vec{M}}= k*((l_{1}-l_{2})*\dot{x}^2*cos^2(\theta)+(l_{1}^2-l_{2}^2)*\dot{\theta}*\dot{x}+(l_{1}^3-l_{2}^3)*\frac{1}{3}*\dot{\theta})sin(\theta)*\vec{Uz} =q\ddot{\theta }(\frac{l_{1}^3}{3}*h_{1}*L_{1}-\frac{l_{2}^3}{3}*h_{2}*L_{2})\vec{Uz}


Mais \ddot{\theta} n'est donc toujours pas forcément nul si l1 = l2  ...

Posté par
vanoisere : Avion avec des ailes non symétriques 29-05-18 à 22:33

On constate immédiatement que, dans le cas particulier l1=l2, la somme des 2 moments est le vecteur nul. La traînée n'a aucune influence sur une éventuelle rotation autour de l'axe (Oz) dans ce cas particulier.

Posté par
julienhre : Avion avec des ailes non symétriques 29-05-18 à 23:51

Oui excusez moi ,  car j'étais resté bloqué sur le fait que la limite de  (l1^2 - l2^2)/(l1^3-l2^3) tendait vers une limite finie, mais le problème  ne se pose pas car à l'état initial  \dot{\theta}  = 0 .


Merci encore pour toutes vos aides, bonne continuation

Posté par
vanoisere : Avion avec des ailes non symétriques 30-05-18 à 15:34

Bonjour
Je t'ai répondu hier soir un peu vite sans prendre le temps de vérifier tes calculs et j'ai eu tort : tu as commis plusieurs erreurs. Je reprends tout cela avec mes notations du message d'hier 18h30.
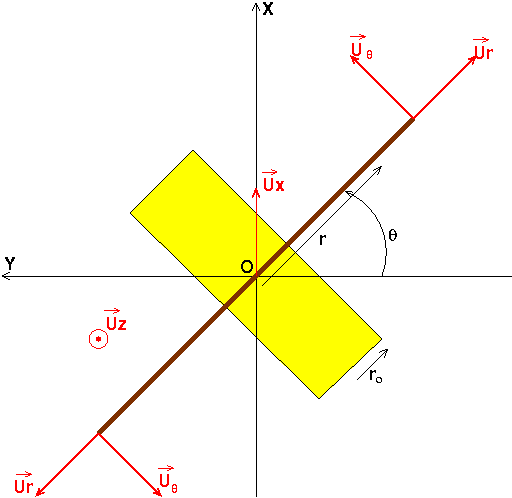
Pour l'aile droite :

\overrightarrow{dM_{d}}=r.\overrightarrow{u_{r}}\wedge\overrightarrow{dF}=-k\left[V^{2}.\cos^{2}\left(\theta\right).r+r^{3}.\dot{\theta}^{2}+2.V.\dot{\theta}.\cos\left(\theta\right).r^{2}\right].dr.\overrightarrow{u_{z}}

\overrightarrow{M_{d}}=-k.\overrightarrow{u_{z}}.\left[V^{2}.\cos^{2}\left(\theta\right).\frac{r^{2}}{2}+\frac{r^{4}}{4}.\dot{\theta}^{2}+2.V.\dot{\theta}.\cos\left(\theta\right).\frac{r^{3}}{3}\right]_{r_{\text{0}}}^{r_{0}+l_{d}}
Pour l'aile gauche : les vecteurs \overrightarrow{u_{r}} et \overrightarrow{u_{\theta}} ont même directions que précédemment mais leurs sens sont inversés. La vitesse d'une tranche d'aile comprise entre les distances r et (r+dr) du cockpit par rapport à l'air s'écrit toujours :

\overrightarrow{v}=V.\overrightarrow{u_{x}}+r.\dot{\theta}.\overrightarrow{u_{\theta}}

mais la composante de V.\overrightarrow{u_{x}} sur \overrightarrow{u_{\theta}} est de signe opposé. Cela conduit à :

\overrightarrow{dF}=k.\left[V.\cos\left(\theta\right)-r.\dot{\theta}\right]^{2}.\overrightarrow{u_{\theta}}.dr

\overrightarrow{dM_{g}}=r.\overrightarrow{u_{r}}\wedge\overrightarrow{dF}=k\left[V^{2}.\cos^{2}\left(\theta\right).r+r^{3}.\dot{\theta}^{2}-2.V.\dot{\theta}.\cos\left(\theta\right).r^{2}\right].dr.\overrightarrow{u_{z}}

\overrightarrow{M_{g}}=k.\overrightarrow{u_{z}}.\left[V^{2}.\cos^{2}\left(\theta\right).\frac{r^{2}}{2}+\frac{r^{4}}{4}.\dot{\theta}^{2}-2.V.\dot{\theta}.\cos\left(\theta\right).\frac{r^{3}}{3}\right]_{r_{\text{0}}}^{r_{0}+l_{g}}

Il faut calculer alors la somme des deux moments. On constate que cette somme est le vecteur nul pour des longueurs d'ailes identiques et pour une vitesse de rotation \dot{\theta} nulle. Inutile à mon avis de faire intervenir le théorème du moment cinétique. D'ailleurs, il ne peut s'appliquer ici simplement que si le point O est confondu avec le centre d'inertie G de l'avion.

Remarque : il aurait sans doute été plus simple et suffisant de déterminer le moment de la force de traînée en imaginant le mouvement de l'avion rectiligne (\theta=0\quad;\quad\dot{\theta}=0). On obtient alors simplement :

\overrightarrow{M}=\overrightarrow{M_{g}}+\overrightarrow{M_{d}}=k.V^{2}.\overrightarrow{u_{z}}\left(\frac{\left(r_{0}+l_{g}\right)^{2}-\left(r_{0}+l_{d}\right)^{2}}{2}\right)=\frac{1}{2}k.V^{2}.\overrightarrow{u_{z}}.\left(2r_{0}+l_{g}+l_{d}\right).\left(l_{g}-l_{d}\right)

On voit bien que ce moment est le vecteur nul si les deux ailes sont de longueurs identiques et que la traînée provoque une rotation dans le sens trigonométrique (pour un spectateur placé au dessus de l'avion) si l'aile gauche est la plus longue.

Avion avec des ailes non symétriques

Posté par
julienhre : Avion avec des ailes non symétriques 03-06-18 à 12:28

Tout d'abord désolé pour ma réponse tardive (je n'avais pas vu que vous m'aviez répondu une nouvelle fois).

Merci pour cette réponse, je m'étais embrouillé avec mes vecteurs, d'ailleurs j'avais quasiment fais exactement la même erreur dans mon calcul du moment cinétique (ou j'avais considéré un -l2 alors que \ vec{U_{\theta}}[\tex] était orienté en sens inverse de l1) ce qui me donnait un moment cinétique qui s'annulait quand les deux ailes étaient identiques, ce qui était la principale cause de mon incompréhension du problème. \\ \\ Pour le calcul des moments de forces que vous faites ici, je n'avais pas pensé que l'avion tournait tout entier (donc son vecteur vitesse aussi) , et pas seulement ses ailes ce qui était la raison pour laquelle j'avais rajouté le [tex]sin(\theta )  pour le produit vectoriel.


En tous cas, encore merci pour toutes l'aide que vous m'avez apporté. Cela ne vous dérange pas si je réutilise votre schéma qui est très clair pour ma présentation ?

Merci encore, bonne continuation


En tout cas merci pour toute

Posté par
julienhre : Avion avec des ailes non symétriques 03-06-18 à 12:30

Tout d'abord désolé pour ma réponse tardive (je n'avais pas vu que vous m'aviez répondu une nouvelle fois).

Merci pour cette réponse, je m'étais embrouillé avec mes vecteurs, d'ailleurs j'avais quasiment fais exactement la même erreur dans mon calcul du moment cinétique (ou j'avais considéré un -l2 alors que \vec{U_{\theta}} était orienté en sens inverse de l1) ce qui me donnait un moment cinétique qui s'annulait quand les deux ailes étaient identiques, ce qui était la principale cause de mon incompréhension du problème.

Pour le calcul des moments de forces que vous faites ici, je n'avais pas pensé que l'avion tournait tout entier (donc son vecteur vitesse aussi) , et pas seulement ses ailes ce qui était la raison pour laquelle j'avais rajouté le sin(\theta )  pour le produit vectoriel.


En tous cas, encore merci pour toutes l'aide que vous m'avez apporté. Cela ne vous dérange pas si je réutilise votre schéma qui est très clair pour ma présentation ?

Merci encore, bonne continuation


En tout cas merci pour toute

Posté par
vanoisere : Avion avec des ailes non symétriques 03-06-18 à 23:00

Citation :
Cela ne vous dérange pas si je réutilise votre schéma qui est très clair pour ma présentation ?

Aucun problème !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !