Bonjour,

aide-toi de cette fiche : Mouvement d'un projectile dans le champ de pesanteur

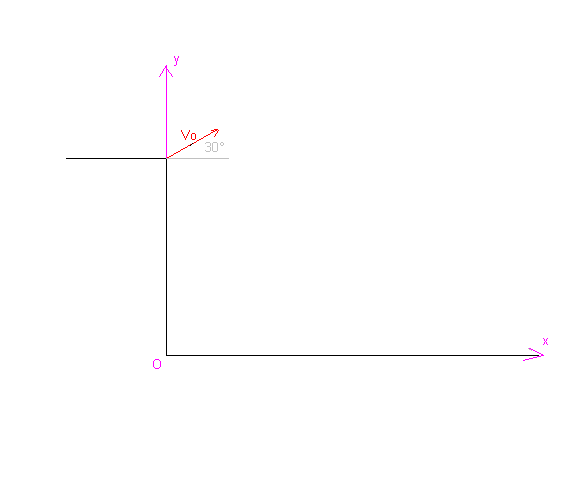
Avec le repère représenté, x et y étant les coordonnées du centre d'inertie de la balle.
L'origine des temps étant à l'instant du lancé de la balle.

x(t) = Vo.cos(30°).t
y(t) = yo + vo.sin(30°).t - gt²/2

x(t) = 21.cos(30°).t
y(t) = 16 + 21.sin(30°).t - 9,8.t²/2

x(t) = 18,18.t
y(t) = 16 + 10,5.t - 4,9.t²

a)
La balle touche le sol pour y(t) = 0 avec t > 0 -->
16 + 10,5.t - 4,9.t² = 0
t = 3,17 s

b)
Portée = x(3,17) = 18,18*3,17 = 10 m

c)
y(t) = 16 + 10,5.t - 4,9.t²
y'(t) = 10,5 - 9,8 t
y est max en t = 10,5/9,8 = 1,07 s
ymax = y(1,07) =  16 + 10,5*1,07 - 4,9*1,07² = 21,6 m

d)
x(t) = 18,18.t
y(t) = 16 + 10,5.t - 4,9.t²

x'(t) = 18,18
y'(t) = 10,5 - 9,8t

x'(3,17) = 18,18
y'(3,17) = 10,5 - 9,8t = -20,57

tan(beta) = -20,57/18,18
|beta| = 48,5°

e)
y = 16+2 = 18 m
18 = 16 + 10,5.t - 4,9.t²
-2 + 10,5.t - 4,9.t² = 0
--> t = 0,211 s ou t = 1,932 s

x'(0,211) = 18,18 m/s
y'(0,211) = 10,5 - 9,8*0,211 = 8,43 m/s  
vitesse = racinecarrée(18,18² + 8,43²) = 20 m/s

On trouvera pareillement:
x'(1,932) = 18,18 m/s
y'(1,932) = 10,5 - 9,8*1,932 = -8,43 m/s  
vitesse = racinecarrée(18,18² + 8,43²) = 20 m/s
-----
Penser à arrondir les réponses pour le nombre de chiffres significatifs si c'est attendu).

Plusieurs des réponses ci-dessus peuvent être trouvée par une autre méthode (conservation de l'énergie mécanique de la balle pendant sa trajectoire avanr de toucher le sol).

Sauf distraction.  

Salut J-P,

tu as eu le courage de tout refaire .

Merci beaucoup pour le raisonnement