Inscription / Connexion Nouveau Sujet
association filtres circuit RLC
Bonjour tout le monde !
alors voilà j'ai un petit souci concernant un exercice d'association de filtre.
On n'a pas encore fais le cours sur l'association de filtre
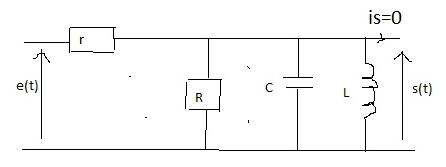
je vous poste le schéma du filtre
1)je devais trouver la nature probable du filtre représenté
j'ai trouvé que ce pouvais être un passe bande.
2) Déterminer l'expression de la fonction de transfert H barre
Et c'est la que j'ai un petit souci :/
faut-il que je trouve l'impédance équivalente et que je fasse un pont diviseur de tension ?
voila je suis un peu perdu
merci 
je viens de lire sur internet qu'en général quand on a deux filtres en cascade, la fonction de transfert totale est le produit des 2 fonctions de transferts.
Mais quand peut-on appliquer ce cas ?
Bonjour,
ça, ça marche dans le cas idéal. En particulier avec une impédance d'entrée infinie.
Ici, tu as bien s/e=Z/(r+Z).
Impédance du R // C // L
1/Z = 1/R + jwC + 1/(jwL)
1/Z = (jwL - w²RLC + R)/(jwRL)
Z = jwLR/(R.(1-w²LC)+jwL)
e/(r+Z) = s/Z
s/e = Z/(r+Z)
s/e = [ jwLR/(R.(1-w²LC)+jwL)]/[r + jwLR/(R.(1-w²LC)+jwL)]
s/e = jwLR/[r.(R.(1-w²LC)+jwL) + jwLR]
s/e = jwLR/(Rr.(1-w²LC) + jwLr + jwLR)
s/e = jwLR/(Rr.(1-w²LC) + jwL(r+R))
s/e = wLR/(-j.R.r.(1-w²LC) + wL(r+R))
s/e = wLR/(wL(r+R) + j.R.r.(w²LC-1))
-----
Sauf distraction. 
salut !
merci pour vos réponses
J-P je trouve comme toi mais mon prof a du encore simplifier le truc parce qu'il trouve
H= 1 /[1+r/R+j(rCw-r/(Lw))]
je ne sais pas trop comment il a fait
merci
C'est pareil.
s/e = wLR/(wL(r+R) + j.R.r.(w²LC-1))
s/e = 1/((r+R)/R + j.r.(w²LC-1)/(wL))
s/e = 1/(1 + r/R + j.r.(wC-1/(wL)))
s/e = 1/(1 + r/R + j.(rwC-r/(wL)))



