Niveau licence

Asservissement (2)

Posté par
pascaloup6 02-04-17 à 13:01

Bonjours je suis bloqué sur un raisonnement.
Merci à ceux qui voudront résoudre et m'aidé dans mes démarches.

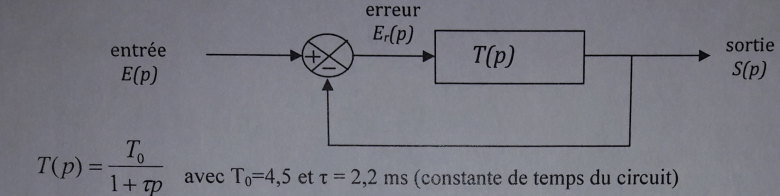
Voici le sujet :

1) Calculer la transmittance en boucle fermée Tbf(p) et la mettre sous la forme de Tbf(p)=[(Tbfo)/(1+bf.p)]
2) Exprimer Tbfo et bfCalculer les valeurs de Tbfo et bf
3) Que peut-on en conclure sur la rapidité du système bouclé ?

Pour information Tbf/o = la transmittance en boucle fermée/ouverte

Mes réponses :
1) S(p)=T(p)Er(p)
Er(p)=E(p)-S(p)
Soit S(p)=T(p)E(p)-S(p)
S(p)=[(T(p)E(p))/(2)]
J'obtiens Tbf(p)=S(p)/E(p) = Tp/2

Et là j'arrive pas à voir comment là mettre sous la forme de l'énoncé

Asservissement (2)

Posté par re : Asservissement (2) 02-04-17 à 17:53

Bonjour
Je ne suis pas un spécialiste de ce type de raisonnement mais je peut t'aider un peu quand même... Comme tu l'as écrit :

$S(p)=T(p).Er(p)=T(p).\left(E(p)-S(p)\right)$
En regroupant les termes dépendant de S(p) :

$S(p)+T(p).S(p)=T(p).E(p)$
D'où la transmitance :

$Tbf(p)=\frac{S(p)}{E(p)}=\frac{T(p)}{1+T(p)}=\frac{\frac{T_{0}}{1+\tau.p}}{1+\frac{T_{0}}{1+\tau.p}}$

$Tbf(p)=\frac{T_{0}}{1+T_{0}+\tau.p}$
En divisant tous les termes par (1+To), on obtient :

$\boxed{Tbf(p)=\frac{\frac{T_{0}}{1+T_{0}}}{1+\frac{\tau}{1+T_{0}}\cdot p}}$

Posté par re : Asservissement (2) 02-04-17 à 23:34

Je vois bien votre méthode de raisonnement mais il y aurai t-il pas un problème à ce niveau

Citation :

S(p)=T(p).Er(p)=T(p).(E(p)-S(p))
En regroupant les termes dépendant de S(p) :
S(p)+T(p).S(p)=T(p).E(p)

J'arrive pas à voir comment vous avez fait pour mettre T(p) de l'autre coté : S(p)+T(p).S(p)=T(p).E(p)

Posté par re : Asservissement (2) 03-04-17 à 11:31

Mettre S(p) en facteur à gauche puis diviser à droite et à gauche par (1+T(p) )...
Je sais que le niveau en math a beaucoup baissé mais quand même !

Posté par re : Asservissement (2) 04-04-17 à 10:09

Du coup, pour la suite, j'ai $Tbf(p) = \frac{\frac{To}{1+To}}{1+\frac{\tau }{1+To}\times p}$
Après comme c'est une boucle fermée p vaut 1 ???
$Tbf(p) = \frac{\frac{4,5}{1+4,5}}{1+\frac{\2,2\times 10^{-3} }{1+4,5}\times 1}$

Posté par re : Asservissement (2) 04-04-17 à 15:23

Citation :
Après comme c'est une boucle fermée p vaut 1 ?

J'ai bien peur que tu n'ais pas compris le sens de "p" dans ce contexte, ce qui est pourtant le minimum à savoir...
Il faut vraiment que tu revois ton cours avant de chercher à faire des exercices si tu veux vraiment comprendre quelque chose...
Telle que je t'ai écrit l'expression de Tbf(p) tu n'as plus qu'à identifier avec l'expression proposée par l'énoncé...
Tu vas obtenir une nouvelle constante de temps 5,5 fois plus petite que

, ce qui devrais t'aider à répondre à la question 3)...

Posté par re : Asservissement (2) 05-04-17 à 12:32

Excusez-moi j'ai cherché dans mes cours mais d'après ce que j'ai vu, p c'est un opérateur de Laplace (p=jw), après j'ai plus rien parce que mon professeur il a peine commencé le cour et il nous dit de faire des exos pour s'exercer.
Y a t-il quelqu'un qui peut plus me diriger sur les asservissements ?

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Asservissement (2)

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique