Inscription / Connexion Nouveau Sujet
Aspect ondulatoire de la matière
Salut à tous et à toutes, 
J'ai un exercice en physique qui me pose problème !
Voici l'énoncé :
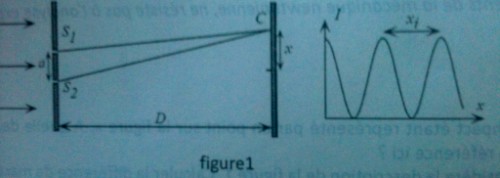
L'expérience fondamentale qui prouve le comportement ondulatoire des particules, prévu par Louis de Broglie en 1923, date de 1927. Elle est due `a Davisson et Germer, qui mirent en évidence la diffraction d'un faisceau d'´électrons par un cristal de nickel. Pour analyser les phénomènes quantiques fondamentaux que cette expérience met en relief, nous nous référerons d'abord `a une expérience plus simple conceptuellement, mais plus délicate a réaliser : les interférences d'un faisceau de particules dans un dispositif de fentes d'Young. On considère tout d'abord une onde monochromatique (longueur d'onde  ) qui arrive en incidence normale sur deux fentes d'Young distante de a. On place un écran à la distance D. On fait l'hypothèse D>>a et D>>x (image 2)
) qui arrive en incidence normale sur deux fentes d'Young distante de a. On place un écran à la distance D. On fait l'hypothèse D>>a et D>>x (image 2)
1) « un impact étant représenté par un point sur la figure ». A quelle description de la matière fait-on référence ici ? (voir image 1)
2) On considère la description de la figure 1. Calculer la différence de marche  =S2C - S1C entre les deux ondes issues des deux fentes.
=S2C - S1C entre les deux ondes issues des deux fentes.
********************************************************
1) Ici on fait référence au comportement ondulatoire de la matière.
2) Pour cette question, je suis bloqué… Je ne vois pas comment on pourrait trouvé la différence de marche alors qu'on a aucunes données chiffrées.
J'ai supposé  = (a
= (a x)/D
x)/D
Mais sans certitudes ...
Merci d'avance 
INFO : La première image est le résultat d'un expérience d'interférence avec des atomes de néons dans un dispositif de fente d'Young

Salut,
Pour la question 2 :
La différence de marche est par définition d = n (S1C-S2C) .
Tout le système est plongé dans le même milieu d'indice n.
On supposera D >> a soit S1C + S2C voisin de 2 D : S1C + S2C = 2 D (approximation)
S1C²=D²+(x-0,5 a)²
S2C²=D²+(x+0,5 a)²
S2C² -S1C² = (x+0,5 a)²-(x-0,5 a)²
(S2C-S1C)(S1C+S2C) = 2 a x <=> (S2C-S1C) 2 D = 2 a x
donc S2C-S1C est voisin de a x /D
d = n a x /D
et pour l'air n = 1 (environ)
donc en approximation :
d = a x /D
Je ne sais pas si la démonstration est au programme de terminale S ...
Merci pour ton aide gbm 
Pour la question 2 du coup je trouve :
Je ne sais pas si je dois encore simplifier ce résultat en calculant pour un maximum d'amplitude et un minimum d'amplitude ?
Au fait je ne suis pas en terminale S je suis en PCSI
ça marche, c'est ton profil qui m'avait induit en erreur
 .
.Pour la question 4 :
Lorsque l'on a une interférence constructive, l'amplitude est maximale. On a donc
Donc
Et donc
Il y a donc une frange brillante pour :
on a
Doncla distance entre deux franges brillantes, appelée interfrange vaut
Merci encore pour ton aide 
Je ne sais pas si tu as remarqué, mais ton énoncé est incomplet.
Tu n'as posté que les questions 1 et 2 ...

Petit bug au message précédent (***Edit gbm : message précédent supprimé***).
Ah oui mince je n'avais pas remarqué 
3) Que vaut le déphasage entre ces deux ondes ?
4) A partir des conditions d'interférences constructives, en déduire l'interfrange (distance entre deux maxima d'intensité)
Pour cette question j'ai écris la réponse plus haut
Question 3 :
précise ce qu'est "k" car on n'a pas forcément les mêmes notations.
Sinon, c'est correct.
Question 4.
La valeur de l'interfrange est correcte.

k correspond au vecteur d'onde à la question 3.
A la question 4, il représente simplement un entier naturel.
Merci encore pour ton aide 
Voici la suite de l'exercice (si tu veux encore m'aider  )
)
Le principe et le résultat d'une expérience d'interférences effectuée avec des atomes dans un dispositif de fentes d'Young est représenté sur la figure 2. Un nuage de quelques millions d'atomes de néon est d'abord capturé et refroidi au milliKelvin dans un piège laser. Il est ensuite lâché, sans vitesse initiale, à 3,5 cm au-dessus d'un écran percé de deux fentes parallèles, de largeur 2 microns et séparées par 6 microns. Les atomes sont détectés lorsqu'ils frappent une plaque située 85 cm sous le plan des deux fentes. La plaque détectrice enregistre l'impact de chaque atome, un impact étant représenté par un point sur la figure. On observe que ces impacts se distribuent suivant un système de franges parfaitement semblable à celui obtenu dans des interférences lumineuses ou acoustiques. Il y a des zones sombres (beaucoup d'impacts ; flux d'atome intense) parallèles à la direction des fentes, qui alternent avec des zones claires (peu ou pas d'impacts ; flux d'atomes faible).
Le contenu physique des expériences d'interférence de particules, atomes ou électrons, est beaucoup plus riche qu'un phénomène ondulatoire habituel. En lui-même, le résultat est extraordinaire parce que les atomes sont des corpuscules ponctuels dans cette expérience. Leur dimension est de l'ordre d'une fraction de nanomètre, donc très inférieure à toutes les échelles de longueur du problème considéré, distance des fentes a, ou interfrange xi. A l'inverse, une onde emplit tout l'espace ! Une onde électromagnétique, par exemple, est constituée par l'ensemble des valeurs des champs en tous les points de l'espace.
La figure 2 se trouve sur le lien ci-dessous à la page 7 :
http://www.phys.ens.fr/~dalibard/Notes_de_cours/magistere_coherence.pdf
5) On considère à présent la figure 2. Quelle observation permet d'extraire des éléments de comparaison avec la figure 1. Que peut-on en déduire sur le caractère de la matière?
6) En utilisant le résultat de la question 4, déterminer alors la longueur d'onde des atomes au niveau des fentes et leur vitesse.
5) On observe une figure d'interference tout comme dans la figure 1.
Dans la figure 1, on avait une alternance entre une zone de maximum d'amplitude (intensité lumineuse maximale) et de minimum d'amplitude (intensité lumineuse minimale) ; tandis que dans la figure 2, on a une alternance entre une zone sombre (beaucoup d'impact) et une zone claire (peu ou pas d'impact)
On peut donc dire que la matière a un comportement ondulatoire.
Après je ne sais pas comment expliquer le fait que les atomes puisse former une figure d'interférence...
Merci d'avance 


