Inscription / Connexion Nouveau Sujet
AOP intégrateur
Bonsoir,cet exercice me donne du fil a retordre donc si quelqu'un pouvais m'éclairer ça serai sympa:
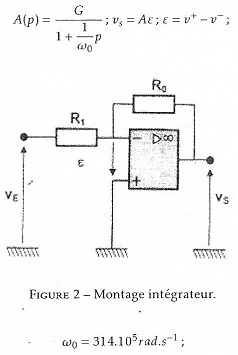
Soit un montage électronique à AOP tel que :
;
1)Exprimer la fonction de transfert H(p)=Vs(p)/Ve(p).
2)En considérant les éléments complémentaire R0=R1=10 kilos ohms,quelles modifications pouvez vous apporter à l'expression de H(p)?
3)Exprimer le gain et la phase de H(p) au sens de Bode sous forme simplifiée.
4)Quelle fonction rempli ce montage?
Et voici mes réponses:
Le 1) j'ai pas trouvé,j'ai trouvé le gain mais pas H(p).
3) Au début j'utilisais Millman en disant:
Et
Mais j'ai relu le cours et j'ai vu que ce montage est un montage inverseur vu que le moins est en haut,et l'énoncé nous dit que c'est aussi un intégrateur.
Bref,en gros j'ai vu sur wiki qu'en appliquant le théorème de supperposition sur ce type de montage on a:
.(il faut que je revois ce théorème pour voir d'ou vient la partie avec Ve).
Avec Vs=A.(V+-V^- ) et comme V+=0,alors V-=
Puis on factorise par Vs et on a
On a donc:
Le gain c'est le
2)Si R1=R0 alors .
4)Ce montage est un montage intégrateur (et inverseur)La sortie est proportionnelle à l'intégrale temporelle de la tension d'entrée.
Bonjour
Au début j'utilisais Millman en disant:...
Excellente méthode à condition de l'appliquer correctement :
Remarque un peu hors sujet mais susceptible de t'aider à reprendre tes marques : supposer l'ampli op idéal revient à faire tendre A vers l'infini : tu obtiens bien alors un ampli inverseur comme étudié les années passées.
Ici : il faut poser :
Je te laisse continuer en espérant t'avoir remis sur les bons rails.
PS : en aidant un peu certains étudiants en électromagnétisme, il me semble avoir trouvé dans cette discipline pire que tes professeurs de l'an passé dans cette discipline

Je trouve
H(p) = -(R0/R1)/(1 + p * (R0+R1)/(R1.wo.G))
Et avec Ro=R1 -->
H(p) = - 1/(1 + p * 2/(wo.G))
C'est un filtre passe bas du 1er ordre , la pulsation de coupure étant ...
Sauf distraction. 
La force de l'habitude... Jean469 a sûrement compris que le R2 de mon message correspond en fait au Ro du schéma...


