Un ampli apérationnel a 2 entrées, l'une notée V+ et l'autre notée V- (par exemple)

Il a aussi une sortie (par exemple notée s)

Epsilon est la différence de potentiel entre les 2 entrées : = V+ - V-

On a la relation : s = A * epsilon (avec A, le gain "interne" de l'ampli opérationnel).

En première approximation (et souvent suffisante), A est un réel positif de très grande valeur numérique.

Comme s (la tension de sortie) ne varie que de quelques volts au maximum (par exemple s peut varier entre -10 V et + 10 V), on a epsilon = s/A avec A très grand.

Donc, pour la plupart des calculs on a (attention, pas = 0 mais quasi égal à 0). Ceci reste vrai si l'ampli travaille dans sa zone linéaire ... et donc par exemple pas comme comparateur.

Les amplis opérationnels, ont de très grandes impédances d'entrée , si bien que les courants pénétrant (ou sortant) de l'ampli par les pin d'entrée (V+ et V-) sont très petits.

En première (et souvent suffisante) approximation, on peut considérer dans les calculs que ces courants sont nuls (bien que ce ne soit que "quasi" nul)
-----

Cas d'un montage inverseur :



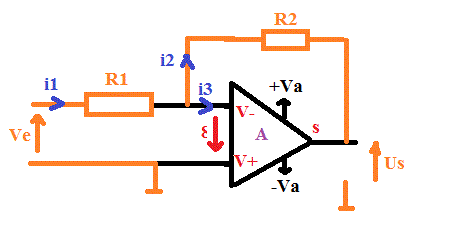
On écrit l'équation de la maille d'entrée : Ue - R1.i1 + = 0

Mais on sait que et donc on a pratiquement : Ue - R1.i1   0 (1)

Equation du noeud de courant : i1 = i2 + i3

Mais on sait que i3 est quasi nul (grâce à l'énorme impédance d'entrée de l'ampli Op) et donc, en première (et souvent suffisante) approximation, on a : i1 i2 (2)

On écrit l'équation d'une autre maille (suivre sur le dessin) : Us + R2.i2 + = 0  

Et comme on sait que , on a : Us + R2.i2 (3)

On a donc le système (1), (2) et (3) :

Ue - R1.i1 0
i1 i2
Us + R2.i2

Qui donne :
Ue R1.i1
Us - R2.i1

et donc Us/Ue - R2/R1
-----
Sauf distraction.