Inscription / Connexion Nouveau Sujet
Anneaux de maxwell
Bonjour,
Le projet que je dois étudier est le mouvement du yoyo
j'ai mesuré les données suivantes , le yoyo est d'une masse de 0,5 kg et de grand rayon 5cm,il est traversé d'une tige de 2,5mm de rayon sur lequel est attachée une corde, cette même corde est attaché sur un trépied et mesures 37,5cm
je dois trouver le temps que le yoyo mets pour descendre ainsi que sa position
j'ai déjà calculer l'accélération du centre de gravité = - 9.4 m/s^2
j'ai aussi calculer la tension de la corde = 0,21 N
ainsi que le moment d'inertie =0.000006 kg m^2
Bonjour
A priori, l'expression de l'accélération du centre d'inertie du yoyo dans un repère terrestre est donnée par la relation :
Ta description du yoyo me semble imprécise : il vaudrait mieux le considérer comme un ensemble de 3 cylindres coaxiaux : 2 identiques de rayon 5cm et un de rayon 2,5cm et il faudrait un moyen de déterminer la répartition de masse entre ces trois cylindres...
A priori, ta valeur absolue de a me parait bien trop proche de g...
je suis d'accord avec la relation c'est ce que j'ai trouvé mais ce qui me gêne c'est le signe de g si je mets g négatif j'ai la tension de la corde qui devient négative
et je n'ai pas compris pourquoi séparer le yoyo en plusieurs parties
Négliger la masse de la partie centrale revient à calculer le moment d'inertie comme celui d'un cylindre de masse m=0,5kg et de rayon R=5cm.
On obtient ainsi une valeur approchée du moment d'inertie par rapport à l'axe de symétrie du yoyo :
Il ne s'agit que d'un ordre de grandeur mais il permet d'affirmer que la valeur réelle n'est sûrement pas 6.10-6kg.m2...
et je n'ai pas compris pourquoi séparer le yoyo en plusieurs parties
Essentiellement pour obtenir une valeur précise de J.
Cela dit, "à la louche", je pense cette valeur proche de 6.10-4kg.m2, ce qui conduit à une accélération du centre d'inertie du yoyo d'environ 0,051m/s2;
Je trouve la valeur de r bien petite devant R... Dans ce cas, au dénominateur de l'expression de l'accélération, le terme prépondérant est J/r2...
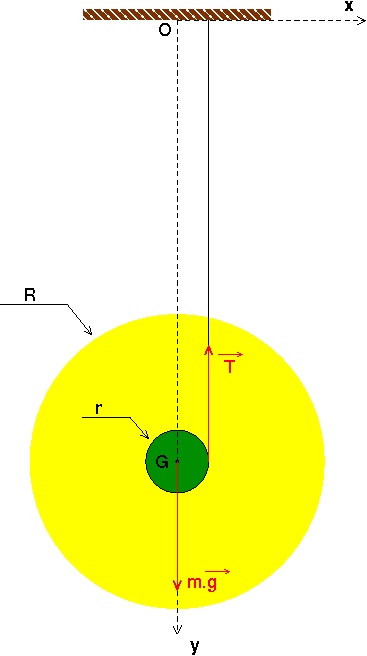
Le vecteur accélération lors de la descente est orienté vers le bas (sens et direction du vecteur g)
Si tu orientes ton axe vertical vers le bas, tu obtiens un vecteur accélération dont la composante sur cet axe est positive. La tension du fil est évidemment orientée vers le haut.
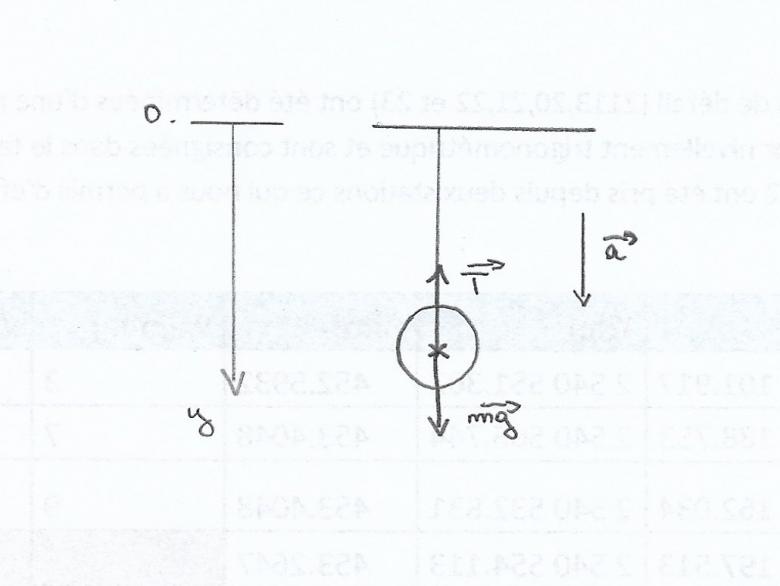
Aide-toi d'un schéma propre avec une représentation correcte des vecteurs forces. Si tu veux, tu peux le scanner et le poster sur le forum.
Je te laisse réfléchir à tout cela et poster quelque chose de propre...
Je ne vois pas trop comment, avec un tel schéma, tu peux obtenir l'accélération de G dans le repère terrestre (O,x,y)... Je ne suis pas sûr que tu ais vraiment compris...
La tension du fil et la trajectoire de G sont deux verticales décalées de r, le rayon de la tige centrale. C'est d'ailleurs ce rayon qui intervient dans l'expression de l'accélération et non R, le rayon du yoyo...