Inscription / Connexion Nouveau Sujet
Analyseur de spectre analogique
Bonjour, j'aimerais qu'on m'apporte de l'aide sur un exercice de traitement du signal.
On dispose d'un circuit RLC série classique avec tension de sortie aux bornes de R et capacité du condensateur variable.
1. Mettre la fonction de transfert sous la forme canonique.
H=1A/1+jQ(w/w0-w0/w)
Ici pas de souci par pont diviseur de tension puis identification je trouve A=1 Q=1/R*
L/C et w0=1/(LC)
Nature du filtre: je fais une analyse asymptotique je trouve que c'est un passe bande.
2. Comment varie Q avec R : inversement proportionnels
Expression de la bande passante: 
w=w0/Q=R/L
Comment évoluent 
w et w0 avec C: w independant de C et w0 inversement proportionnelle à C.
3) On utilise le montage en tant qu'analyseur de Fourier analogique.
On met à l'entrée de ce circuit le signal ve(t) signal carré de fréquence f=1/T=3.0kHz
Et E=10V.
On a la décomposition en série de Fourier:
ve(t)=E/2+2E/
*
1/(2n-1)*sin(2f(2n-1)t))
Somme de 1 à l'infini.
a) Déterminer le signal de sortie vs(t) si f0=3.0kHz et Q=20.
Je calcule la bande passante qui vaut 150 Hz donc seul le foncdamental est réstitué car filtre passe bande.
vs(t)=2E/*sin(2ft)
b) On me demande comment pourrait on utiliser le circuit pour déterminer le spectre en fréquence de ve(t) et quelle serait alors la précision en fréquence obtenue dans le spectre.
J'ai pensé à augmenter la bande passante en diminuant Q le facteur de qualité pour que les harmoniques soient restitué.
Je vois pas trop comment terminer.
Merci de votre aide.
Bonsoir
Je trouve que tu as globalement bien travaillé !
Pour la 2a) , comme tu l'as très bien dit : la fréquence du premier harmonique est effectivement hors de la bande passante. Tu pourrais peut-être en rajouter un peu en calculant la valeur du module de H à la fréquence 3fo.
Pour la dernière question, la clé se trouves dans l'énoncé : "capacité du condensateur variable. " (j'aurais personnellement écrit "capacité réglable" ou "capacité ajustable" car l'adjectif "variable" sous-entend fréquemment une variation en fonction du temps... mais c'est un détail !)
Il suffit de remplacer le condensateur par un autre de capacité fois plus faible de façon que la fréquence propre du filtre devienne 3fo : l'amplitude du signal de sortie obtenue sera l'amplitude du premier harmonique. En remplaçant le condensateur initial par un autre de capacité
fois plus faible, ton filtre sélectionnera l'harmonique de fréquence 5fo et ainsi de suite...
Bonsoir
En répondant trop vite à ton message j'ai commis une grosse etourderie. Sachant que la fréquence propre du filtre est inversement proportionnelle à la racine carrée de C, multiplier la fréquence propre du filtre par 3 s'obtient en divisant C par 9 et non par 3... Multiplier la fréquence propre du filtre par 5 s'obtient en divisant C par 25. Toutes mes excuses!
Bonsoir vanoise, j'ai bien compris ton explication, merci pour ta réponse rapide et constructive.
Bonne soirée.
Bonjour
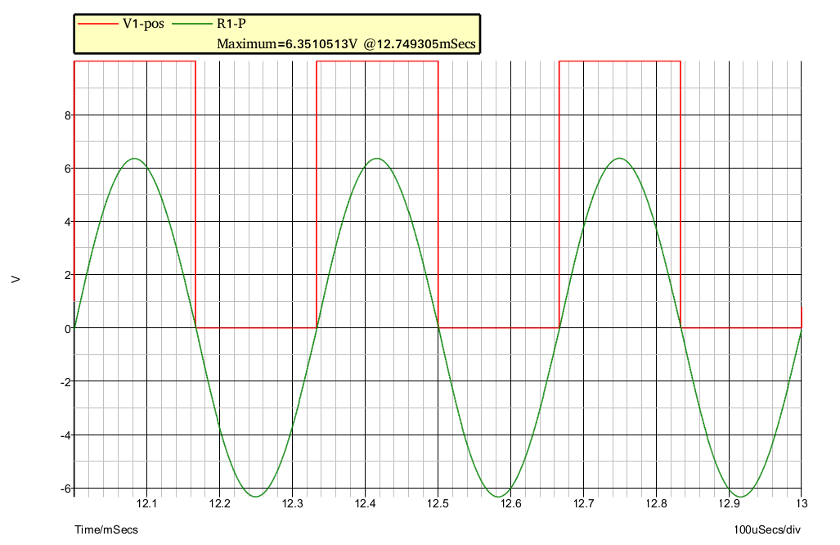
Je ne sais pas si tu as beaucoup de temps à consacrer à ce type d'exercice... Pour illuster les propos précédents. Voici, en vert, les courbes correspondant à la tension de sortie du filtre quand :
1er cas : sa fréquence propre est la fréquence de la tension d'entrée fo ; tu peux vérifier que cette tension de sortie correspond bien à l'expression théorique du fondamental de la tension d'entrée ; Le filtre est donc bien suffisamment sélectif pour éliminer de façon quasi totale la composante continue et les harmoniques.
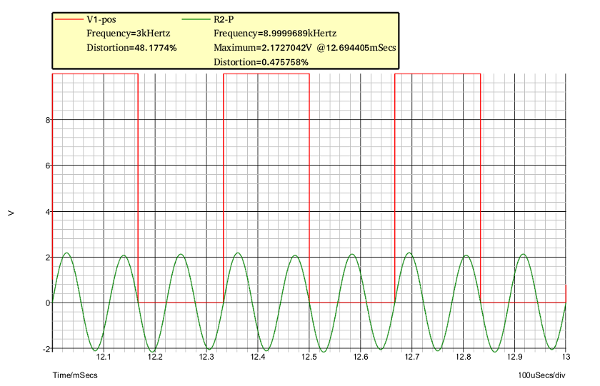
2ème cas : sa fréquence propre vaut 3fo : tu peux constater que la tension de sortie correspond bien à l'expression théorique du premier harmonique ;
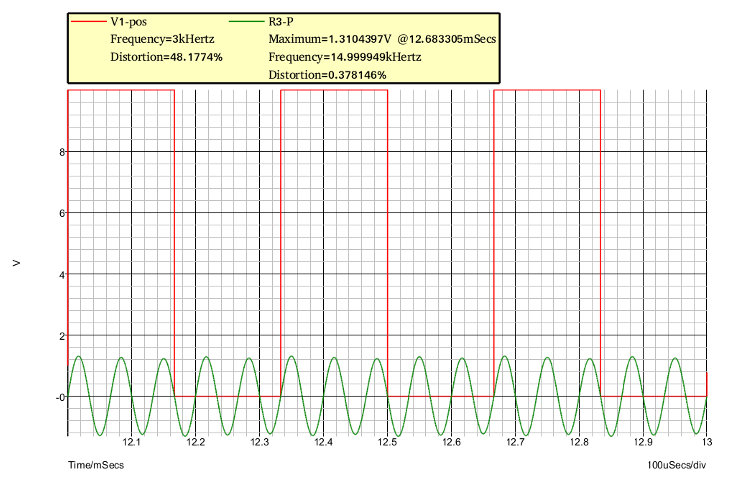
3ème cas : sa fréquence propre vaut 5fo : tu peux constater que la tension de sortie correspond bien à l'expression théorique du deuxième harmonique ;
Remarque : conformément à l'énoncé, j'ai fait varier la fréquence propre en modifiant la valeur de C mais cela modifie aussi la valeur de Q qui est ainsi multiplié par 3 dans le deuxième cas et par 5 dans le troisième. Cela explique pourquoi le taux de distorsion du signal de sortie diminue légèrement tout en restant toujours très faible, ce qui est la preuve que le signal de sortie peut être considéré comme quasi sinusoïdal.
Bonsoir
pour la question 3b) comment s y prendre?
J'ai partiellement répondu dans mon message du 29-09-16 à 15:18, simulations informatiques à l'appuis.
Il faut réaliser le montage en utilisant des "boîtes" de résistances étalon et des "boîtes" de condensateurs étalon de façon à faire varier la fréquence propre du filtre passe bande tout en maintenant un facteur Q très élevé de façon à avoir une bande passante très étroite.
En augmentant très progressivement la fréquence propre de celui-ci, on remarque que la tension de sortie passe pour la première fois par un maximum pour une fréquence propre du filtre qui représente la fréquence fo du signal. Si on continue à augmenter la fréquence propre du filtre, on obtient un autre maximum de la tension de sortie pour une fréquence égale à 3 fois la fréquence du signal, l'amplitude de la tension étant 3 fois moins grande que pour le premier maximum. Si on continue à augmenter la fréquence propre du filtre, on obtient un autre maximum d'amplitude pour une fréquence propre du filtre égale à 5 fois celle du signal, cette amplitude étant 5 fois plus faible que la première...
Bref : on peut ainsi montrer que les harmoniques correspondent à des fréquences multiples impairs de la fréquence fondamentale et que les amplitudes des harmoniques sont inversement proportionnelles au rang des harmoniques...
Pour la précision des mesures, elle dépend de la précision avec laquelle sont connues les capacités des condensateurs et les résistances...
Annuler
connectez vous