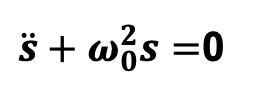je crois que l'image ne s'est pas attachée, la voici

Bonjour
Ce n'est pas tout à fait cela.Tu as une équation horaire faisant intervenir deux inconnues : s_o et .
Il te faut donc deux équations. La première concerne l'élongation initiale :
s₍₀₎=s_o.cos()
La deuxième va faire intervenir la vitesse initiale. Il faut commencer par dériver s(t) par rapport à t pour avoir l'expression générale de la vitesse en fonction du temps puis s'intéresser au cas particulier de l'instant initial.

Merci pour votre réponse.

Si je dérive s(t) qui est donc égal à v je trouve :
s(t)' = v(t) =  -ω0sin(ω0*t)
soit à t = 0, v(0) = 0 ? je pense que je me trompe car ça contredit la donnée dans l'énoncé.
Hormis cela je ne comprend pas pourquoi exprimer la vitesse m'aidera à résoudre ce problème, est ce que vous pouvez m'éclairer ?

Merci d'avance !

Pourquoi poser a priori =0 ?
Relis mon précédent message...

Mais si on utilise l'expression s(0)= s0.cos(ϕ) on trouve cos(ϕ) = 1 soit ϕ = 0 non ?

En exprimant les distances en centimètres, cela donne :
1= s_o.cos()
Cela donne une seule équation pour deux inconnues : s_o et . Il faut donc une seconde équation ; elle s'obtient en s'intéressant à la vitesse initiale comme déjà expliqué.
Ce n'est pas un hasard si l'énoncé fournit à la fois l'élongation et la vitesse initiales.

Si j'utilise une autre relation j'ai
s(t) = v0/ω sin(ωt)
donc s0 = 1/1 et je retrouve le même résultat

Tu ne confondrais pas par hasard l'amplitude s_o et l'élongation à la date t=0 notée s₍₀₎ ? Pour éviter ce genre de confusion,de nombreux énoncés notent l'amplitude s_m ou s_max.

je pense que vous avez raison..
donc si je reprends s(t)' = v(t) =  -ω0sin(ω0*t + ϕ )
à t = 0, v0 = 1 = -sin(ϕ ) donc sin(ϕ ) = -1 et ϕ = 3π/2 c'est bien ça ?

Tu as oublié s_o dans l'expression de la vitesse.

ah oui donc v(t) =  -s0*ω0sin(ω0*t + ϕ )
v0 = 1 = -s0*sin(ϕ) donc s0 = -1/sin(ϕ)
soit s(0) = -1/sin(ϕ) * cos(ϕ)
je ne vois pas où je peux réutiliser cette expression

Tu avances mais avec quelques maladresses. Je résume en continuant à exprimer les distances en centimètres. Les deux relations déjà obtenues sont :
(1) : 1=s_o.cos()
(2) : -1=s_o.sin()
L'amplitude étant, par définition, une grandeur strictement positive, on en déduit d'abord :
cos()>0 et sin()<0
Aides-toi éventuellement d'un cercle trigonométrique ; ces deux inégalités impliquent une inégalité vérifiée par .
Pour être ensuite plus précis : la "division membre à membre" des deux égalités conduit à :
tan()=-1
En tenant compte aussi des inégalités, cela suffit à définir de façon précise (modulo 2 bien sûr).
Facile ensuite d'obtenir s_o.

Si je reprends donc cos(ϕ)/sin(ϕ) = tan(ϕ) = -1
tan (π/4) = 1 soit ϕ = -π/4
s(0)=s0.cos(ϕ)
s0 = s(0)/cos(ϕ) = 1/cos(-π/4) = 1/(1/√2) = √2
Est-ce que c'est correct ?
    

Attention à la rigueur de la rédaction et à la trigonométrie.

et non l'inverse ! coup de chance : cela donne tout de même (-1) !

Cela conduit à deux solutions possibles (modulo 2) : -/4 et 3/4 ; c'est parce que le cosinus est positif et le sinus négatif, qu'il faut retenir la valeur -/4 rad.

Deux remarques concernant s_o :

1° : un résultat présenté sans unité, lorsque l'unité existe comme ici, est considéré comme faux par la plupart des correcteurs d'examens et de concours ;

2° : jamais un appareil de mesure ne fournit l'indication . Suivant sa précision, il pourra indiquer 1,4cm, 1,41cm, voire 1,414cm ; bref : toujours indiquer un résultat sous forme de nombre décimal avec un nombre de chiffres significatifs dépendant de la précision des données ; le plus souvent : 3. Donc ici :

oulalah oui j'ai inversé cos et sin n'importe quoi merci pour votre remarque et vos conseils (étant donné qu'on travaille sous forme de qcm et que la calculatrice est interdite je ne peux pas fournir de résultats sous forme de nombre décimal)
Merci pour votre aide !