Inscription / Connexion Nouveau Sujet
amplificateur opérationnel
Bonsoir,
j'ai un exercice avec cet AO, on me demande de calculer le facteur d'amplification A et je trouve que A= 2, est-ce juste ? si non pouvez vous m'aider
Ensuite on me de demande de calculer ie en fonction de R et Ue et la je n'y arrive pas, déplus je dois en déduire la valeur de la résistance d'entre du filtre.
Merci pour votre aide
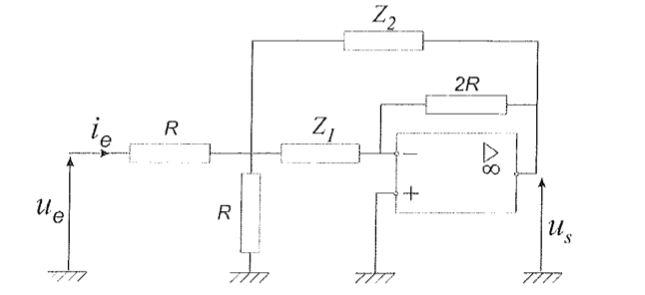
Comment peux-tu trouver A = 2 sans connâitre Z1 et Z2.
De plus, on devrait avoir un signe - dans l'expression de A avec un tel montage.
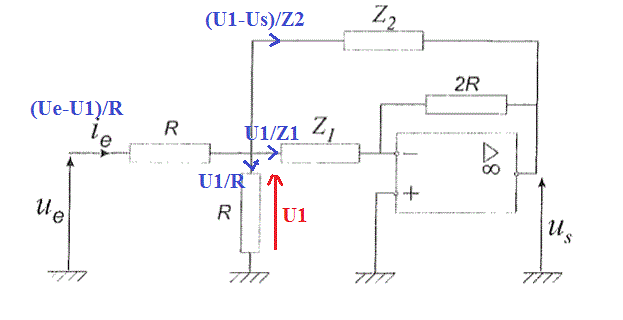
Loi des noeuds:
(Ue-U1)/R = U1/R + U1/Z1 + (U1-Us)/Z2
Ue/R = U1(2/R + 1/Z1 + 1/Z2) - Us/Z2 (1)
---
Us = -U1.(2R/Z1)
U1 = - Z1 . Us/(2R) (2)
---
Eliminer U1 entre (1) et (2) et tu pourras trouver Us/Ue = ...
Sans garantie, on arrive à Us/Ue = -2R.Z2/(2Z1Z2 + RZ2 + RZ1 + 2R²)
Que je n'ai pas vérifié ...
-----

À oui j ai oublié des dire , ce que j' ai donné est une partie de exercice et ici les Z sont des résistances R
Moi je pensais utiliser millman , ca serait beaucoup plus simple mais je n y arrive pas, sachant que Z1 et Z2 sont égales à R
En repartant de ma réponse générale précédente :
Us/Ue = -2R.Z2/(2Z1Z2 + RZ2 + RZ1 + 2R²)
Si Z1 = Z2 = R, alors :
Us/Ue = -2R²/(2R² + R² + R² + 2R²)
Us/Ue = -2/6
Us/Ue = -1/3
---------------------------------
En refaisant tout depuis le début avec Z1 = Z2 = R
Loi des noeuds:
(Ue-U1)/R = U1/R + U1/Z1 + (U1-Us)/Z2
Ue/R = U1(2/R + 1/Z1 + 1/Z2) - Us/Z2
Ue/R = U1(2/R + 1/R + 1/R) - Us/R
Ue = 4.U1 - Us (1)
---
Us = -U1.(2R/Z1)
Us = -2.U1 (2)
---
(1) et (2) --->
Ue = 4.(Us/-2) - Us
Ue = -3 Us
Us/Ue = -1/3
--------------------
Pour ie (avec Z1 = Z2 = R)
U1 = - Z1 . Us/(2R)
U1 = - Us/2
Us/Ue = -1/3
U1 = -(-(1/3).Ue/2) = Ue/6
ie = (Ue-U1)/R
ie = (Ue - Ue/6)/R
ie = 5Ue/(6R)
-----
Sans vérification. 
dans la suite de mon problème on doit trouver la résistance d'entre Re ça je n'y arrive pas non plus . Ensuite, si on prendra Z1=Z2 des condensateurs de capacités 200 nF, je dois déterminer fr (fréquence de la résonance) ainsi que Q, mais de nouveau je bloque.... ça fais des heures que je tourne en rond  , pouvez vous m'aider svp
, pouvez vous m'aider svp 
Si Z1 = Z2 = R :
Re = Ue/ie
Re = 6R/5
-----
Z1=Z2 des condensateurs de capacités 200 nF ... Et R = ????
Z1=Z2= -j/(wC)
Us/Ue = -2R.Z2/(2Z1Z2 + RZ2 + RZ1 + 2R²)
Us/Ue = 2R/(wC)/(-2/(w²C²) - jR/(WC) - jR/(WC) + 2R²)
Us/Ue = R/(wC)/(-1/(w²C²) - jR/(WC) + R²)
Us/Ue = -wRC/(1 - w²R²C² + jwRC)
...
-----
Vérifie. 
Si tu ne n'essaies rien par toi même ...
Q = fo/(Delta f)
Avec fo la fréquence "centrale" et Delta f la bande passante du filtre pour un gain de -3dB (donce atténuation d'un facteur 1/V2)
Us/Ue = -wRC/(1 - w²R²C² + jwRC)
|Us/Ue| = wRC/V[(1-w²R²C²)²+w²R²C²]
Resonnance pour 1-w²R²C² = 0 ---> Wo = 1/(RC), fo = 1/(2Pi.RC)
A la résonnance, |Us/Ue| = 1
Bande passante:
wRC/V[(1-w²R²C²)²+w²R²C²] = 1/V2
2w²R²C² = (1-w²R²C²)²+w²R²C²
w²R²C² = (1-w²R²C²)²
(1-w²R²C²)² - w²R²C² = 0
(1 - w²R²C² - wRC)(1 - w²R²C² + wRC) = 0
Dont les sol positives sont :
w1.RC = (-1 + V5)/2 et w2.RC = (1 + V5)/2
RC.(w2 - w1) = [(1 + V5+1-V5)/2 = 1
w2-w1 = 1/(RC)
Delta f = 1/(2Pi.RC)
Q = 1
-----
fr = 1/(2Pi.RC) = 1/(2.Pi*50.10^3*200.10^-9) = 15,9 Hz
Q = 1
-----
Comme je n'ai rien relu, tu as vraiment intérêt à essayer de comprendre pour trouver les endroits où je me suis peut-etre égaré et corriger au besoin 


