Inscription / Connexion Nouveau Sujet
Amplificateur opérationnel
Bonjour 
L'amplificateur opérationnel fonctionne en régime linéaire et est supposé parfait. est une résistance ajustable et on pose
et
.
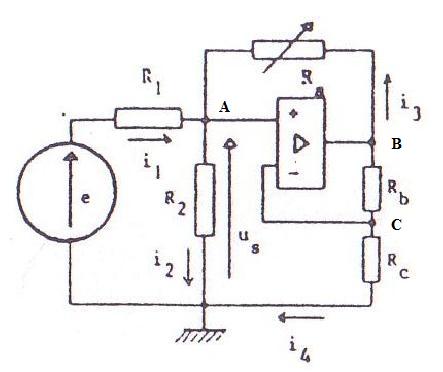
Déterminer B/A et en fonction de
.
Je cherche donc à exprimer . J'ai pensé à appliquer Millmann en A et le diviseur de tension en C mais il me manque des infos pour conclure..
Un coup de pouce ? 
Salut vieux 
J'ai pas fait les calculs, mais en appliquant millman en A tu aura une relation entre Us e et V(B)
Il faut alors trouver une relation entre V(B) et e ou Us
Donc je pense appliquer millman en B ou en C (je sais pas celui qui donne mieux les calculs ...) et en tenant compte que epsilon = 0 et V+=V(A)=V-=V(C) ...
Bonjour,
Voici ce que je propose, mais je ne sais pas si c'est juste :
Us = i2.R2
i2 = i1 + i3
i1 = (e - Us) / R1
i3 = (VB - Us) / Ra
VB = (Us - VC) . A
VC = VB.Rc / (Rb+Rc)
VB = [Us - VB.Rc / (Rb+Rc)] . A
VB = Us. A - VB.Rc / (Rb+Rc) . A
VB.[1 + A.Rc/(Rb+Rc)] = Us.A , avec 1 négligeable devant A . …
VB.A.Rc /(Rb+Rc) =~ Us.A
VB = Us.(Rb+Rc)/Rc
i3 = [Us.(Rb+Rc)/Rc - Us] / Ra
i3 = Us.(Rb+Rc)/(Ra.Rc) - Us/Ra
i3 = Us.[(Rb+Rc)/(Ra.Rc) - 1/Ra]
i3 = Us.[(Rb+Rc)/(Ra.Rc) - Rc/(Ra.Rc)]
i3 = Us.[(Rb+Rc-Rc) / (Ra.Rc)]
i3 = Us. Rb/(Ra.Rc)
i2 = (e-Us)/R1 + Us.Rb/(Ra.Rc)
i2 = (e.Ra.Rc - Us.Ra.Rc + Us.R1.Rb) / (R1.Ra.Rc)
Us = R2 . (e.Ra.Rc - Us.Ra.Rc + Us.R1.Rb) / (R1.Ra.Rc)
Us = (e.R2.Ra.Rc - Us.R2.Ra.Rc + Us.R1.R2.Rb) / (R1.Ra.Rc)
Us.(R1.Ra.Rc) = e.R2.Ra.Rc - Us.R2.Ra.Rc + Us.R1.R2.Rb
Us.(R1.Ra.Rc + R2.Ra.Rc - R1.R2.Rb) = e.R2.Ra.Rc
Us = e.R2.Ra.Rc / (R1.Ra.Rc + R2.Ra.Rc - R1.R2.Rb)
Donc Us(t) = cos(wt) . R2.Ra.Rc / (R1.Ra.Rc + R2.Ra.Rc - R1.R2.Rb) sans déphasage.
J'insiste, je ne suis pas dans ce domaine en ce moment et il est possible que je sois tombé dans un piège, même grotesque, donc méfiance par rapport à ce résultat.
Si tu as une réponse ça m'intéresse.
Bon courage.


