Inscription / Connexion Nouveau Sujet
Amplificateur opérationel différentiel
Bonjour, gros problème pour calculer une expression de la sortie d'un AO ALI dit "différentiel".
Voilà, c'est un cas très classique, (pour le schéma, voilà un lien( je ne vais pas le refaire)![]() ).
).
Voici ma démarche.
Une boucle de rétroaction  On est linéaire.
On est linéaire.
On peut donc utiliser le théorème de superposition.
De plus i+ et i- les courants d'entrée sont nul. V+ - V- = 0
Deux sources : V1 et V2.
On éteint V1 : La branche du bas disparée.
Par une loi des mailles à droite, et en faisant intrevenir un courant i :
V1=R1.i
Vs=-Rf.i
D'ou Vs=-(Rf/R1).V1
On éteint V2 : La branche du haut diparée.
Par une loi des mailles, et en faisant intrevenir un courant i :
V2=(R2 + Rg).i
Vs = -Rg.i
D'ou Vs = -(Rg/Rg+R2).V2
Et je déduit par le théorème de superposition.
Vs= -(Rf/R1).V1 -(Rg/Rg+R2).V2 .
Mais hélas, ça péche quelque part cr je ne rouve pas ce qu'il faut.
Je suis sensé trouver : (Rg(Rf+R1)/R1(R2+Rg))V2 - (Rf/R1).V1
Voilà,merci de votre aide.
@++
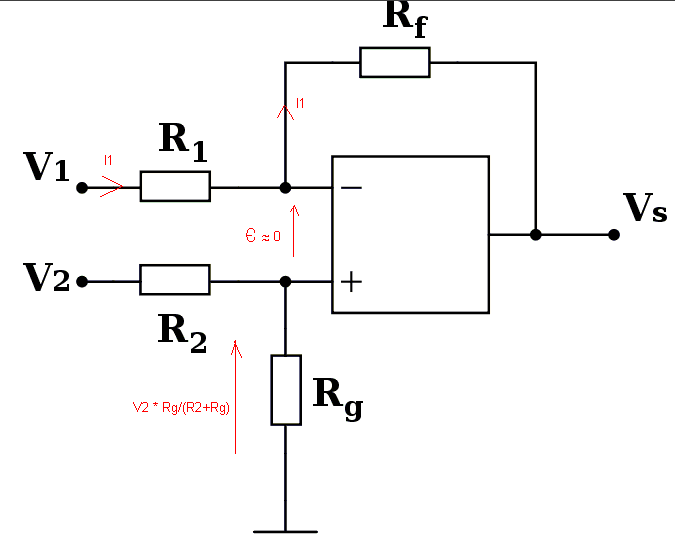
V+ = V2 * Rg/(R2 + Rg)
V+ presque égal à V- --->
V- = V2 * Rg/(R2 + Rg)
I1 = (V1 - V-)/R1
I1 = (V1 - (V2 * Rg/(R2 + Rg)))/R1
I1 = (V1.(R2 + Rg) - V2.Rg)/(R1.(R2 + Rg))
Vs = V- - Rf.I1
Vs = V2 * Rg/(R2 + Rg) - Rf.(V1.(R2 + Rg) - V2.Rg)/(R1.(R2 + Rg))
Vs = [V2.R1.Rg - Rf.V1.(R2 + Rg) + V2.Rg.Rf]/(R1.(R2 + Rg))
Vs = [V2.R1.Rg + V2.Rg.Rf]/(R1.(R2 + Rg)) - Rf.V1.(R2 + Rg)/(R1.(R2 + Rg))
Vs = V2.(R1.Rg + Rg.Rf)/(R1.(R2 + Rg)) - Rf.V1.(R2 + Rg)/(R1.(R2 + Rg))
Vs = V2.(Rg.(R1 + Rf))/(R1.(R2 + Rg)) - Rf.V1./R1
Vs = V2.(Rg.(R1 + Rf))/(R1.(R2 + Rg)) - V1.(Rf/R1)
-----

Inutile de passer par le théorème de surperposition. Un calcul direct fonctionne aussi bien.
1. Calcule le potentiel de l'entrée non-inverseuse (+) en fonction de ,
et
(diviseur de tension par exemple)
2. En utilisant le fait que la différence de potentiel entre les deux entrées d'un l'A.O. idéal est nul, détermine l'expression de la tension aux bornes de (
).
3. Remarque et
sont en série (aucun courant ne rentre dans l'entrée inverseuse) et soumis à une différence de potentiel
. Déduis-en une deuxième expression de
en fonction de
et
(diviseur de tension à nouveau). Compare-la à la précédente pour en déduire l'expression de
.
bonjour à tous.
juste une petite remarque, peut-être que c'était sous-entendu, mais dans le doute...
Une boucle de rétroaction
Encore une fois, peut-être c'était sous-entendu, mais si ça ne l'était pas, reviens à l'équation différentielle vérifiée par l'AO dans le cas d'un montage à rétroaction positive pour t'en convaincre.
nan, je ne savais pas. Pdt le cours, le prof a fait cette remaque de lien entre linéarité et boucle de rétraction, de manière oral.
je veux bien pluis d'explication avec un lien...
@+
Alors comme ça je n'ai pas trouvé de lien, mais peut-être as-tu vu en cours que la tension de sortie d'un AO vérifiait une équation de la forme :
?
pour chaque cas, il est possible de voir si la solution de cette équation converge ou non; dans le premier cas, l'AO est en régime linéaire, dans le second il part en régime saturé...
exacte, on a vu sa sous forme d'une rétraction ++ ou d'une rétraction +-. C'est schémat à l'image de se que l'on peut fire en automatique.
Je t'avoue ne pas vraiment faire le lien cette étude et les schémas de AO. Comment voir par eemple que celui que j'ai proposé est un AO linaire (boucle +-). As tu un eemple et un contre exemple ?
celui de ton exemple est forcément en régime linéaire, il n'y a qu'une seule boucle de rétroaction ET elle est négative.
Un exemple classique d'AO qui sature : le comparateur à hystérésis ( en gros, un amplificateur inverseur dont tu inverses les bornes d'entrée + et - . dans ce cas, il n'y a qu'une boucle de rétroaction positive et il sature.
Un exemple où il faut, en principe, faire une étude plus approfondie est le montage simulant la résistance négative (regarde sur le net la tête qu'il a...)
Juste pour info complémentaire.
Il est tout à fait possible de sortir du régime linéaire pour le montage proposé (et pour presque n'importe quel autre d'ailleurs)
Pour que ce montage reste en régime linéaire, il faut que :
a) La tension sur l'entrée + de l'OP reste entre les rails d'alimentation (et donc dépend de V2, R2 et Rg)
b) Il faut que la tension Vs (calculée par la formule trouvée) reste aussi entre les rails d'alimentation (et donc dépend de V1 ,V2 et des valeurs des composants passsifs (résistances)).
Ceci étant pour un ampli idéal.
En pratique, il existe souvent des tensions de déchets qui empêchent la sortie de l'OP "d'aller" jusqu'aux rails d'alimentation. Ces tensions de déchet sont parfois différentes pour les tensions vers le rail du bas de celle pour le rail du haut).
Ces tensions de déchet sont souvent aussi dépendantes du courant dans la charge (connectée sur Vs).
Donc, même un montage à rétroaction négative, peut être sorti de son régime linéaire en fonction des valeurs des tensions d'entrée et des valeurs des composants.



