Inscription / Connexion Nouveau Sujet
Amortisseur d’un siège de tracteur
Bonjour, je me permets de poster cet exercice car j'ai beaucoup de mal à le commencer. En fait, je ne suis vraiment pas sûre de moi ce qui fait que je commence beaucoup de choses sans en aller au bout et je finis par tout rayer.
J'espère que vous pourrez m'aider.
Je vous en remercie par avance.
Énoncé :
Le siège d'un tracteur est monté sur ressorts. On veut comparer le comportement du siège lorsqu'un adulte ou un enfant s'assoit dessus.
On modélise la personne assise sur le siège par un objet masse m fixé sur un ressort de constante de raideur k et longueur à vide l0.
I. Étude statique Le tracteur est immobile sur un sol horizontal. Exprimer la longueur leq du ressort à l'équilibre en fonction de m; g; k et l0. Le ressort est-il comprimé ou étiré ?
II. Étude dynamique Le tracteur est animé d'un mouvement rectiligne uniforme. On se place dans le référentiel lié au tracteur, supposé galiléen. Au cours du déplacement, le siège monte brusquement. Il y a des frottements fluides f(vecteur) = -
. Les conditions initiales sont z(t = 0) = 0 et z'(t=0)=v0.
1. Établir l'équation différentielle vérifiée par la position verticale z(t)=l-leq. La mettre sous la forme canonique
z"+ 2
z' + (
0)²z=0
en exprimant et 0.
2. On considère tout d'abord un adulte de masse m = 75,0 kg.
a) Calculer et 0.
b) Quelle est la nature du mouvement du siège (pseudo périodique, critique ou apériodique) ?
c) Déterminer la solution z(t) avec les conditions initiales z(t = 0) = 0 et z_(t = 0) = v0. Calculer le temps d'amortissement caractéristique 
=1/ et la pseudo-pulsation du mouvement.
d) Dessiner qualitativement z(t).
3. On considère un enfant de masse m = 15,0 kg.
a) Calculer et 0.
b) Quelle est la nature du mouvement du siège (pseudo périodique, critique ou apériodique) ?
c) Calculer le temps d'amortissement caractéristique =1/
4. Quel est l'intérêt pratique de la présence des amortisseurs. Celui considéré dans cet exercice est-il adapté au
poids de l'adulte, de l'enfant ou des deux ?
Données k = 1,00*10^3N.m^-1; = 250N.s.m^-1 ; z0 = 5 cm
Re,
En mécanique on commence toujours :
- par définir le système étudié ;
- le référentiel d'étude ;
- faire un bilan des efforts appliqués au système.
- accompagné d'un schéma :
extrait de 
la FAQ du forum :Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?
La première question relève du cours de terminale, tu as une idée pour démarrer ?
Bonjour Kandaina, Bonjour gbm
Je laisse gbm gérer ce sujet.
Juste une remarque pour signaler qu'une fiche existe sur la résolution de l'équation différentielle du deuxième ordre qui intervient à partir de la question II.1 (les trois premières pages en particulier) :
Voici ce que j'ai fait pour le moment mais je ne sais pas si j'ai oublié des choses et si je ne me suis pas trompée.
Bonjour Kandaina, Bonjour gbm
Je laisse gbm gérer ce sujet.
Juste une remarque pour signaler qu'une fiche existe sur la résolution de l'équation différentielle du deuxième ordre qui intervient à partir de la question II.1 (les trois premières pages en particulier) :
Bonjour vanoise,
Effectivement, cela va nous servir
@Kandaina :
- système : {siège + adulte ou enfant} de masse m et de centre d'inertie G ;
- référentiel : OK
- bilan des forces : OK mais n'oublie pas le nom de chacune d'elles (poids du système et force de rappel exercées par le ressort sur le système).
Ton schéma représente le ressort au repos.
Il faut désormais faire la même chose avec le système au repos : la longueur du ressort devient alors léq.
Tu as exprimé le principe fondamental de la statique : OK
Il faut désormais projeter la relation sur l'axe (Ox).
Que trouves-tu ?
Projection sur l'axe (Ox) :
-k(leq - l0) + mg = 0
d'où leq = l0 + (mg / k)
Et voici mon nouveau schéma avec leq :
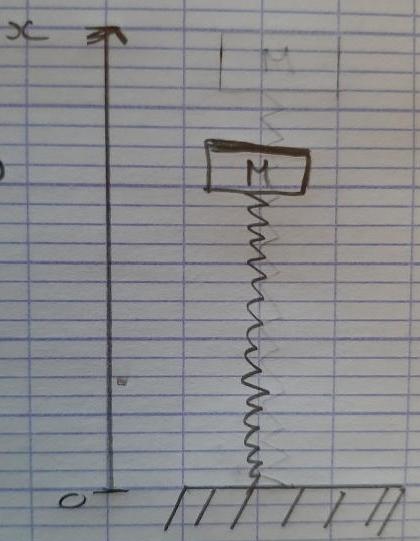
Je ne vois pas léq sur ton schéma, ni les forces en présence 
.
Attention à ta projection qui n'est pas correcte : ton axe est dirigé vers le haut donc
-k(leq - l0) - mg = 0
Ce qui fait :
leq = l0 - (mg / k) ce qui est physiquement plus acceptable, étant donné que ton ressort est comprimé --> sa longueur à l'équilibre sera plus petite qu'au repos !
Cette relation va te servir pour simplifier l'équation différentielle en étude dynamique ...
Oui, excuse moi, je me suis trompée de photo. Voici la bonne.
Du coup, les deux forces vont dans le même sens, n''est-ce pas ?
Merci beaucoup pour ton aide en tout cas !
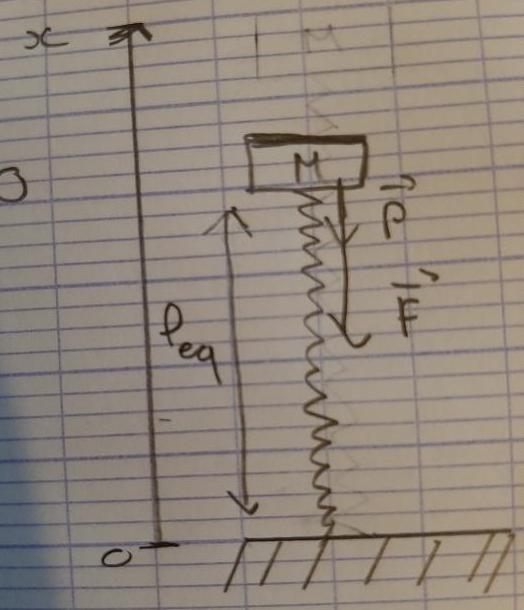
Tout est correct sauf ... le sens de la force de rappel !
La physique aime bien les situations les plus stables possible, en l'occurrence ici, le ressort aimerait retrouver sa longueur à vide.
Or étant donné qu'une masse m est posée dessus, la force de rappel va chercher à s'opposer au poids du système
C'est ce que je pensais. Le sens de la force de rappel me semblait étrange mais on a l'habitude de la mettre dans ce sens là d'où mon problème !
Le ressort est donc comprimé.
Raisonne sur la base des phénomènes physique : si quelqu'un s'asseyait sur toi, tu ferais tout pour le repousser non ? C'est pareil pour le ressort puisqu'il est effectivement comprimé !
Je te laisse réfléchir à l'étude dynamique :
- n'oublie pas le fichier fourni par vanoise ;
- mais aussi que la relation trouvée pour léq va permettre de simplifier l'équation différentielle.
J'ai regardé la fiche en question mais, soit ce n'était pas la bonne, soit je n'ai pas compris comment l'utiliser dans ma situation.
J'ai essayé mais j'ai du mal à débuter mon équation. Peux-tu m'aiguiller un peu s'il te plait ?
Bonjour,
Ta nouvelle position de référence est celle d'équilibre. Le tracteur entre dans un mouvement rectiligne uniforme avec d'autres conditions imposées par l'énoncé.
Il faut donc faire un nouveau bilan des forces en présence et appliquer le principe fondamental de la dynamique et aboutir à sa forme canonique rappelée dans l'énoncé.
C'est à partir de là que la fiche de vanoise va s'avérer utile, pour résoudre cette équation
Pour le nouveau bilan des forces, j'ai noté :
Poids du système : P = mgUx
Force de rappel : F = -k(l-l0)Ux
Frottements fluides : f=-v
Ensuite, d'après le PFD, on obtient : P + F + f = ma
Projection sur l'axe Ox :
mz"=-k(leq-l0)-mg ?
Annuler
connectez vous