Inscription / Connexion Nouveau Sujet
Aimant dans bobine
Bonjour,
je bloque sur la compréhension d'un énoncé : un aimant est tiré à vitesse constante sur l'axe d'une bobine de rayon a comportant N spires. On relie les bornes de la bobine à un oscilloscope.
On donne l'expression du champ magnétique : .
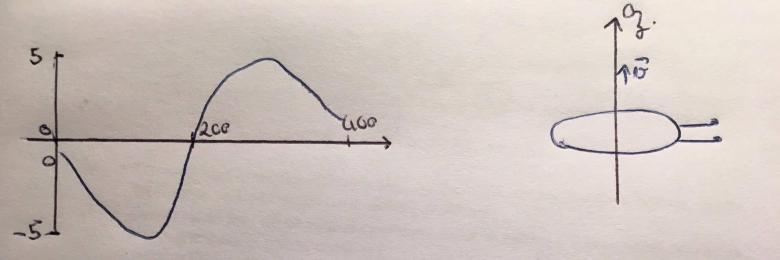
J'ai toute une série de questions où je dois trouver où se trouve l'aimant à t=200 ms, je dois donné l'expression de la tension en fonction des paramètres du problème et donner des valeurs approchées de
et
.
Mais déjà je ne comprends pas, quel est la relation entre la tension et le champ ?
Si quelqu'un pouvait me donner quelques pistes, ce serait super !
Merci d'avance et bonne soirée !
Bonsoir
Si tu notes 
le flux magnétique à travers la bobine du vecteur champ d'induction magnétique B créé par l'aimant, la bobine se comporte comme un générateur de force électromotrice :
L'oscillo, dont on peut considérer l'impédance d'entrée comme quasi infinie visualise donc les variations en fonction du temps t de e (ou -e : tout dépend des branchements).
Déplacer l'aimant le long de l'axe va donc créer quand l'aimant s'approche, une augmentation en fonction du temps de || puis une diminution de || quand l'aimant s'éloigne. Il faudrait un schéma précisant les pôles de l'aimant, le sens d'enroulement du fil conducteur de la bobine et les bornes de branchement à l'oscillo pour être capable d'algébriser correctement...
Annuler
connectez vous