Inscription / Connexion Nouveau Sujet
agrandisseur/réducteur d'image
Bonjour,
Je ne parvient pas à résoudre cet exercice:
On étudie un système de projection et reproduction de documents.
L'original, situé dans le plan P, est considéré comme l'objet et un système optique en forme une image, sur une vitre plane dans le plan P'. La distance D séparant les deux plans parallèles P et P' est fixée: D=0.427m.
1)Pour obtenir une image de même taille que l'objet (valeur absolue du grandissement égal à 1), peut on utiliser une unique lentille? Convergente, divergente? Si oui, préciser position et distance focale.
(J'ai dit que l'on pouvait utiliser une lentille convergente, que l'objet devait être situé entre l'infini et le foyer objet F par contre je ne trouve pas pour la distance focale).
2) On utilise en réalité un ensemble de 2 lentilles: une lentille L1 convergente et une lentille L2 divergente.
L1 est située à d=0.20m de P et L2 est située à d=0.20m de P'. On donne la distance focale de L2: f'2=-0.10m.
a) Dans quel plan doit se trouver l'image A1B1 donnée de l'objet AB par L1?
b) Quelle valeur donner à la distance focale f'1?
c) Calculer le grandissement ɣ de l'association L1-L2 pour l'objet AB?
3)a)Proposer une association donnant le grandissement 1/ɣ (objet et image restent en P et P').
b) On remplace la lentille L1 par une association de deux lentilles accolées: L2 et L3. Déterminer f'3.
c) Montrer qu'une association formée de deux lentilles fixes L2 et d'une lentille mobile L3 permet d'obtenir les grandissements ɣ et 1/ɣ par simple déplacement de L3.
Merci pour votre aide.
Bonjour,
Pour la 1, c'est un peu léger... Une lentille convergente, certes...
Donc :
En fait, on a :
avec x > 0
Donc :
Donc :
En conclusion, la distance objet-lentille est égale à la distance image-lentille et égale à 2 fois la distance focale...
C'est mieux, non ?
Avec une lentille divergente, ce n'est pas possible parce que, pour un image réelle, il faut un objet virtuel (situé entre la lentille et son plan focal objet)
Merci beaucoup pour votre réponse.
Pour la 1) ma lentille est bien située au milieu de P et P'? Du coup je pensais que f'=0.2135 (f'=D/2)
Pour la 2)a) A1B1 doit il être situé en L2?
Non,la lentille est bien à 0,427 / 2 = 0,2135 m de P et de P'(0,214 m parce que 3 chiffres significatifs) mais la distance focale est égale à la moitié : f' = 0,2135 / 2 = 0,10675 m (0,107 m parce que 3 chifffres significatifs)
OK ?
On s'occupe de la 2 après...
Il faut que l'image de A1B1 soit située dans le plan P'.
Ce qui donne :
(2 chiffres significatifs)
L'image A1B1, image de AB par L1, est à 7 cm derrière la lentille L2 donc à 97 mm de L1. C'est un objet virtuel pour L2.
ah d'accord merci beaucoup, je vais essayer de trouver la suite et je posterai mes résultats demain
par contre je ne vois pas du tout pour la 3)
Après avoir bien tout regardé je ne comprend pas comment on en déduit que A1B1 est à 97mm de L1.
Pour la 2b) j'ai calculé f'1 et j'obtient -0.19m ce qui n'est pas cohérent car L1 est une lentille convergente.
Pour la 2c) je voulais faire ɣ=1/f'1 + 1/f'2 avec la valeur trouvé précédemment de f'1 j'obtient ɣ= -15.3 ce qui me semble faux.
Par contre je n'ai rien pour la 3)
J'ai eu un problème avec mon pseudo donc j'en ai créé un autre...
Donc :
Un calcul plus exact en prenant au lieu de
donne
On a :
(2 chiffres significatifs)
Soit
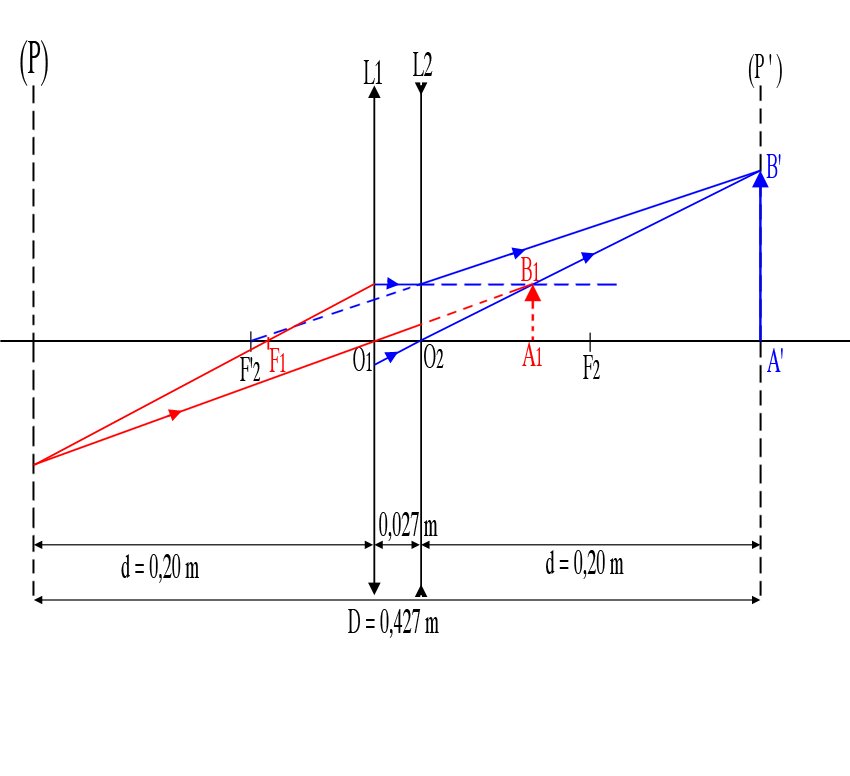
Merci beaucoup, c'est beaucoup plus clair
Pour le grandissement je trouve pareil c'est bien ɣ=O1A1/O1A * O2A'/O2A1 = 0.094/0.20 * 0.20/(0.20/3)=1.4 j'espère ne pas avoir tout mélangé.
Pour la 3)a) je pensais peut être à 2 lentilles divergentes...
Non, pour la 3a, pour obtenir 1/ , il faut permuter la distance objet-lentille et la distance image-lentille.
, il faut permuter la distance objet-lentille et la distance image-lentille.
Dans le dernier calcul, il y a une erreur de recopie mais je suppose que tu as corrigé...
Ce n'est pas mais
.
Désolé...
En mettant L1 à 0,2495 m de P et L2 à 0,1775 m de P', on obtient un grandissement de 1/ (avec
(avec  ayant la valeur trouvée précédemment, soit
ayant la valeur trouvée précédemment, soit 
 1,4).
1,4).
Ce n'est pas facile à expliquer mais je peux essayer quand même et j'ai mis un certain temps à trouver. Ce n'est pas la seule solution , bien entendu...
Oui j'avais vu, ce n'est pas grave
Donc si on permute la distance objet-lentille et image-lentille, l'image se retrouve en P et l'objet en P', cela ne revient il pas à positionner d'abord la lentille divergente puis la lentille convergente?
On a toujours la lentille convergente puis la lentille divergente.
Le raisonnement est basé sur le fait que, si on permute la distance objet-lentille et la distance image-lentille, on obtient 1/ . Cela est vrai pour n'importe quelle lentille.
. Cela est vrai pour n'importe quelle lentille.
Ici, le grandissement  =
=  1
1  2.
2.
Donc :
Donc il suffit d'inverser le grandissement pour chaque lentille pour obtenir .
Donc il faut permuter la distance objet-lentille et la distance image-lentille pour chaque lentille.
L'inconvénient est que la distance PP' est imposée et, dans ce cas, un objet en P n'a plus son image en P' quand on fait cette permutation.
Donc il y a un problème...
Jusque là, ça va ?
Pour résoudre ce problème, on va prendre des multiples des longueurs initiales.
Et:
Donc,en permutant les distances objet-lentille et image-lentille :
D'où le schéma joint...
On en déduit immédiatement que k1 > k2.
Et on a :
d'où :
On a aussi :
On doit avoir O1O2 > 0 évidemment...
On peut prendre k2 = 2, par exemple, ce qui donne :
On peut essayer d'avoir k1 = k2 = k :
Dans ce cas, O1O2 = 0 ( ==> les deux lentilles sont accolées).
Les valeurs de k1 et k2 permettent de calculer les positions des lentilles.
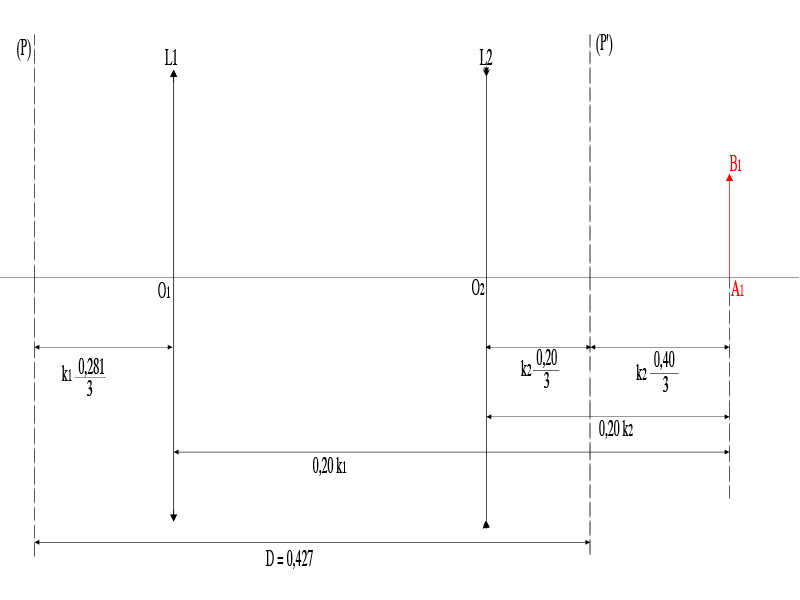
Il y a beaucoup de solutions possibles mais k1 et k2 ne peuvent quand même pas prendre n'importe quelle valeur.
Je rappelle que A1B1 est un objet virtuel donc il peut être en-dehors de PP'.
je suis désolée de répondre si tard.
Merci beaucoup pour votre explication.
Pour répondre à la 3b) ai-je le droit de me servir de la question précédente, en sachant que 1/ɣ=1/(1/f')=f' ?
Deux lentilles accolées sont équivalentes à une lentille dont la vergence est la somme des vergences des deux lentilles.
La somme des vergences des lentilles L2 et L3 doit être égale à la vergence de la lentille L1.
Donc 1/f'1=1/f'2 + 1/f'3
soit f'3=f'1f'2/f'2-f'1
f'3=0.039m si je ne me trompe pas.
Pour la 3c) je ne comprend pas vraiment car j'ai l'impression que c'est se qui a été fait précédemment...
j'ai retravaillé la question 3a) que vous m'avez expliqué et il y a quelque chose qui m'échappe comment a-t-on que k=k1=k2=1.281/0.881-0.40
Donc si on prend k=k1=k2=2.7 (on arrondi bien à 2 chiffres significatifs?) O1A=0.3m O1A1=0.54m O2A1=0.54m et O2A'=0.18m
donc ɣ1=1.8
ɣ2=0.33
d'où 1/ɣ=1.7 ?
la lentille L1 est donc à 0.3m de P et 0.18m de P' et L2 est à 0.247m de P et 0.18m de P'
J'ai repensé à quelque chose, pour la 3b) il faut peut être que je recalcule f'1 et f'2 avec les valeurs trouvées pour ɣ1 et ɣ2?
Pour la 3b, c'est correct.
Pour la 3a, tu as raison, il y a un problème... Une lentille divergente donne une image réelle dans un seul cas : un objet virtuel entre la lentille et le plan focal objet.
C'est à dire qu'il ne faut pas que je prenne k=k1=k2=2.7 pour obtenir ɣ=-1.4 ?
Par contre je ne comprend pas la 3c)
C'est à dire qu'il ne faut pas que je prenne k=k1=k2=2.7 pour obtenir ɣ=-1.4 ?
Non, on ne peut pas prendre k = 2,7 parce que l'objet virtuel A1B1 ne se trouve plus entre le plan focal objet et la lentille L2 (condition obligatoire pour avoir une image réelle avec une lentille divergente, image réelle droite et plus grande que l'objet donc on ne peut pas obtenir 1/G2 = 1/3 parce que G2 > 1 ).
Donc il faut abandonner la réponse que j'ai donnée. Ce n'est pas bon... On repart à zéro.
Cela fonctionne bien avec une lentille convergente. En échangeant les distances objet-lentille et image-lentille, on obtient 1/ G. Mais, avec une lentille divergente avec image réelle, c'est plus compliqué...
Donc la situation est la suivante :
- On a
- L'objet virtuel A1B1 doit se situer entre la lentille divergente L2 et son plan focal objet (G2 > 1) pour donner une image réelle au bon endroit (plan (P')).
- La lentille convergente L1 doit fournir l'objet virtuel A1B1 (qui est une image réelle pour L1) au bon endroit avec l'objet AB dans le plan (P).
- Le gain global doit être 1/
 :
: On a quelques degrés de liberté :
- sur O1A ou O1A1 parce que les deux sont liés
- sur O2A1 ou O2A' parce que les deux sont liés
Et il y a quelques contraintes (citées plus haut).
Je ne crois pas avoir oublié quelque chose.
Donc il faut réfléchir là-dessus...
-
Comment a-t-on ɣ=1.4?
comme 1/ɣ=1/ɣ1 + 1/ɣ2 et que ɣ1=O1A1/O1A et que ɣ2=O2A'/O2A1
alors 1/ɣ=O1A/O1A1 + O2A1/O2A' = 0.714
mais près je ne vois pas comment en déduire les positions des lentilles.
ah oui autant pour moi, je pense que je comprend mal la question, faut il juste que je détermine la valeur de 1/ɣ ou faut il que je dise à qu'elles distances sont situées L1 et L2.
Cela doit il entrer en compte pour la c)? car je ne sais pas se qu'il faut faire, en sachant que pour la b) j'ai f'3=0.039m
Pour la 3a
Il faut partir de ce que l'on connaît, autrement dit
On peut prendre pour L2 la même position donc :
On est obligé de faire ainsi parce qu'on ne peut pas avoir 1/3 vu que ...
Donc :
avec
On peut donc calculer
On a O1A, O2A' et on peut calculer O1O2 puisque :
(sans valeurs algébriques)
On a donc la position des lentilles
Merci pour votre reponse.
J'obtient AO1=1,02m et donc O1O2=-0,793m est ce normal avoir une valeur negative? Cela veut il dire que L2 est situe a 0,793m devant L1?
Bon, j'ai fini par trouver une vraie démonstration... (Ouf ! )
Le calcul est plutôt long donc je ne peux pas le recopier entièrement.
La relation de conjugaison pour L1 est :
D'où :
De même :
En suivant le même principe :
Et :
En remplaçant dans (1) :
On a :
Après quelques calculs, on trouve :
On trouve :
D'où deux racines :
Et :
==> impossible parce que G2 > 1
D'où :
De même :
Et :
(sans valeurs algébriques)
Tu peux faire tous les recoupements possibles. Cela fonctionne...


