Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... MasterForum Supérieur de master PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau master
Partager :

adaptation d'impedance

Posté par
zebrico 01-01-19 à 21:17

Bonjour à toutes et à tous,

Tout d'abord bonne année!
Ma question porte sur les impédances des lignes coaxiales et entre la version de mon prof, les versions que je trouve sur internet et ma version, ça ne concorde pas trop...

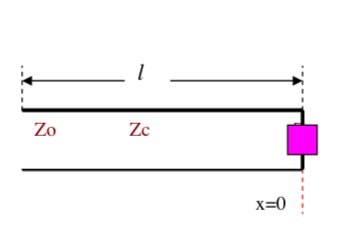
Voici la ligne étudiée ( figure en pièce jointe ) ( , page 20 )

Pour rappel voici l'expression du taux de réflexion :

\Gamma(x)=\Gamma_o\cdot e^{-i\cdot 2\cdot\beta\cdot x}\leftrightarrow\Gamma(l-s)=\Gamma_t\cdot e^{-i\cdot2\cdot\beta\cdot s}


et dans le cours de mon prof j'ai la relation suivante pour l'impédance réduite à l'abscisse s :

z_r(s)=\dfrac{z_t+i\cdot tan(\beta\cdot s)}{1+i\cdot z_t\cdot tan(\beta\cdot s)}

sachant qu'il dit qu'il faut utiliser la relation suivante :

\Gamma_t=\dfrac{z_t-1}{z_t+1}

Le problème est que je n'obtiens pas tellement ce résultat. J'obtient le résultat suivant :

z_r(s)=A(z_t)\cdot\dfrac{B(z_t)-i\cdot tan(\beta\cdot s)}{1+i\cdot A(z_t)\cdot tan(\beta\cdot s)}

avec :

A(z_t)=\dfrac{2\cdot\Gamma_t\cdot cos(\beta\cdot s)^2}{1-\Gamma_t\cdot cos(2\cdot \beta\cdot s)}

et :

B(z_t)=\dfrac{1+\Gamma_t\cdot cos(2\cdot \beta \cdot s)}{2\cdot\Gamma_t\cdot cos(2\cdot \beta\cdot s)^2}

Sachant que dans le lien que j'ai donné ils obtiennent encore une autre relation j'ai l'impression ( relation 26 page 2o ). Dans un cours de l'ENS  ( slide 11o ) ils donnent encore autre chose...

Du coup ma question n'est pas de revérifier mes calculs ( même si je ne suis pas contre, en 5 lignes c'est fait ) mais plutôt de me dire qui à raison ...

en vous remerciant par avance,

adaptation d\'impedance

Posté par
vanoisere : adaptation d'impedance 02-01-19 à 13:50

Bonjour
Difficile de t'aider car tu utilises des notations qui ne sont définies ni dans ton message ni dans le document dont tu fournis le lien.
J'ai d'abord cru comprendre que s désigne l'abscisse mesurée à partir de la charge : s=0 sur la charge et s = L à l'entrée de ligne mais le schéma que tu joins précise x=0 sur la charge ???
Je pense : Zo : impédance d'entrée, Zc :  impédance caractéristique (impédance itérative). Je suppose :
z_{r}(s)=\frac{v(s)}{i(s)}
mais que désigne zt ???
Le premier document cité en référence  contient aussi des erreurs : certaines relations dites "trigonométriques" font intervenir "j" et j'ai remarqué quelques erreurs dans les calculs en complexes...

Posté par
zebricore : adaptation d'impedance 02-01-19 à 15:09

Bonjour Vanoise,

Oui en effet j'avais en tête le schéma de mon cours où c'est bien la convention que vous aviez en tête au tout début.
Quant à Zo c'est l'impédance du câble coaxial seul.
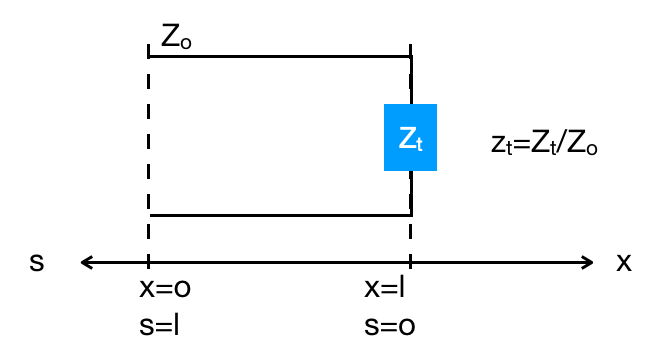
Ensuite z_t est l'impédance réduite telle que :

z_t=\dfrac{1+\Gamma_t}{1-\Gamma_t}

Avec :

\Gamma_t=\Gamma_o\cdot e^{-2\cdot i\cdot\beta\cdot l}

Puis

\Gamma_o=\dfrac{amplitude\ potentiel\ incident}{amplitude\ potentiel\ reflechi}

et

\beta=\nicefrac{2\cdot\pi}/{\lambda}

est ce que c'est mieux?
merci encore

adaptation d\'impedance

Posté par
vanoisere : adaptation d'impedance 02-01-19 à 18:18

Citation :
Quant à Zo c'est l'impédance du câble coaxial seul.

Je ne comprends pas la signification de cette phrase...
L'impédance caractéristique de la ligne (aussi appelée impédance itérative) dépend uniquement des caractéristiques de la ligne : son inductance linéique et sa capacité linéique). Elle est parfois notée Zo mais la plupart des cours la note Zc. Est-ce bien le cas ici ?
Dans ce cas, Zo pourrait désigner l'impédance d'entrée de la ligne, celle mesurée en x=0 ou s=L , lorsque la charge est branchée.
La plupart des auteurs définissent l'impédance réduite en divisant l'impédance en x ou l'impédance en s par Zc et non par Zo comme indiqué sur ton schéma...

Posté par
zebricore : adaptation d'impedance 02-01-19 à 19:14

La ligne coaxiale est composée d'un diélectrique de permittivité  \varepsilon
et de perméabilité \mu et donc d'impédance Z_o=\sqrt{\mu/\varepsilon}

tout simplement

après j'ai suivi mon cours... mon prof étant opticien et non télégraphiste, je ne fais que suivre ses notations. Après que Z_c=Z_o... ok si vous voulez ...

Posté par
vanoisere : adaptation d'impedance 02-01-19 à 19:19

D'accord mais ton premier schéma faisait intervenir à la fois un Zo et un Zc ; dans ces conditions, il est légitime de penser qu'il s'agit de deux grandeurs différentes !

Posté par
vanoisere : adaptation d'impedance 02-01-19 à 19:56

J'arrive effectivement au résultat de ton professeur. Je te donne les grandes lignes. Pose des questions complémentaires si tu le juges utile.
Je choisis l'origine sur la charge ; ainsi l'onde incidente se propage dans le sens négatif de s et l'onde réfléchie dans le sens positif de s : le potentiel (notations complexes) à l'abscisse s est ainsi :

v=v_{i}.\exp\left(j.\beta.s\right)+v_{r}.\exp\left(-j.\beta.s\right)

i=\dfrac{1}{Z_{c}}.\left[v_{i}.\exp\left(j.\beta.s\right)-v_{r}.\exp\left(-j.\beta.s\right)\right]

D'où l'impédance réduite à l'abscisse s :

z_{r}=\dfrac{v}{Z_{c}.i}=\dfrac{v_{i}.\exp\left(j.\beta.s\right)+v_{r}.\exp\left(-j.\beta.s\right)}{v_{i}.\exp\left(j.\beta.s\right)-v_{r}.\exp\left(-j.\beta.s\right)}=\dfrac{\exp\left(j.\beta.s\right)+\varGamma_{t}.\exp\left(j.\beta.s\right)}{\exp\left(j.\beta.s\right)-\varGamma_{t}.\exp\left(j.\beta.s\right)}

Attention : l'origine des abscisses étant choisie sur la charge, le rapport \left(\dfrac{v_{r}}{v_{i}}\right) vaut \Gamma_{t} et non \varGamma_{o}.

z_{r}=\dfrac{\left(z_{t}+1\right).\exp\left(j.\beta.s\right)+\left(z_{t}-1\right).\exp\left(-j.\beta.s\right)}{\left(z_{t}+1\right).\exp\left(j.\beta.s\right)-\left(z_{t}-1\right).\exp\left(-j.\beta.s\right)}

En remplaçant les exponentielles par leurs expressions en fonction des sinus et cosinus puis en divisant tous les termes par 2.\cos\left(\beta.s\right) on obtient l'expression de ton professeur.

Posté par
vanoisere : adaptation d'impedance 02-01-19 à 23:09

Etourderie dans l'utilisation de l'éditeur d'équation à l'avant dernière formule. Cette étourderie ne se répercute pas ensuite. Je rectifie tout de même :

z_{r}=\dfrac{v}{Z_{c}.i}=\dfrac{v_{i}.\exp\left(j.\beta.s\right)+v_{r}.\exp\left(-j.\beta.s\right)}{v_{i}.\exp\left(j.\beta.s\right)-v_{r}.\exp\left(-j.\beta.s\right)}=\dfrac{\exp\left(j.\beta.s\right)+\varGamma_{t}.\exp\left(-j.\beta.s\right)}{\exp\left(j.\beta.s\right)-\varGamma_{t}.\exp\left(-j.\beta.s\right)}

Posté par
zebricore : adaptation d'impedance 03-01-19 à 14:34

Bonjour Vanoise,

En partant de la définition ça marche bien on est d'accord mais je me demande pourquoi ça ne marche pas en partant de

z_r(l-s)=\dfrac{1}{Z_o=Z_C}\cdot\dfrac{1+\Gamma(l-s)}{1-\Gamma(l-s)}

et puisque tous les autres partent de la définition c'est ce que je vais faire mais me chiffonne quand même..

merci encore!

Posté par
vanoisere : adaptation d'impedance 03-01-19 à 15:29

J'ignore tout des exigences de ton professeur. J'ai donc préféré repartir « de la base ». Tu peux éventuellement partir de la relation de l'impédance réduite :

z_{r}=\dfrac{1+\varGamma}{1-\varGamma}

Attention : l'impédance réduite est une grandeur de dimension un (sans dimension comme on dit encore parfois) ; l'impédance caractéristique n'intervient pas ici.
D'autre part : on choisit l'origine des abscisses au niveau de la charge. On obtient donc à l'abscisse s :

\varGamma=\varGamma_{t}\cdot\exp\left(-2\beta.s\right)

ce qui conduit simplement à :

z_{r}=\dfrac{1+\varGamma_{t}\cdot\exp\left(-2\beta.s\right)}{1+\varGamma_{t}\cdot\exp\left(-2\beta.s\right)}

En multipliant tous les termes par \exp\left(\beta.s\right), on obtient l'expression fournie dans mon message précédent.

Posté par
zebricore : adaptation d'impedance 03-01-19 à 15:58

Vous avez raison de partir de la définition, réflexe que je devrais tout le temps avoir normalement...

oui pour l'impédance réduite, qui tire bien son nom... étourderie de ma part..

et multiplier en haut et en bas par l'exponentielle est une idée assez basique, j'ai un peu honte de ne pas l'avoir vu..

Merci encore et toujours!


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !