Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

Action d'un filtre passe haut

Posté par
pfff 08-01-21 à 23:06

Bonsoir j'ai besoin d'aide pour ce problème merci.

ENONCE

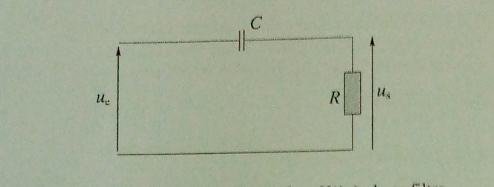
On étudie l'action d'un filtre représenté ci dessous sur différents signaux en regime forcé.

1. Déterminer la fonction de transfert H(j) de ce filtre.
Tracer le diagramme de Bode.

2. ue est une tension constante. Déterminer us(t) en régime établi.

3. ue(t) = Uo [ 1 + cos(2ft) ]. Uo est une constante homogène à une tension et f = 20 kHz.

4. ue(t) = Uo cos^3(2ft) avec 2ft = 250 s^-1

Sachant que :

cos^3x = (1/4) [ cos(3x) + 3 cos(x) ]

écrire l'expression de us(t) en regime établi.

Quelle est la sortie si du bruit se superpose au signal d'entrée ?


5. ue(t) est une fonction créneau de fréquence f telle que 2f = 250s^-1
On ne cherchera que l'allure de la tension de sortie us.

REPONSE

J'ai pu faire la premiere question je ne comprends pas les suivantes

Posté par
pfffre : Action d'un filtre passe haut 08-01-21 à 23:08

Action d\'un filtre passe haut

Posté par
gts2re : Action d'un filtre passe haut 09-01-21 à 06:27

Bonjour,

Il manque une donnée : la fréquence de coupure du filtre

2- Quelle est la définition d'un passe-haut ? Ou encore plus simple, à quoi est équivalent le schéma en continu.

Pour les suivants, la première chose à faire est de comparer la fréquence à la fréquence de coupure du filtre, et en absence de celle-ci ...

Posté par
pfffre : Action d'un filtre passe haut 09-01-21 à 13:20

Citation :
Il manque une donnée : la fréquence de coupure du filtre

J'ai pas bien compris ce message.

2. en continu le condensateur se comporte comme un interrupteur ouvert

on aura us = 0

3. je determine comment la frequence de coupure ?

Posté par
gts2re : Action d'un filtre passe haut 09-01-21 à 13:34

2- OK

3-
Tout dépend où vous en êtes dans votre cours, si vous avez suffisamment avancé, vous connaissez la forme "canonique" d'un filtre passe-haut du premier ordre et il y a juste à identifier.

Sinon vous avez tracé le diagramme de Bode, et pour cela il faut bien connaitre la fréquence de coupure (où se trouve-t-elle dans un diagramme de Bode ?)

Citation :
J'ai pas bien compris ce message : "Il manque une donnée : la fréquence de coupure du filtre"

L'effet d'un filtre sur un signal dépend de la fréquence de coupure du filtre, si on ne connait pas la fréquence de coupure, on ne peut tout simplement rien faire.

Posté par
pfffre : Action d'un filtre passe haut 09-01-21 à 13:43

ce filtre est de la forme \bar{H(j\omega )} = \frac{jx}{1+jx} avec w_0 = \frac{1}{RC} et x = \frac{\omega }{\omega _0}

pour determiner us(t) dans la 3e question vous dites que je dois comparer sa fréquence à la fréquence du coupure du filtre. Dans le cas où la fréquence de coupure est plus grande comment je determine us(t) ?

Posté par
gts2re : Action d'un filtre passe haut 09-01-21 à 13:48

Donc vous connaissez la fréquence de coupure littérale, mais pour aller plus loin, il faut une valeur numérique : pour Q3, la première chose à faire est de placer 20 kHz par rapport à la fréquence de coupure.

Posté par
pfffre : Action d'un filtre passe haut 09-01-21 à 14:15

J'ai oublié de donner les données du filtres : R = 2k et C = 1 F

D'accord la frequence de coupure du filtre est c = 0 = 500 rad/s

donc fc = 79.58 Hz or f = 20000 Hz

on a évidemment fc < f

Posté par
gts2re : Action d'un filtre passe haut 09-01-21 à 14:19

Et même f \gg f_c, donc la sortie us(t) = ?

Posté par
pfffre : Action d'un filtre passe haut 09-01-21 à 14:32

je comprends pas bien comment on pourra determiner us(t) avec cette relation

Posté par
gts2re : Action d'un filtre passe haut 09-01-21 à 14:39

Quelle est la définition d'un passe-haut ?

Posté par
pfffre : Action d'un filtre passe haut 09-01-21 à 14:44

filtre transmet les signaux de hautes fréquences et atténue ceux de
basses fréquences

Posté par
gts2re : Action d'un filtre passe haut 09-01-21 à 14:50

Et donc pour le signal 3 ?

Posté par
pfffre : Action d'un filtre passe haut 09-01-21 à 15:02

us = 0

Posté par
gts2re : Action d'un filtre passe haut 09-01-21 à 15:27

On vient de dire que f_{signal} \gg f_{coupure} que le filtre transmet les signaux de hautes fréquences et vous trouvez us(t) = 0 ?

Ceci étant, il faut faire attention à ce que ue(t) =Uo  + Uo cos(2ft), donc avec deux composantes

Posté par
pfffre : Action d'un filtre passe haut 09-01-21 à 15:38

je vois il va laisser passer les hautes frequences donc us = ue

Posté par
gts2re : Action d'un filtre passe haut 09-01-21 à 15:42

J'ai bien dit qu'il fallait faire attention aux deux composantes :
- qu'arrive-t-il à Uo ?
- qu'arrive-t-il à  Uo cos(2ft) ?

Posté par
pfffre : Action d'un filtre passe haut 09-01-21 à 15:55

Uo s'annule et Uo cos(2ft) reste

Posté par
gts2re : Action d'un filtre passe haut 09-01-21 à 16:03

OK, c'est bien cela

Pour la suite, cela se complique, la fréquence du signal est voisine de la fréquence de coupure. Il va cette fois falloir calculer.

Posté par
pfffre : Action d'un filtre passe haut 09-01-21 à 16:13

je réécris ue(t)

ue(t) = \frac{1}{4}U_0cos(6\pi ft ) + \frac{3}{4}U_0cos(2\pi ft)

fsignal = 39,79 Hz

donc fcoupure > fsignal

Posté par
gts2re : Action d'un filtre passe haut 09-01-21 à 16:19

Oui mais pour les calculs, il vaut mieux raisonner en pulsation.

Posté par
pfffre : Action d'un filtre passe haut 09-01-21 à 16:36

c = 500 rad/s et signal = 250 rad/s

Posté par
gts2re : Action d'un filtre passe haut 09-01-21 à 16:38

Donc pour le calcul du terme en f : \frac{\omega}{\omega_c}=\frac 12

Posté par
pfffre : Action d'un filtre passe haut 09-01-21 à 16:52

que dois faire de cette fréquence ?

Posté par
gts2re : Action d'un filtre passe haut 09-01-21 à 16:56

Il s'agit maintenant simplement d'appliquer la définition  de H : H=\frac{\underline{U_s}}{\underline{U_s}}

Posté par
pfffre : Action d'un filtre passe haut 09-01-21 à 17:11

H=\frac{\underline{U_s}}{\underline{U_s}} =  \frac{jx}{1+jx}[/tex]

je remplace x par 1/2

Posté par
pfffre : Action d'un filtre passe haut 09-01-21 à 17:13

pfff @ 09-01-2021 à 17:11

H=\frac{\underline{U_s}}{\underline{U_s}} =  [/tex]\frac{jx}{1+jx}[/tex]

je remplace x par 1/2  ?

Posté par
gts2re : Action d'un filtre passe haut 09-01-21 à 17:17

Par définition même.

Posté par
pfffre : Action d'un filtre passe haut 09-01-21 à 17:22

lorsque j'aurai remplacé je cherche il y aura des complexes dedans comment je pourrai determiner us(t)

Posté par
pfffre : Action d'un filtre passe haut 09-01-21 à 17:31

Citation :
lorsque j'aurai remplacé je cherche il y aura des complexes dans l'expression de H comment je pourrai determiner us(t)

Posté par
gts2re : Action d'un filtre passe haut 09-01-21 à 17:32

Quel est le complexe associé à A \cos(\omega t +\phi) ?

Posté par
pfffre : Action d'un filtre passe haut 09-01-21 à 17:53

il s'agit de \bar{A}e^{j\omega t } avec \bar{A} = Ae^{j\varphi }


Posté par
gts2re : Action d'un filtre passe haut 09-01-21 à 18:04

Bien, vous savez donc comment passer de u(t) à l'amplitude complexe associée et réciproquement.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !