Inscription / Connexion Nouveau Sujet
4 Ressorts sur un cercle
Salut,
Je suis bloqué sur l'exercice suivant:
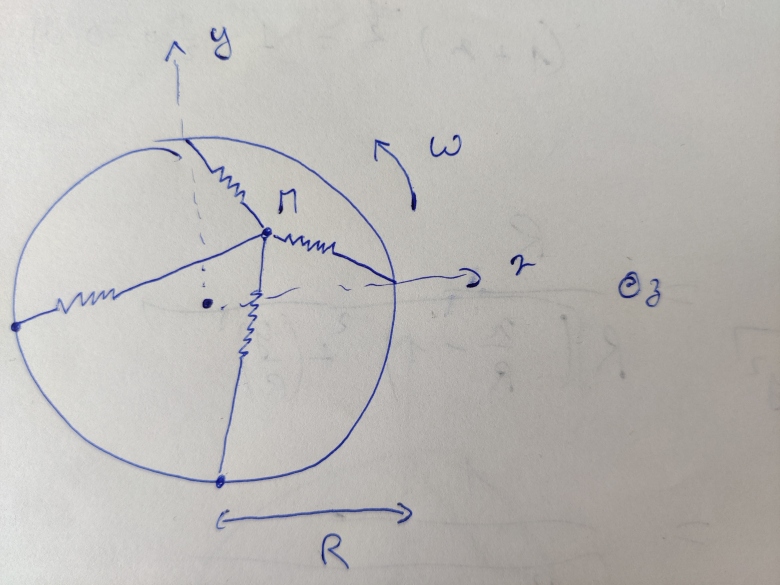
On s'intéresse au mouvement d'un point M de masse m relié à 4 ressorts de constante de raideur k et de longueur à vide R. Les ressorts sont accrochés aux 4 extrémités d'un cercle de rayon R en rotation à la vitesse constante (cf figure ci-dessous).
1) Déterminer la résultante des forces de rappel élastique.
J'ai trouvé
2) Déterminer l'équation du mouvement et la résoudre.
Pour cela je me suis placé dans le référentiel du cercle et j'ai appliqué le PFD: avec
la vitesse relative au référentiel du cercle et
sa dérivée.
J'obtiens le système et
que je ne sais pas résoudre...
Ai-je fais une erreur?
Bonsoir
une des méthodes possibles de découplage consiste à introduire la variable u=x+i.y
Tu multiplies ta seconde équation différentielle par "i" et tu additionne membre à membre avec la première.Tu vas obtenir une équation différentielle vérifiée par la seule inconnue "u".
Je vais vérifier ton travail d'ici ce soir.
J'imagine qu'il faut considérer les variations de longueurs des ressorts très petites devant R, sinon l'expression de la force élastique est nettement plus compliquée me semble-t-il...
D'accord avec tes calculs dans ces conditions.La méthode d'utilisation de la variable complexe u est ainsi une bonne méthode pour passer de tes deux équations différentielles couplées à une équation différentielle du deuxième ordre très classique.
rem1 : puisque, par hypothèse, M reste proche du centre O du cercle, la force de rappel élastique est nettement plus force que la force centrifuge : 2k>m 2 . On peut poser :
2 . On peut poser :
Les équations différentielles couplées s'écrivent ainsi plus simplement :
rem2 : ce problème présente une analogie forte avec l'étude du pendule de Foucault...
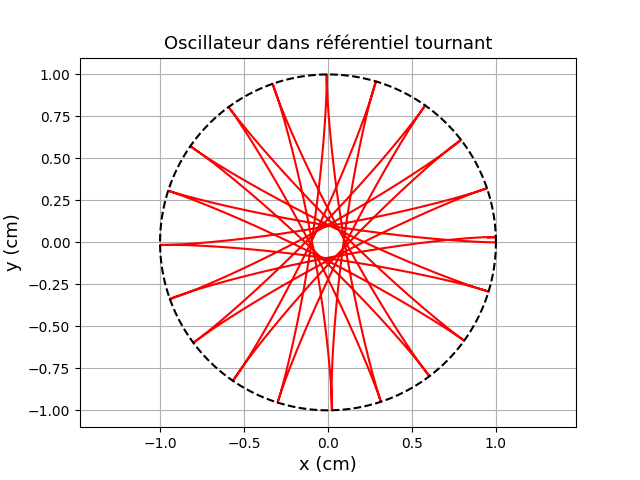
Voici une simulation de la trajectoire avec pour conditions initiales :
xo=1cm
yo=0
vitesse initiale nulle
 =10rad/s
=10rad/s
 =1rad/s
=1rad/s
N'hésite pas à poser des questions complémentaires si tu le juges utile. Si j'ai le temps, je posterai une simulation du mouvement si cela est accepté par le forum.