Inscription / Connexion Nouveau Sujet
2nde loi Newton
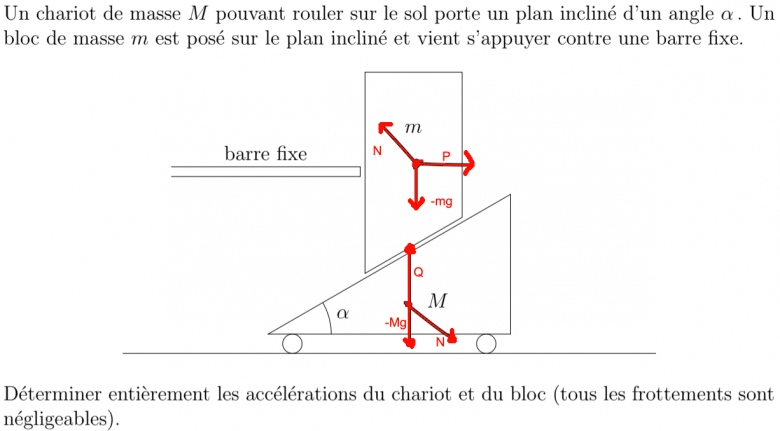
Bonjour je dois trouver l'accélération du chariot et de l'objet posé dessus dans ce schéma.
J'ai fait le diagramme des forces pour ensuite appliquer la 2nde loi de Newton mais je crois que je loupe quelque chose.
Je prends le repère orthogonal habituel (est-nord) et je me retrouve avec les systèmes suivants :
Pour l'objet de masse m d'accélération a :
Pour le chariot de masse M d'accélération A :
Et je n'aboutis à rien avec cela.
Quelqu'un pourrait-il me filer un coup de main ?
Bonjour
Il faut penser au principe des actions réciproques. Si les frottements sont négligées , les réactions sont normales aux surfaces de contact.
autres remarques : a cause de la barre fixe, l'accélération du bloc est nécessairement verticale et l'accélération du chariot est nécessairement horizontale. Il existe une relation entre ces deux accélérations et sin(
).
Méthode alternative à la tienne sans doute un peu plus simple : tenir compte de mon message de 17h34 et considérer qu'en absence de frottement, l'énergie mécanique de l'ensemble {bloc - chariot} se conserve.
autres remarques : a cause de la barre fixe, l'accélération du bloc est nécessairement verticale et l'accélération du chariot est nécessairement horizontale. Il existe une relation entre ces deux accélérations et sin(
).Effectivement c'est la raison pour laquelle je mets ax = 0 (1er systeme, 1ere ligne) et Ay=0(2e systeme, 2e ligne) mais il y a 5 inconnues pour 4 lignes...
Il te manque la relation entre A et a...
Lorsque le centre d'inertie du bloc subit un déplacement vertical z vers le bas, quel est le déplacement horizontal x du centre d'inertie du chariot vers la droite ? Une fois que tu auras trouvé cette relation qui fait intervenir en fait tan(), ton problème sera pratiquement terminé... Pense aussi, si tu as le temps, à la méthode utilisant la conservation de l'énergie mécanique ; elle est plus simple.
Il te manque la relation entre A et a...
Lorsque le centre d'inertie du bloc subit un déplacement vertical z vers le bas, quel est le déplacement horizontal x du centre d'inertie du chariot vers la droite ?
Je ne sais franchement pas. Je n'ai pas de passage du cours se référence aux changements de déplacement de centres d'inertie.
Pense aussi, si tu as le temps, à la méthode utilisant la conservation de l'énergie mécanique ; elle est plus simple.
Un déplacement horizontal d'une distance x du chariot vers la droite fait descendre le bloc verticalement d'une hauteur : z=x.tan(). En dérivant cette relation par rapport à t, tu obtient une relation entre la vitesse v du bloc et la vitesse V du chariot. Dériver par rapport au temps cette relation fournit la relation entre l'accélération "a" et l'accélération "A".
Sinon, dériver par rapport au temps l'expression traduisant la conservation de l'énergie mécanique conduit directement au résultat sans faire intervenir les forces de contact entre bloc et chariot.
Un déplacement horizontal d'une distance x du chariot vers la droite fait descendre le bloc verticalement d'une hauteur : z=x.tan(
). En dérivant cette relation par rapport à t, tu obtient une relation entre la vitesse v du bloc et la vitesse V du chariot. Dériver par rapport au temps cette relation fournit la relation entre l'accélération "a" et l'accélération "A".Effectivement vous aviez raison j'y suis arrivé, il s'agissait de z = - x tan(a) petite erreur de signe mais rien de méchant. Merci beaucoup.
il s'agissait de z = - x tan(a)
Le signe dépend de l'orientation des axes :
- signe "+" comme je l'avais écrit si l'axe des z est orienté verticalement vers le bas et l'axe des x horizontalement vers la droite ;
- signe "-" correct si l'axe des z est orienté verticalement vers le haut et l'axe des x horizontalement vers la droite.
Annuler
connectez vous