Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

2 équations différentielles du mouvement

Posté par
khalido 13-12-19 à 08:30

polaires
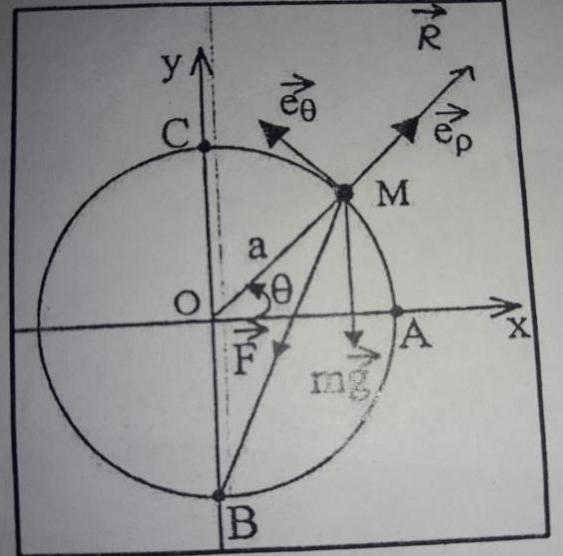
Un anneau schématisé par une particule M de masse m , peut glisser sans frottement sur un cercle de centre O et de rayon a , dans un plan vertical fixe (x,y) . À l'instant initial , il se trouve au point C avec une vitesse initiale quasi-nulle (voir figure).
En plus de son poids mg , il est soumis de la part du point B à une force d'attraction proportionnelle à la distance ||BM||vec , soit F vec = -kBM vec , k est une constante positive .
À chaque instant on repère la position de M dans le plan (xOy), supposé galiléen , par ses coordonnées polaires (a , (t) )
1- Donner dans la base ( e , e )
les composantes des vecteurs vitesse et accélération du point M à l'instant t
2- En projetant le PFD dans la même base déterminer 2 équations différentielles du mouvement .
3 - intégrer par rapport à (t) l'équation différentielle suivant e en déduire alors la réaction R exercée par le cercle sur le point M en fonction de mg , a , k et l'angle (t) .

j'ai fait la première question
mais pour la deuxième je sais pas ce que je dois faire ?
qu'est ce qu'on veut dire par les 2 équations différentielles ?

2 équations différentielles du mouvement

Posté par
diracre : 2 équations différentielles du mouvement 13-12-19 à 08:41

Bonjour,

Peut être pourrais tu partager les résultats que tu obtiens à la 1ere question?

Une équation différentielle est une équation qui lie une fonction et ses dérivées successives. Ici en projetant sur les axes comme demandé, tu obtiens 2 équation liant

r,  dr/dt, d2r/dt2, , d/dt, d2/dt2

Posté par
diracre : 2 équations différentielles du mouvement 13-12-19 à 08:43

Bien sur ce qu'il faut projeter, c'est la relation vectorielle:

\Sigma \vec{Forces} = m\vec{a}

Posté par
diracre : 2 équations différentielles du mouvement 13-12-19 à 08:55

Et bien sûr mon vecteur a n'est pas le a de l'énoncé (que je viens seult de lire ) qui désigne lui le rayon du cercle ...
La trajectoire étant d'ailleurs circulaire les dérivées successives de la 1ere coordonnée polaire (que j'ai appelée r) se déduisent rapidement )

Posté par
khalidore : 2 équations différentielles du mouvement 13-12-19 à 09:03

dirac @ 13-12-2019 à 08:41

Bonjour,

Peut être pourrais tu partager les résultats que tu obtiens à la 1ere question?

Une équation différentielle est une équation qui lie une fonction et ses dérivées successives. Ici en projetant sur les axes comme demandé, tu obtiens 2 équation liant

r,  dr/dt, d2r/dt2, , d/dt, d2/dt2


j'ai trouvé pour la vitesse : V = Rwe
pour l'accélération j'ai trouvé -Rw^2 e

Posté par
khalidore : 2 équations différentielles du mouvement 13-12-19 à 09:07

dirac @ 13-12-2019 à 08:43

Bien sur ce qu'il faut projeter, c'est la relation vectorielle:

\Sigma \vec{Forces} = m\vec{a}


Cette projection est correcte ?
P = -Pe
F = -Rcose - Rsine

2 équations différentielles du mouvement

Posté par
diracre : 2 équations différentielles du mouvement 13-12-19 à 09:27

ok pour la vitesse

(\omega = \dot{\theta})

Par contre pour l'accélération tu fais l'hypothèse que (\ddot{\theta}=0). Hum hum, pourquoi cela?

Tes projections de \vec{P} et \vec{F} sur les axes posent également problème.

\vec{P} = -mg\vec{j} avec la relation de chgt de repère \vec{j}=sin\theta\vec{e}_{\rho} + cos\theta\vec{e}_{\theta}

Tu reprends?

Posté par
khalidore : 2 équations différentielles du mouvement 13-12-19 à 09:36

dirac @ 13-12-2019 à 09:27

ok pour la vitesse

(\omega = \dot{\theta})

Par contre pour l'accélération tu fais l'hypothèse que (\ddot{\theta}=0). Hum hum, pourquoi cela?

Tes projections de \vec{P} et \vec{F} sur les axes posent également problème.

\vec{P} = -mg\vec{j} avec la relation de chgt de repère \vec{j}=sin\theta\vec{e}_{\rho} + cos\theta\vec{e}_{\theta}

Tu reprends?


Non j'ai pas fais ça
en dérivant la vitesse on obtient l'accélération et puis j'ai trouvé le résultat que j'ai déjà écrit
Pour les projections
si je projette premièrement sur l'axe xOy ça sera mieux et plus facile ?

Posté par
diracre : 2 équations différentielles du mouvement 13-12-19 à 09:53

Re hum hum

En coordonnées polaires:

\vec{v} = \dot{\rho}\vec{e}_\rho + \rho\dot{\theta}\vec{e}_\theta

\vec{a} = (\ddot{\rho}-\rho\dot{\theta}^2)\vec{e}_\rho + (2\dot{\rho}\dot{\theta}+\rho\ddot{\theta})\vec{e}_\theta

avec dans le cas de cet exercice = a = constante

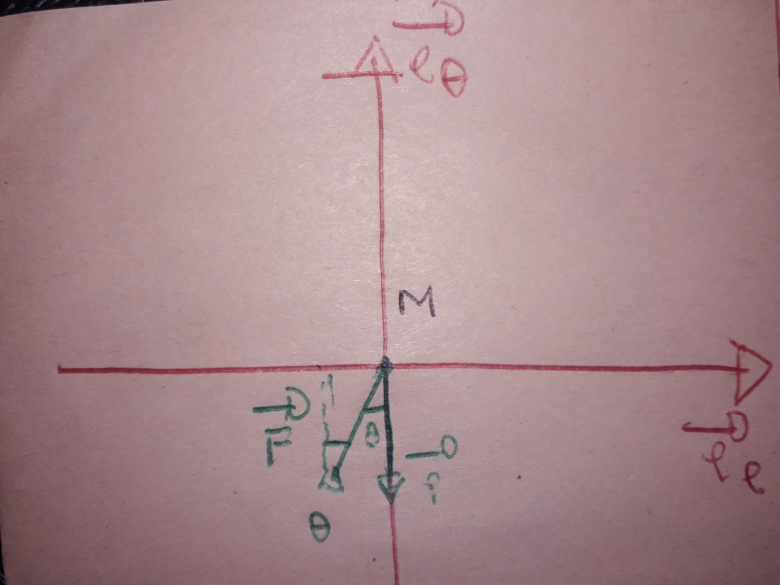
Concernant la projection sur les axes. Non il n'est pas nécessaire de revenir aux projections sur xOy,  j'illustrais simplement ton erreur par un "test" simple sur le poids qui est colinéaire à Oy

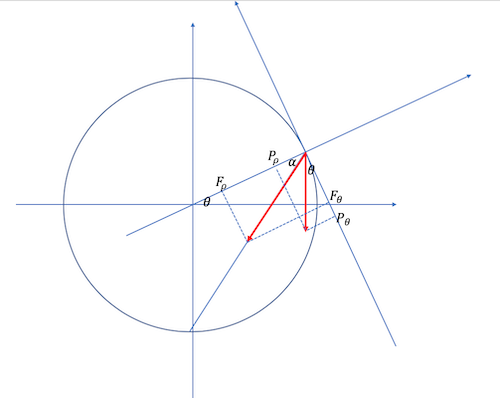
Pendant que tu cherches à rectifier , je fais un crobard puis je partage avec toi

Posté par
khalidore : 2 équations différentielles du mouvement 13-12-19 à 10:20

dirac @ 13-12-2019 à 09:53

Re hum hum

En coordonnées polaires:

\vec{v} = \dot{\rho}\vec{e}_\rho + \rho\dot{\theta}\vec{e}_\theta

\vec{a} = (\ddot{\rho}-\rho\dot{\theta}^2)\vec{e}_\rho + (2\dot{\rho}\dot{\theta}+\rho\ddot{\theta})\vec{e}_\theta

avec dans le cas de cet exercice = a = constante

Concernant la projection sur les axes. Non il n'est pas nécessaire de revenir aux projections sur xOy,  j'illustrais simplement ton erreur par un "test" simple sur le poids qui est colinéaire à Oy

Pendant que tu cherches à rectifier , je fais un crobard puis je partage avec toi


Franchement je suis perturbé maintenant
car dans le cours que j'ai appris tous ce que j'ai trouvé est correcte si le vecteur position OM = Re on va trouver ces résultats

Posté par
diracre : 2 équations différentielles du mouvement 13-12-19 à 10:21

Alors

\vec{P} = -sin\theta\vec{e}_\rho - cos\theta\vec{e}_\theta

\vec{F} = -cos\alpha\vec{e}_\rho - sin\alpha\vec{e}_\theta

Je te laisse calculer en fonction de   ?

2 équations différentielles du mouvement

Posté par
diracre : 2 équations différentielles du mouvement 13-12-19 à 10:29

Citation :
Franchement je suis perturbé maintenant
car dans le cours que j'ai appris tous ce que j'ai trouvé est correcte si le vecteur position OM = Re on va trouver ces résultats


Ben on n'a pas suivi les mêmes alors ....

Tu ne peux écrire l'accélération telle que tu l'as posée que si la vitesse de rotation est constante. Or ici on en est très loin

Pour te convaincre   tu te rends à "vitesse et accélération en coordonnées polaires"

Posté par
diracre : 2 équations différentielles du mouvement 20-12-19 à 20:45

Nous en étions donc à:

1/ donner les expressions des vitesse et accélération dans le repère mobile

\vec{v} = \dot{\rho}\vec{e}_\rho + \rho\dot{\theta}\vec{e}_\theta

\vec{a} = (\ddot{\rho}-\rho\dot{\theta}^2)\vec{e}_\rho + (2\dot{\rho}\dot{\theta}+\rho\ddot{\theta})\vec{e}_\theta

2/ Projeter la RFD dans ce repère

m\vec{a} = \vec{P} +\vec{F}+\vec{R}

avec

\vec{P} = -mg(sin\theta\vec{e}_\rho + cos\theta\vec{e}_\theta)

\vec{F} = -kBM(cos\alpha\vec{e}_\rho + sin\alpha\vec{e}_\theta)

\vec{R} = R.\vec{e}_\rho

Et les propriétés géométriques suivantes:

\alpha = \frac{\pi}{4} - \frac{\theta}{2}    et    BM = 2acos\alpha

Donc en projetant sur les 2 axes du repère mobile

ma\dot{\theta}^2 = mgsin\theta - R + 2kacos^2\alpha  (1)

ma\ddot{\theta} = - mgcos\theta -2kasin\alpha cos\alpha   (2)

3/ Trouver (t)

(2)  peut s'écrire après avoir remarqué que  2sin\alpha cos\alpha = sin2\alpha=cos\theta:

\ddot{\theta} = -cos\theta(\frac{g}{a} + \frac{k}{m} )  (rassurant le k/m   )

On cherche  \theta(t)   de la forme  \theta(t) = \theta_0.cos(\omega t + \phi)

Les conditions initiales conduisent à  

\theta(t) = \frac{\pi}{2}.cos(\omega t)

avec \omega = \sqrt{\frac{g}{a} + \frac{k}{m}}

sauf distraction ou fatigue

Je laisse ouverte la détermination de R afin que dans un temps plus ou moins long, un de tes pairs pose ici la question


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !